вышка

Решение. По свойству скалярного произведения для двух перпен-

r

r

дикулярных векторов (a,b) = 0. Обозначим координаты искомого век-

тора

r

r

r

r

r

x ={x; y; z} и запишем условие перпендикулярности

a

x

и b

x

в координатной форме:

r r

(a, x) = 1 x − 1 y + 3 z = 0,

.

(2.11)

r r

x − 2 y + 5 z = 0.

(b, x) = 3

По условию задачи вектор xr – единичный, т. е. его модуль равен единице:

| xr |=

x2 + y2 + z2 = 1.

(2.12)

x − y + 3z = 0,

x − y + 3z

= 0,

y = 4z,

3x − 2y + 5z = 0,

x − z

= 0,

x = z,

x

2

+ y

2

+ z

2

= 1,

2

+ y

2

+ z

2

= 1,

2

+ y

2

+ z

2

= 1,

x

x

4

,

y = 4z,

y = 4z,

y = ±

3 2

x = z,

x = z,

1

,

x = ±

3

2

+

(4z)

2

+ z

2

= 1,

2

= 1,

1

2

z

18z

z = ±

3

.

2

Таким

образом,

мы

нашли

два

r

=

1

;

4

;

1

и

вектора x1

2

3

− 1

− 4

− 1

3

3

2

2

r

;

;

x2

=

3

2

, удовлетворяющих условиям (2.11) и (2.12). Учи-

3

2

3

2

x образует тупой угол с осью

тывая условие задачи о том, что вектор

Задача 8. Даны вершины пирамиды А(0; 1; –3),

B(–2; 0; 1),

C(1; –5; 0), D(–3; 2; 6). Найти объём пирамиды

и длину её высоты, опущенной на грань ABC .

D

Решение. Выполним схематический чер-

теж пирамиды с вершинами ABCD (рис. 2.3).

h

31

A

C

B

(AB, AC, AD) =

− 2

− 1 4

= −2

− 6 3

+ 1

1 3

+ 4

1 − 6

=

1 − 6 3

1 9

− 3 9

− 3 1

− 3

1 9

ния объема пирамиды, получим:

64

32 .

V =

1

(AB,

AC, AD)

=

=

6

6

3

V =

1 hS h = 3 V ,

(2.13)

3

S

где S – площадь основания ABC, может быть найдена как половина мо-

дуля векторного произведения векторов – сторон AB и AC :

S = 1

AC]

.

[AB,

2

Вычислим векторное произведение AB и AC в координатной форме:

[ AB, AC] =

ir

rj

k

− 2 − 1 4

=

1

− 6

3

r

r

=

− 1 4

r

− 2 4

r

+

− 2

− 1

r

r

− 6 3

i −

1 3

j

1

−

6

k =

21i

+ 10 j

+ 13k .

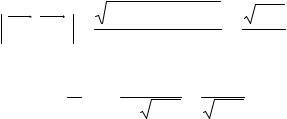
S = 1 [AB, AC] =

212 + 102 + 132

=

710 .

2

2

2

Используя формулу (2.13), находим высоту пирамиды h:

h = 3 V = 3

2 32

=

64 .

S

3

710

710

Задача 9. Относительно некоторого базиса ar,b,cr заданы векторы

er1={2; 1; 3}, er2 ={1; –2; 1}, er3 ={–1; 2; 1}, d ={5; –5; 10}.

а) Докажите, что векторы e1, e2 ,

e3 можно принять за новый базис.

б) Найдите координаты вектора d в базисе { e1, e2 , er3 }.

Решение.

e2 , e3

а) Докажем, что векторы e1,

образуют базис. Для этого доста-

точноустановитьихлинейнуюнезависимость. Поскольку векторы er

,er

,e

r r r

1

2

3

2

1 3

− 1 2

1

1

− 2

0

5

1

~

1 .

− 1

2

0

0

2

1

базисных векторов, т. е.

d = xer1 + yer2 + zer3 .

(2.14)

~

2

1

− 1

|

5

1 − 2

2

| − 5

1 − 2

2

| − 5

1

− 2

2

0

5

− 5

|

0

1

− 1

|

A =

| − 5

~

15

~

3 .

3

1

1

|

10

0

2

0

|

10

0

1

0

|

5

Определитель третьего порядка

1

− 2

2

0

1

− 1

= 1 ≠ 0

0

1

0

2. Даны три прямые l1 :8x − 2 y + 3 = 0 ;

l2

x − 1

=

y + 4

и

l3

x = t − 4,

:

:

1

− 4

y = 4t + 1.

Исследовать взаимное расположение прямых l1

и l2 ; l1

и l3 . Для каждой

а) x 2 + y2 − 8x = 0;

б) x = −

1

25 − y2 ;

3

в) –2 x 2 + 3 y2 − 4x + 15y + 4 = 0;

г) x + 4y − 2y 2 − 5 = 0.

а) x = − cos t,

б) x = (t3 − t) / 4,

y = 3sin t;

y = t 2 / 2.

6. Составить уравнения плоскостей, которые проходят:

а) через три точки A(5; –1; 1), B(0; –2; 1), C(1; –3; 0);

б) через точку A(5; –1; 1) перпендикулярно прямой

x

=

y − 4

=

z + 4

;

3

r

−1

4

в) через точку B(0; –2; 1) параллельно двум векторам a1

= {0;−1;2} и

ar2 = {1;2;−1};

x − y + 7z = 0,

д) заданной в общем виде

= 0.

− 3x + y + 2z + 11

x

y + 1

z − 4

8. Найти точку пересечения и угол между прямой

=

=

и

1

− 1

плоскостью x − 5z + 1 = 0 .

3

9. Определить тип и построить поверхности

а) x2 + 4 y2 + 4x − z2 + 2z = 0 ;

б) y2 − 2 y + z2 = 0 .

Название уравне-

Аналитический вид

Входящие постоянные

ния прямой l

Общее в коорди-

A(x − x )+ B(y − y

0

) = 0

N = {A; B},

натной форме

0

M 0 ( x0 ; y0 ) l ,

Nr l

Общее

Ax + By + D = 0

N = {A; B}, Nr

l

В отрезках

x

+

y

= 1

a и b – это отрезки, отсе-

a

b

каемые от Ox и Oy

Параметрическое

x = t m

+ x0

M 0 (x0 ; y0 ) l , σ = {m;n},

σ || l , t

– параметр

y = t n + y0

x − x

0

y − y

0

M 0 (x0 ; y0 ) l ,

r

Каноническое

=

σ = {m; n}

m

n

По двум точкам

x − x0

=

y − y0

M 0 (x0 ; y0 ) l ,

y1 − y0

M

(x ; y ) l

x1 − x0

1

1

1

С угловым коэф-

y = kx + b

k =

n

,

b = y

−

n

x

фициентом

0

m

0

m

Таблица 3.2

Различные формы уравнения прямой в пространстве

Название

уравне-

Аналитический вид

Входящие постоянные

ния прямой l

x

= t m + x0

M

0

(x

0

; y

0

; z

) l ,

Параметрическое

= t n + y0

0r

y

σ = {m;n; p}, σ || l ,

z = t p + z0

t – параметр

Каноническое

x − x0

=

y − y0

=

z − z0

M 0 (x0 ; y0 ) l ,

m

p

n

σ = {m;n; p}

По двум точкам

x − x0

=

y − y0

=

z − z0

M 0 (x0 ; y0 ; z0 ) l ,

y1 − y0

z1 − z0

x1 − x0

M1 (x1; y1; z1 ) l

Различные формы уравнения плоскости

Таблица 3.3

Название

Аналитический вид

Входящие

уравнения плос-

постоянные

кости L

Общее в коор-

A(x − x0 )+ B(y − y0 )+ C(z − z0 ) = 0

M 0 (x0 ; y0 ; z0 ) L ,

динатной форме

N = {A; B;C}, Nr

L .

Общее

Ax + By + Cz + D = 0

N = {A; B;C}, Nr

L .

x

+

y

+

z

= 1

a, b, с – это отрезки,

В отрезках

отсекаемые от Ox,

a

b

c

Oy, Oz.

x − x0

y − y0

z − z0

M 0 (x0 ; y0 ; z0 ) L,

По трем точкам

x1

− x0 y1

− y0 z1

− z0

= 0

M1 (x1; y1; z1 ) L,

x2

− x0 y2

− y0 z2

− z0

M 2 (x2 ; y2 ; z2 ) L.

Кривые 2-го порядка

Таблица 3.4

Название

Аналитический вид

Графическое

кривой

изображение

(x − x )2 + (y − y

0

)2 = r2

0

M0

r

Окружность

M0(x0;y0) – центр окружности,

y0

r – радиус

x0

(x − x )2

(y − y )2

b

0

+

0

= 1

Эллипс

a2

b2

y0

M0

a

M0(x0;y0) – центр окружности,

x0

a, b – полуоси

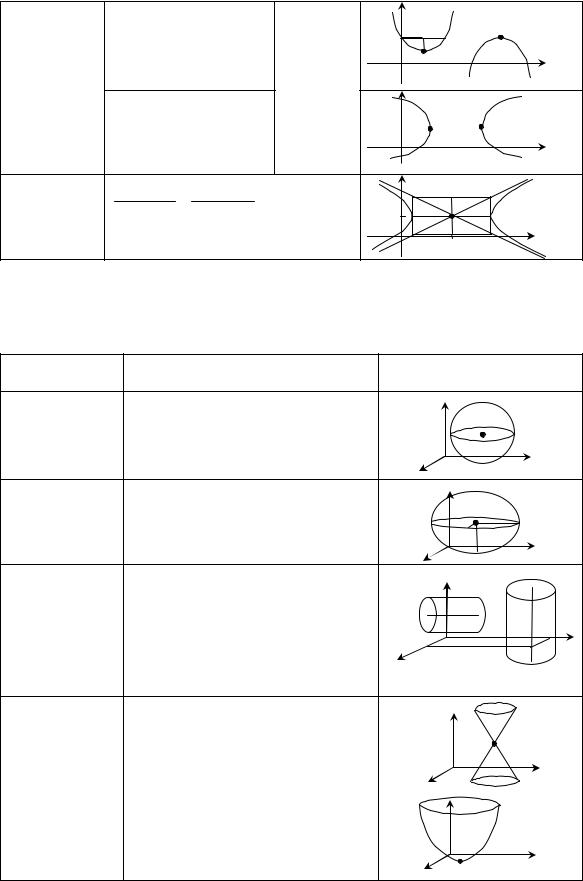
(x − x0 )2 = 2 p(y − y0 )

M0(x0;y0) –

p p/2

M0

вершина

M0

p<0

Парабола

параболы,

p>0

p – фо-

( y − y

)2

= 2 p(x − x )

кальный

0

0

параметр

M0

M0

p<0

p>0

(x − x0 )2

−

(y − y0 )2

= 1

b

a

Гипербола

a2

b2

y0

M0(x0;y0) – центр гиперболы,

M0

x0

a, b – полуоси

Поверхности 2-го порядка

Таблица 3.5

Название

Аналитический вид

Графическое

поверхности

изображение

(x − x0)2 + (y − y0)2 + (z − z0)2 = r2

z

Сфера

M0(x0;y0;z0) – центр сферы,

M0

r – радиус

x

y

(x − x )2

+

(y − y )2

+

(z − z )2

= 1

z

2

2

2

M0

a

0

b

0

c

0

Эллипсоид

a

b

M0(x0;y0;z0) – центр эллипсоида,

c

y

a, b, с – полуоси

x

a)

(x − x )2

+

(z − z )2

= 1

z

0

0

l

a2

b2

l

Цилиндр

Ось l | | Oy.

x x0

y0

(x − x0 )2

( y − y0 )2

b)

+

= 1

y

a2

b2

a)

b)

Ось l | | Oz.

(x − x )2

+ (y − y )2

= (z − z )2

z

Конус

0

0

0

M0

M0(x0;y0) – вершина конуса

x

y

z

Эллиптический

(x − x )2

+ (y − y )2

= 2p(z − z )

p>0

параболоид

0

0

0

y

x

M0

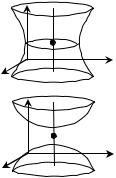
Гиперболоид

z

(x − x )2

(y − y )2

(z − z )2

M0

(однополост-

0

+

0

−

0

= 1