Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Гусев_сопротивление_материалов

.pdf

Скачиваний:

Добавлен:

03.05.2015

Размер:

4.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ

Задание 18

Дана прямоугольная полоса (рис.18.1) длиной l, высотой h и толщиной, равной единице. Начало координат О взято в центре тяжести площади левого сечения. Оси Oy и Оz являются осями симметрии сечения. Ось Ох проходит вдоль осевой линии полосы. Задана функция напряжений (x,y) (табл.18).

Рис.18.1

Требуется:

1)Проверить, удовлетворяет ли заданная функция напряжений θ(x,y) дифференциальным уравнениям плоской задачи теории упругости.

2)Определить компоненты напряжений распределения.

3)Построить эпюры напряжений ζx, ζy и ηxy в сечении с координатой х.

4)Найти внешние силы (нормальные и касательные), действующие вдоль линии контура полосы. Построить графики их

Таблица 18

Номер строки	Функция напряжений (x, y)
0	=a(x4-y4)+bx3y+xy3
1	=ax(x2+y2)+bx2y+xy
2	=ay(x2+y2)+bxy2+xy
3	=ax3+bx2y+xy2+xy
4	=a(y4-x4)+bxy3+x2y
5	=ax4-3ax2y2+bxy3
6	=ax3y-3bx2y2+by4
7	=ax4-3(a+b)x2y2+by4
8	=axy3+x3+y3+bxy
9				1
	3	2	2	1	4
	=ax	y+b(x y		-	y	)
	=ax	y+b(x y		-	y	)
				3
	81

								Таблица 18а

Номер схемы	a		b	l	h		x	y
		МПа/м				м
0	1		1	5	1		1	0,2
1	2		1	6	1		2	0,3
2	2		1	5	2		2	0,4
3	1		2	6	1		2	0,3
4	1		2	6	2		2	0,5
5	2		2	4	2		1	0,5
6	2		1	4	2		1	0,5
7	2		1	6	1		3	0,3
8	1		2	5	1		2	0,2
9	2		1	5	2		2	0,4

Пример 18

Даны размеры полосы l = 2 м, h = 1 м, координата x=1м. Задана

функция напряжений θ(x, y) = ax3y – 3bx2y2+ by4, где а = 2 МПа/м, b = 1 МПа/м2.

Решение:

1. Воспользуемся дифференциальным уравнением плоской задачи теории упругости

д4

0 .

дx2дy2

дy4

дх4

Дифференцируем функцию напряжений:

= 3ах2y – 6bxy2;

д2

= 6ахy – 6by2;

д3

= 6аy;

д4

= 0;

дх

дх2

дх3

дх4

= 3ах3 – 6bx2y + 4by3;

д2

= 6bх2

+ 12by2;

д3

= 24by;

д4

= 24b;

дy

дy2

дy3

дy4

д2

= 3аx2 – 12bxy;

д3

= 6ах – 12by;

д4

= - 12b;

дх2дy2

дхдy

дх2дy

Полученные производные подставляем в дифференциальное уравнение. Получим 0 + 2(-12b) + 24b = 0 или 0 = 0. Следовательно, функция θ(x,y) тождественно удовлетворяет дифференциальному уравнению плоской задачи теории упругости.

2. Определяем компоненты напряжений:

д2

6bx2

+ 12by2;

д2

6axy - 6by2;

дy2

дx2

д2

- 3ax2 + 12bxy.

дхдy

3. Находим распределение напряжений

в сечении

координатой

х = 1 м. Для этого в

выражения ζx, ζy и ηxy

подставляем

х = 1 м, а =

2 МПа/м и b = 1 МПа/м2. Находим

ζx = 6 + 12y2;

ζy = 12y – 6y2;

ηxy = -6 + 12y.

Изменяя y от

до

(от –0,5 м до +0,5 м), вычисляем напряжения

и строим эпюры (рис. 18.2).

4. Определяем внешние силы,

действующие на контуре (на гра-

нях) полосы. Для этого восполь-

зуемся граничными условиями:

Рxv = ζx cos(x, v) + ηxy cos(y, v),

Рyv = ηxy cos(x, v) + ζy cos(y, v),

Рис. 18.2

где Рxv, Рyv - проекции внешних сил

на оси координат Ох и Oy; ν – нор-

маль к линии контура; cos(x, v),

cos(y, v) - направляющие косинусы нормали.

Верхняя грань: y =

= 0,5 м;

ζx = 6bx2 + 12by2 = 6x2 + 3;

ζy = 6axy – 6by2 = 6x – 1,5; ηxy = - 3ax2 + 12bxy = -6x2 + 6x;

l = cos(x, v) = cos(x, y) = = 0;

m = cos(y, v) = cos(y, y) = 1;

Рxv = ζx·0 + ηxy· 1= -6x2 + 6x;

Рyv = ηxy·0 + ζy 1 = ζy = 6x – 1,5.

Изменяя х от 0 до 2 м, вычисляем нормальную Рyv и касательную Рxv

составляющие, строим графики (рис.18.3).

Нижняя грань: y = -

= - 0,5 м;

ζx = 6x2 + 3;

ζy = - 6x – 1,5;

ηxy = - 6x2 - 6x;	l = cos(x, v) = cos(x, y) = 0; m = cos(y, v) = cos(y, -y) = -1;
Рxv = ζx·0 + ηxy· (-1) = - ηxy = 6x2 - 6x; Рyv = ηxy·0 + ζy (-1) = - ζy = -6x .+ 1,5.
Изменяя х от 0	до 2 м, вычисляем нормальную Рyv и касательную Рxv

составляющие, строим графики (рис.18.3).

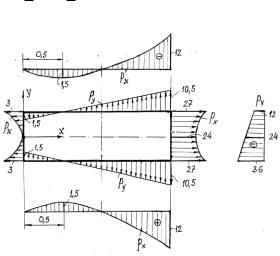
Левая грань: х = 0;					ζx = 12y2;	ζy = - 6y2; ηxy = 0;
l = cos(x, v) = = cos(x, -x) = -1; m = cos(y, v) = cos(y, -x) = 0;
Рxv = ζx·(-1) + ηxy·0 = - ζx = = -12y2;						Рyv = ηxy·(-1) + ζy 0= - ηxy = 0.
Изменяя y от	h	до		h	(от –0,5 м до +0,5 м), вычисляем нормальную
2			2

Рxv и касательную Рyv составляющие, строим графики (рис.18.3).

Правая грань: х=l=2 м; ζx = 24 + 12y2; ζy = 24y - 6y2; ηxy = -24 + 24y; l = cos(x, v) = cos(x, x) = 1; m = cos(y, v) = cos(y, v) = 0;

Рxv = ζx·1 + ηxy·0 = ζx = 24 + 12y2; Рyv = ηxy· 1 + ζy 0= ηxy = -24 + 24y.

Изменяя y от h2 до h2 ( от –0,5 м до +0,5 м), вычисляем нормальную

Рxv и касательную Рyv составляющие, строим графики (рис.18.3).

Рис. 18.3

ИЗГИБ ПЛАСТИНКИ

Задание 19

Дана прямоугольная пластинка (рис.19.1) под действием поперечной внешней нагрузки интенсивности q(x,y). Задано уравнение изогнутой поверхности пластинки w(x,y) (табл. 19). Известны размеры сторон a, b и толщина стенки h.

Рис. 19.1

Требуется:

1.Определить условия закрепления пластинки по линии контура (граничные условия).

2.Найти коэффициент С.

3.Построить эпюры изгибающих моментов Mx, My, крутящих моментов Mxy и поперечных сил Qx, Qy для сечения с координатами x и y.

Считать жесткость пластинки на изгиб (цилиндрическую жѐсткость) D = const. Числовые данные взять из табл. 19а.

Таблица 19

Номер строки

Уравнения поперечной нагрузки q(x,y) и

изогнутой поверхности w(x,y)

q q sin x cos

; w C sin x cos y

q q0 cos

sin

; w C cos

sin

q q sin

2 x

cos

; w C sin

2 x

cos

q q0 cos

x sin

2 y

; w C cos x sin

2 y

q = const; w = C (x2-a2)(y-b)2

окончание таблицы 19

	5					q = const; w = C (x-a)2(y2-b2)
	6					Q = const; w = C (x2-a2)(y2-b2)
	7			q q0 cos								x			cos			y	; w	C cos	x		cos			y
												x						y			x					y
																		2b								2b
												2a						2b			2a					2b
	8		q q0 cos						3 x				cos			3 y			; w	C cos	3 x				cos			3 y
									3 x							3 y					3 x							3 y
																												2b
										2a							2b				2a							2b
	9		q q0 cos								3 x			cos			y		; w	C cos	3 x			cos			y
											3 x						y				3 x						y
																		2b										2b
											2a							2b			2a							2b
																							Таблица 19а

Номер схемы		a	b			h											x			y
Номер схемы						м
						м
0		4	3		0,1												3			2		0,35
1		3	3		0,1												2			2		0,3
2		3	3		0,1												1			1		0,25
3		4	4		0,2												2			3		0,25
4		5	3		0,1												3			1		0,3
5		3	5		0,1												1			3		0,3
6		3	3		0,2												2			2		0,35
7		5	5		0,2												2			2		0,35
8		5	4		0,2												3			1		0,3
9		4	5		0,2												2			3		0,3
				Пример 19
Интенсивность поперечной нагрузки
		q = q0 cos	x	cos		3 y		;				q0 = const.														(19.1)
			2a			2b
Уравнение изогнутой поверхности пластинки
		w = C cos	x	cos	3 y		.																				(19.2)
		w = C cos		cos			.																				(19.2)
			2a			2b

Здесь q(x,y) – нагрузка на единицу площади поверхности; a = 2 м и b = 1 м – размеры сторон; μ = 0,3 – коэффициент Пуассона. Координата

y b6 .

Решение:

1. Для определения граничных условий по линии контура пластинки воспользуемся уравнением изогнутой поверхности (19.2). Очевидно, что при х = ± а, w = 0 и при y = ± b, w = 0. Получается, что прогибы по линии контура пластинки равны нулю.

Уточняем схему закрепления пластинки: шарнир или заделка. Дифференцируя функцию (19.2) по координате x, получим уравнение углов поворота нормали в направлении оси Ох:

дw

= - C

sin

cos

3 y

дх

Очевидно, при х=-а,

дw

cos

3 y

; при х=+а,

дw

= -C

cos

3 y

дх

Углы поворота нормали не равны нулю. Это значит, что левый и правый края пластинки закреплены шарнирно.

Дифференцируя функцию (19.2) по координате y, получим уравне-

ние углов поворота нормали в направлении оси Oy:

дw

= - C

sin

3 y

cos x .

дy

Очевидно, при y = -b,

дw

= C

cos x ; при y =+b,

дw

=-C

cos

x .

дy

Таким образом, верхний и нижний края пластинки также шарнирно закреплены. Пластинка шарнирно опѐрта по линии контура.

2. Для определения коэффициента С воспользуемся дифференциальным уравнением изгиба пластин:

q x, y .

дx

дy

Находим производные:

д2w

3 y

cos

;

дx2

д3w

3 y

sin

cos

;

дx3

д4w

3 y

cos

;

дx4

д2w

sin

3 y

;

дxдy

2а 2b

д3w

cos

sin

3 y

;

дyдx2

д3w

3 2

3 y

sin

cos

;

(19.4)

дxдy2

2а

д4w

3 2

3 y

cos

;

дy2дx2

д2w

3 y

cos

;

дy2

д3w

3 y

cos

sin

;

дy3

д4w

3 y

cos

дy4

Производные (19.4) и заданную функцию q (x, y) подставляем в дифференциальное уравнение (19.3). После преобразований получим

C			q0				.
C			2	3	2	2	.
				3
	D
	D

		2a		2b

3.Записываем выражения для изгибающих моментов

, M y D

;

M x D

дx

дy

дx

крутящих моментов

M xy D 1 ддx2дwy ;

и поперечных сил:

	3	w	3	w
	д	w	д	w		,
Qx D		3			2	,
		3	дхдy		2
	дx		дхдy

	д3w		д3w
Qy D				.
		3	2
	дy
			дyдx

Подставляя в эти выражения производные (19.4), находим

q0 cos

cos

3 y

;

q0 cos

x cos

3 y

;

2 2

1 sin

3 y

M xy

sin

;

q0 sin x cos

3 y

;

q0 cos x sin

3 y

выражения

усилий

подставляем

координату y

исходные

данные. Находим:

M x

0,1

cos

; M y

0,3

cos

;

M xy 0,035

sin

;

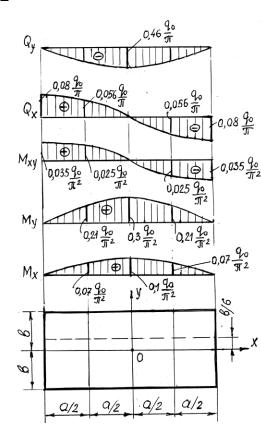
Qx 0,08	q0	sin	x	;	Qy 0,46	q0	cos	x .
			2a
								2a
Полученные выражения		определяют распределения усилий в

сечении y b6 . Изменяя х от – а до + а, строим эпюры (рис. 19.2).

Рис. 19.2

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.2019215.67 Кб18Гражданкие здания.docx
#
03.05.2015185.12 Кб352График документооборота,12, приложение 1.rtf
#
22.11.201947.34 Кб18Графология.docx
#
17.09.2019237.05 Кб8ГРЭ!!!.docx
#
21.12.2018118.78 Кб6Гульельмо Марко́ни2.doc
#
03.05.20154.54 Mб92Гусев_сопротивление_материалов.pdf
#
03.05.201533.93 Кб95деловое общение в Англии.docx
#
25.12.20183.4 Mб6дима электротехника.doc
#
03.05.20151.9 Mб193ДИПЛОМ 1 (Восстановлен).docx
#
27.09.20198.82 Mб8ДИПЛОМ ОСНОВНОЙ !!!!!!!!!.docx
#
03.05.2015226.8 Кб9диплом продолжение 1.docx