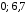05-01

!Taskfile kontr_СМ 2-05-01#Статические моменты. Центр тяжести плоской фигуры

!De=kontr_СМ 2-05#Геометрические характеристики поперечных сечений стержня

!Task1

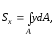
Интегралы называются …

!Solution

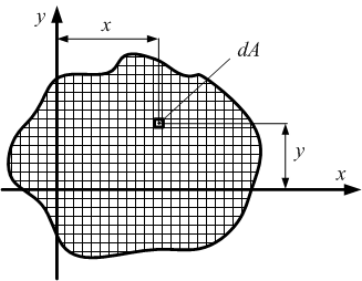
Рассмотрим некоторую плоскую фигуру (см. рисунок). Отнесем ее к системе координат x, y. Разобьем площадь фигуры на элементарные площади прямоугольной координатной сеткой. Если каждую элементарную площадь помножить на координату y ее центра тяжести и сложить все произведения, то получим статический момент площади относительно оси x. Чем меньше шаг сетки, тем точнее результат. Заменяя суммирование интегрированием по площади, получаем 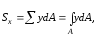где А – площадь фигуры.

Аналогично определяем статический момент площади сечения относительно оси y:

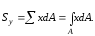
!True

статическими моментами площади плоской фигуры относительно координатных осей x и y

!Task3

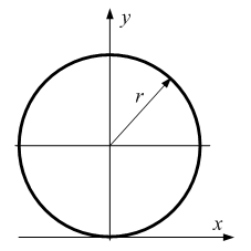
Статический момент площади круга относительно оси x равен …

!Solution

Статический момент площади фигуры относительно оси x .

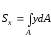В данном случае

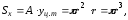
где А – площадь круга,

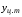– координата центра тяжести.

!True

!Task4

Статический момент площади сечения относительно оси y равен …

!Solution

Статический момент сечения относительно оси y .

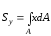В данном случае ,

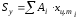где А_i – площади составляющих фигур,

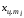– абсциссы центров тяжести составляющих фигур.

.

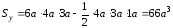!True

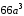
!Task5

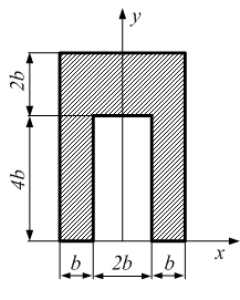
Координаты центра тяжести фигуры равны …

!Solution

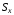Центр тяжести располагается в точке на оси симметрии, поэтому его координата по оси x . Координату по оси y определим по формуле где − статический момент площади относительно оси x, А – площадь фигуры.

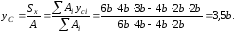
!True

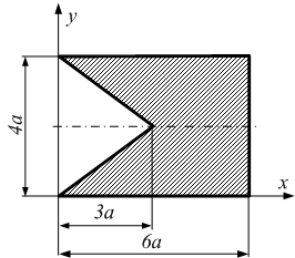
!Task7

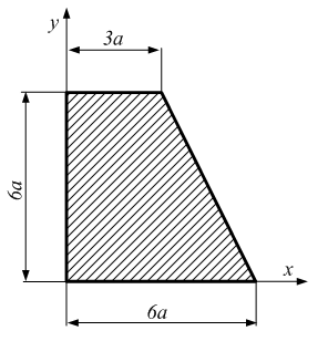
Координаты центра тяжести трапеции (см. рис.) в заданной системе координат

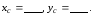
!Solution

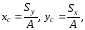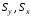Разобьем сложную фигуру на простые фигуры, площади которых можно вычислить и положения центров тяжести которых известны. В данном случае это прямоугольник и треугольник. Координаты центра тяжести трапеции определим по формулам где − статические моменты площади трапеции относительно осей y и x, А – площадь трапеции.

Подставляя найденные значения 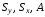в формулы для определения 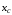и получаем

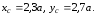
!True

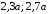
!Task8

Сечение состоит из двутавра и швеллера. В системе координат 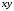координаты центра тяжести фигуры

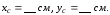
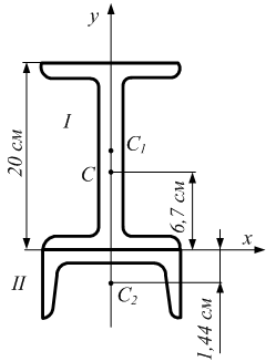
Точки C₁ и C₂ – центры тяжести поперечных сечений двутавра и швеллера. Из ГОСТов возьмем геометрические характеристики двутавра №20 и швеллера №10. Положение центра тяжести сечения определим в системе координатных осей x и y. Центр тяжести сечения расположен на оси симметрии (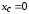). Координату центра тяжести сечения по оси 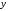определяем по формуле 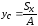, где

– статический момент фигуры относительно оси x;

А – площадь фигуры.

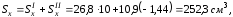
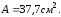
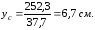
!True