Вариант 8.

1. Упростить и вычислить определитель.

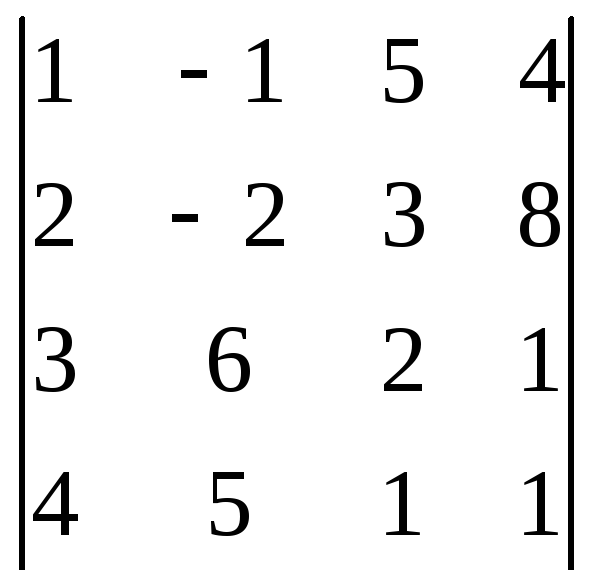
2. Решить матричным методом.

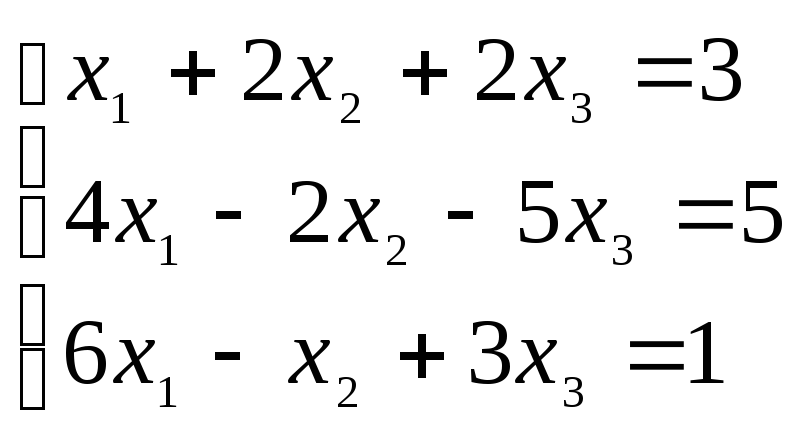
3. Решить систему методом Гаусса

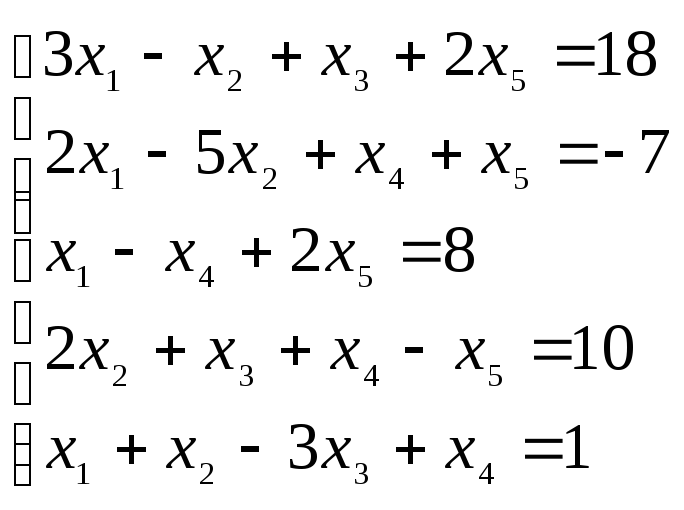
4. При каком значении  векторы и, будут взаимно перпендикулярны, если,, угол.

5. Найти вектор , зная, что он перпендикулярен векторам и , а его проекция на вектор равна 5.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (10,-1), B (-2,-6). C (-6,-3)

7. Найти координаты центра окружности, описанной около треугольника с вершинами А(-1,1), B(2, -1), C(4,0).

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (6,1,1); В (4,6,6); С (4,2,0); D (1,2,6)

Вариант 9.

1. Упростить и вычислить определитель.

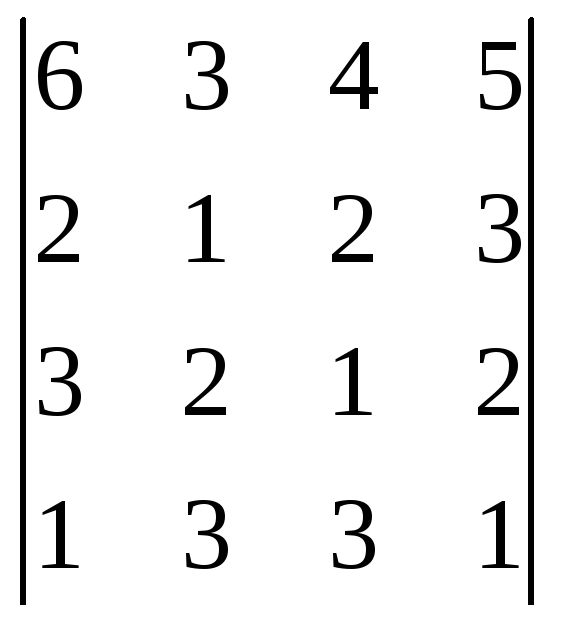
2. Решить матричным методом

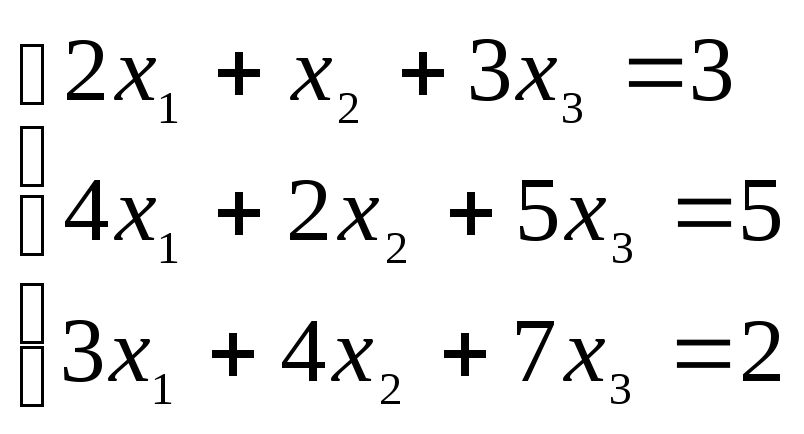
3. Решить систему методом Гаусса

4. Найти проекцию вектора на вектор, еслии- единичные векторы и.

5. Убедиться, что диагонали параллелограмма, построенного на векторах икак на сторонах, взаимно перпендикулярны.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (0,5), B (12,0), C (18,8)

7. Дана сторона треугольника АВ: и уравнения двух высотАD: иBE: . Найти уравнение третьей высоты.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (7,5,3); В (9,4,4); С (4,5,7); D (7,9,6)

Вариант 10.

1. Упростить и вычислить определитель.

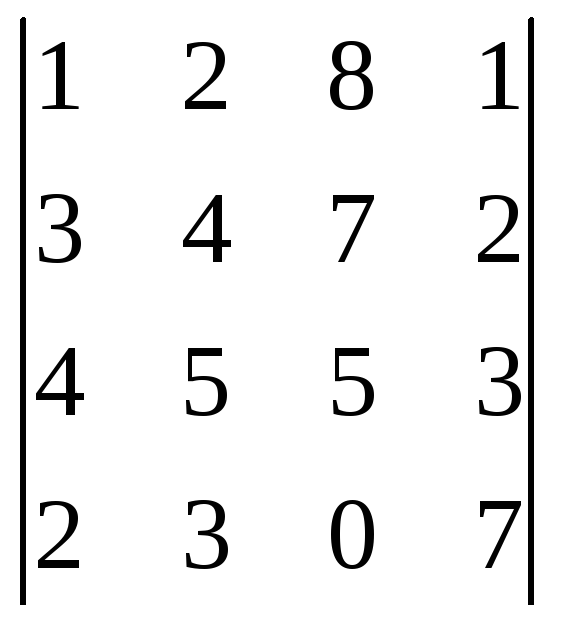
2. Решить матричным методом.

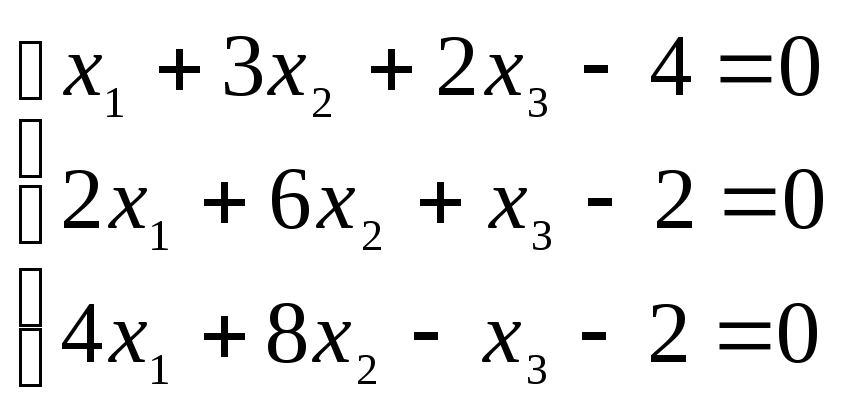
3. Решить систему методом Гаусса

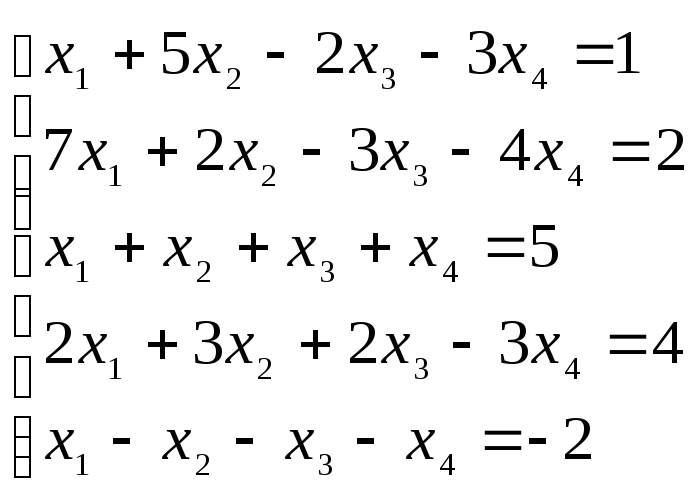
4. Определить длину диагоналей параллелограмма, построенного на векторах и, если,,.

5. Какой угол образуют векторы и, если и .

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (-12,6), B (12,-1), С (-6,23)

7. Высоты треугольника ABC пересекаются в точке Н(2,1), стороны заданы уравнениями АВ: ,ВС: . Найти уравнение стороныАС.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (6,6,2); В (5,4,7); С (2,4,7); D (7,3,0)

Вариант 11.

1. Упростить и вычислить определитель.

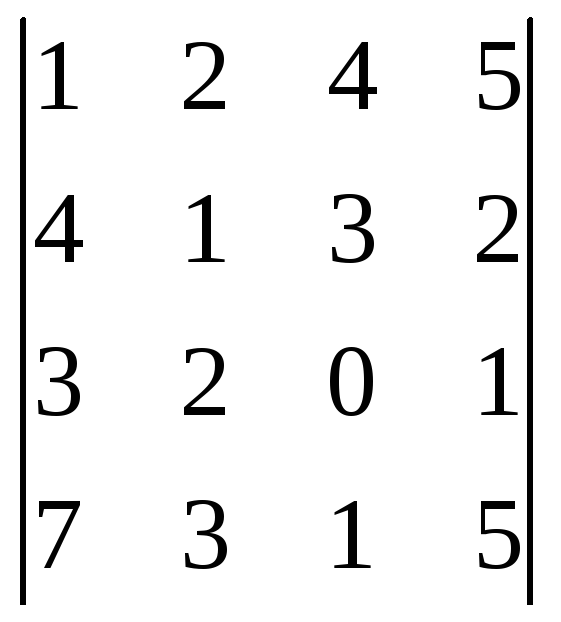
2. Решить матричным методом.

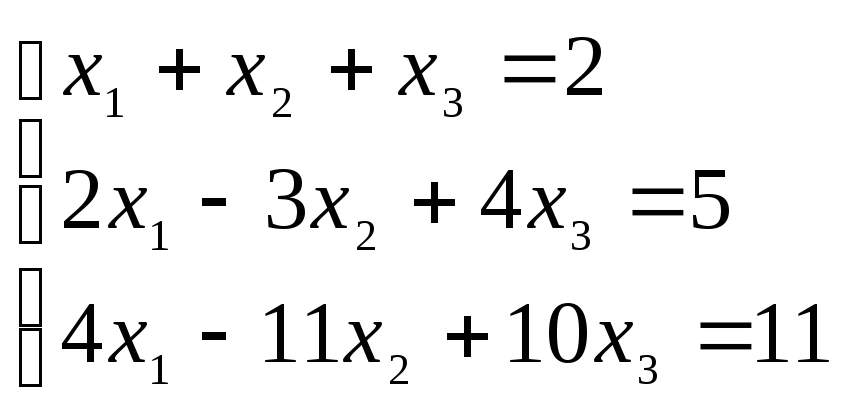
3. Решить систему методом Гаусса

4. Даны векторы ,,, причем,,, углы,. Найти длину вектора.

5. Даны векторы , и . Найти проекцию вектора на вектор .

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (3,0), B (-4,2), C (-8,-2)

7. Дан треугольник с вершинами А(6,4), B(-3, 5), С(-2,-6). Най­ти прямую, проходящую через точку А параллельно медиане, проведенной через точку В.

8. . Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (4,0,0); В (-2,1,2); С (1,3,2); D (3,2,7)