Вариант 4.

1. Упростить и вычислить определитель.

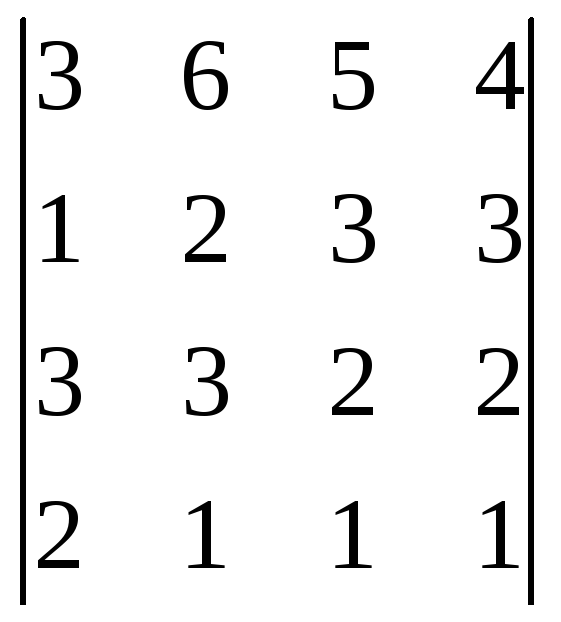
2. Решить матричным методом.

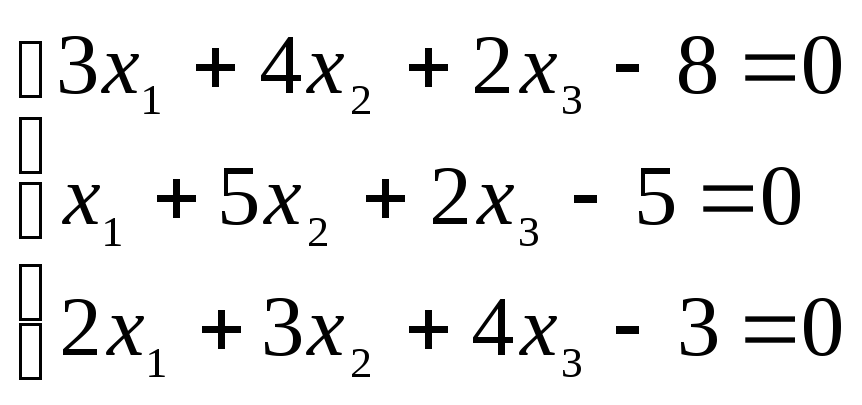
3. Решить систему методом Гаусса

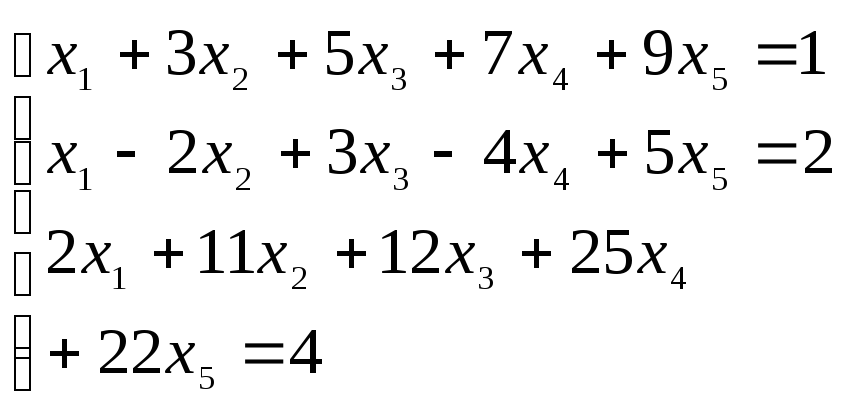
4. Найти длину диагоналей параллелограмма, построенного на векторах и, если,, угол.

5. Найти вектор , коллинеарный вектору и удовлетворяющий условию .

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (1,1), B (-15, 11), С (-3,13)

7. Даны уравнения сторон параллелограмма и, и одна из его вершинС(4,-1). Составить уравнения двух других сторон.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (2,4,3); В (7,6,3); С (4,9,3); D (3,6,7)

Вариант 5.

1. Упростить и вычислить определитель.

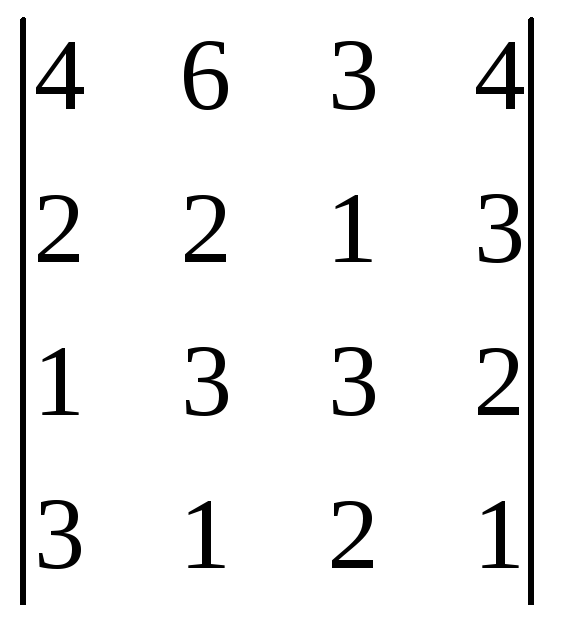
2 Решить матричным методом.

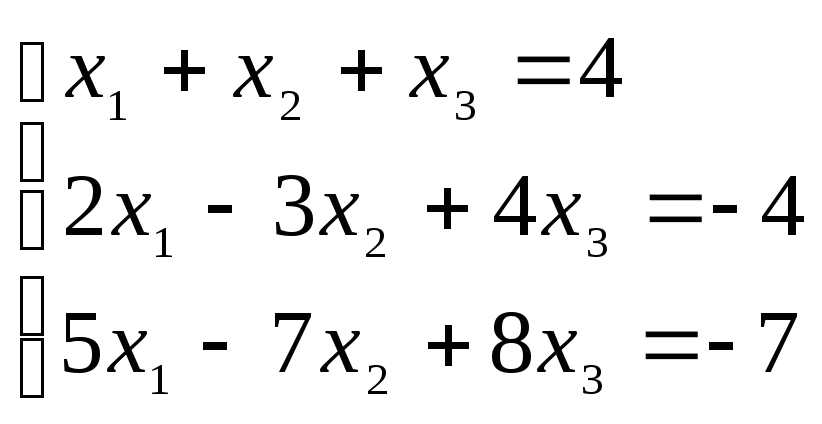
3. Решить систему методом Гаусса

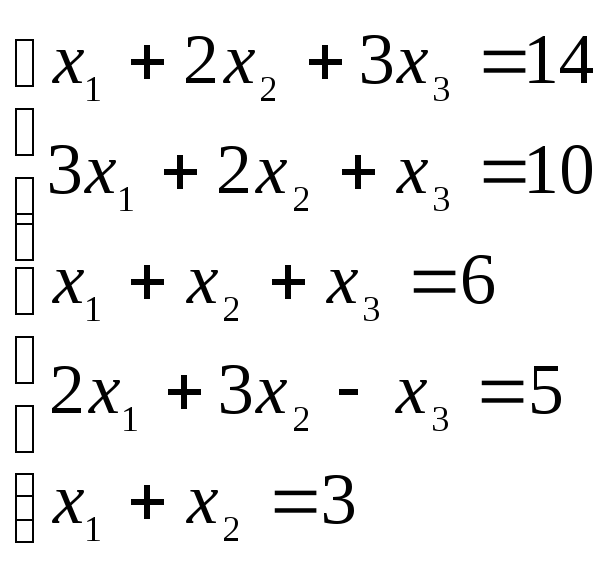
4. Известно, что ,. Чему равен угол между векторамии, если.

5. Вектор , лежащий в плоскостиXOZ, перпендикулярен вектору . Найти его координаты, если.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (-14,10), B (10,3), С (-8,27)

7. Даны вершины треугольника А(3,-1), B(4,0) и D(2,1) - точка пересечения медиан. Найти уравнение высоты, проходящей через третью вершину С.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (9,5,5); В (-3,7,1); С (5,7,8); D (6,9,2)

Вариант 6.

1. Упростить и вычислить определитель.

2. Решить матричным методом.

3. Решить систему методом Гаусса

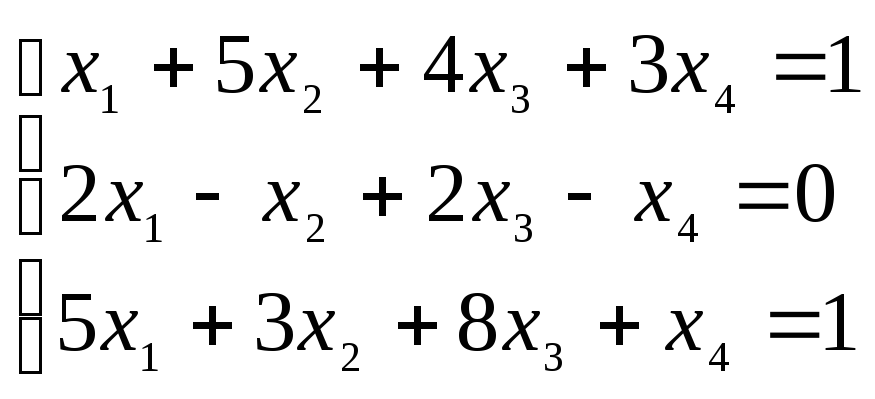
4. Найти длину вектора , если,,,, угол.

5. Найти угол между диагоналями параллелограмма, построенного на векторах и.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (7,1), B (-5,-4), C (-3,-1)

7. Даны уравнения двух сторон параллелограмма ,и точка пересечения его диагоналейР(3,-1). Найти уравнения двух других сторон параллелограмма.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (0,7,1); В (4,1,5); С (4,6,3); D (3,9,8)

Вариант 7.

1. Упростить и вычислить определитель.

2. Решить матричным методом.

3. Решить систему методом Гаусса

4. Найти угол между векторами ,, если,, угол.

5. Найти единичный вектор , перпендикулярный к векторам и .

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (-2,1), B (-13,-11), C (-11,13)

7. Даны вершины треугольника А(16,-15), В(17,-21) и С(0,3). Найти уравнение перпендикуляра, опущенного из точки А на медиану, проведенную из вершины В.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (5,5,4); В (3,8,4); С (3,5,10); D (5,8,2)