58

Министерство образования российской федерации

МАРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ЛИНЕЙНАЯ АЛГЕБРА. ВЕКТОРНАЯ АЛГЕБРА.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Типовой расчет для студентов 1 курса

факультета управления и права

Йошкар-Ола

2004

УДК 51.512;51.514.742.2;51.516 (07)

Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Типовой расчет /Сост. И.С.Антонова, Д.В. Иванов. –Йошкар-Ола: МарГТУ, 2004.-52с.

Приведены 40 вариантов заданий, составленных в соответствии с учебным планом по разделам: «Линейная алгебра», «Векторная алгебра», «Аналитическая геометрия».

Для студентов 1 курса факультета управления и права дневной формы обучения

Печатается по решению

редакционно-издательского совета МарГТУ

Рецензент: заведующий кафедрой математического анализа и теории функции МарГУ, кандидат физ.-мат. наук, доцент В.П. Микка

© МарГТУ, 2004

Вариант 1.

1.Упростить и вычислить определитель.

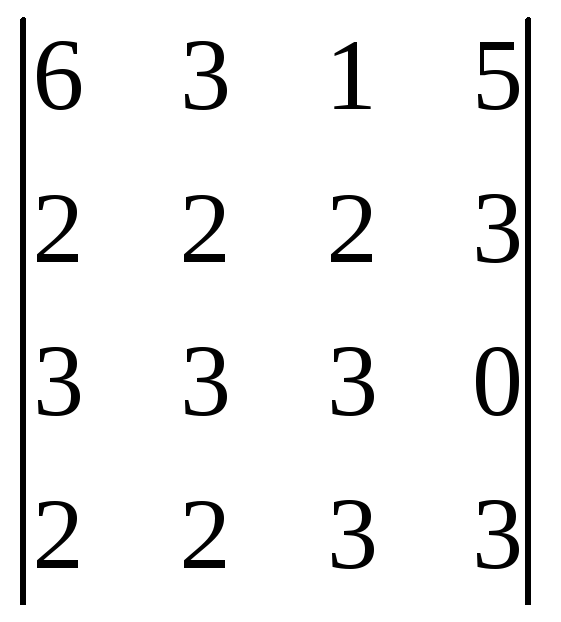
2. Решить матричным методом.

3. Решить систему методом Гаусса

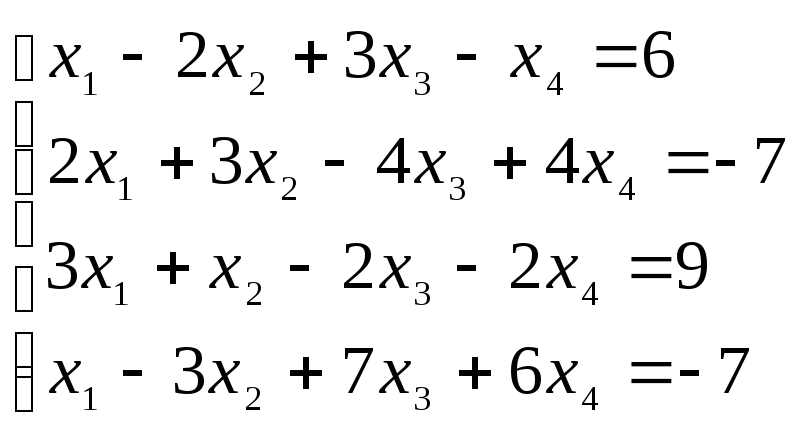
4. Векторы ивзаимно перпендикулярны, векторобразует с ними углы, равные 60. Зная, что ,,, вычислить

5. Найти проекцию вектора на вектор, если , , .

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (6,2), B (30,-5), C (12,19)

7. Даны стороны треугольника и, точкаР(1,2) - точка пересечения третьей стороны с высотой. Найти уравнение третьей стороны.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (3,1,4); В (-1,6,1); С (-1,1,6); D (0,4,-1)

Вариант2

1.Упростить и вычислить определитель

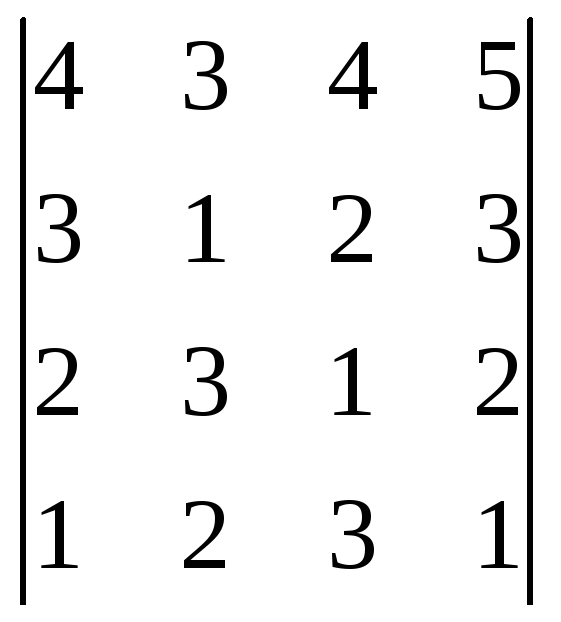
2.Решить матричным методом.

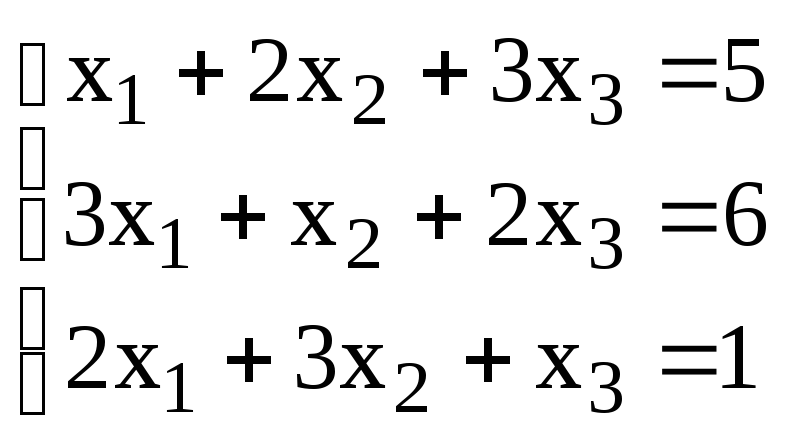
3. Решить систему методом Гаусса

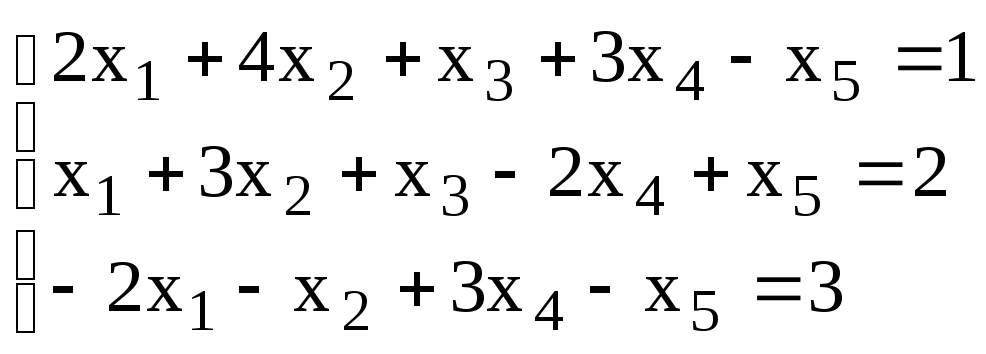
4. Вычислить длину вектора , если,,,, угол между ними.

5. Вектор коллинеарен вектору и образует тупой угол с осью OZ. Зная, что , найти его координаты.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (4,3), B (-12,-9), C (-5,15)

7. Найти точку В, симметричную точке А(-2,4) относительно прямой, проходящей через точки М(1,5) и Р(2,2).

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (3,3,9); В (6,9,1); С (1,7,3); D (8,5,8)

Вариант 3.

1. Упростить и вычислить определитель.

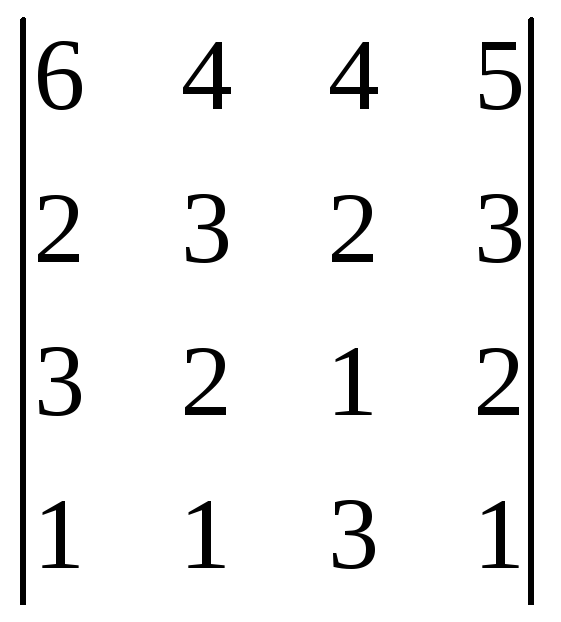
2. Решить матричным методом.

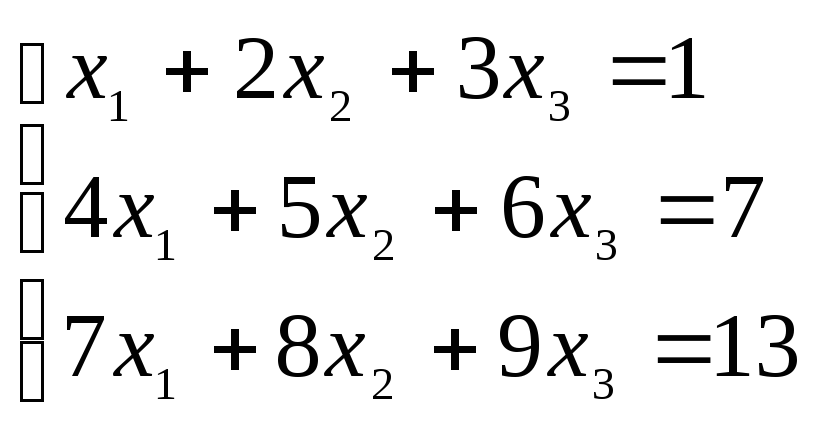
3. Решить систему методом Гаусса

4. Векторы иобразует угол 270°. Зная, что,, вычислить.

5. Вектор образует острый угол с осьюОХ и коллинеарен век­тору , . Найти вектор.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.

A (-1,7), B (11,2), C (17,10)

7. Дан треугольник с вершинами А(-8,3), B(8,5), С(8,-5). Найти точку пересечения его высот.

8. Даны координаты вершин пирамида АВСD. Требуется найти:

1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскости ABC,. Сделать чертеж.

А (3,5,4); В (5,8,3); С (1,9,9); D (6,4,8)