2. Основные случаи съемки

В зависимости от значений угловых элементов внешнего ориентирования снимков , ,  различают различные случаи наземной съемки:

1. Общий случай съемки.

Углы наклона снимков могут принимать произвольные значения (от 0^o до 360^o). На рис. 5.7 показан пример возможной съемки для получения модели пространственного объекта.

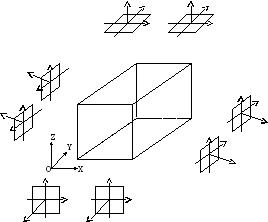
Рис. 5.7

2. Нормальный случай съемки.

В этом случае оптические оси камер параллельны между собой и перпендикулярны базису фотографирования (рис.5.8 или рис.5.9). При этом угловые элементы внешнего ориентирования снимков имеют следующие значения:

₁  ₂  0^o

₁  ₂  90^o

₁  ₁  0^o

Рис. 5.8

Рис. 5.9

3. Равноотклоненный случай съемки.

Оптические оси камер параллельны между собой и отклонены от перпендикуляра к базису на некоторый угол (рис.5.10). Угловые элементы внешнего ориентирования снимков имеют следующие значения:

₁  ₂  

₁  ₂  90^o

₁  ₁  0^o

Рис. 5.10

Этот случай съемки используется для увеличения площади съемки с одного базиса фотографирования. Как правило с одного базиса получают три стереопары.

4. Равнонаклонный случай съемки.

Оптические оси камер параллельны между собой и наклонены относительно горизонтальной плоскости на некоторый угол  (рис.5.11).Угловые элементы внешнего ориентирования снимков имеют следующие значения:

₁  ₂  0^o

₁  ₂  

₁  ₁  0^o

Этот случай съемки применяется когда надо снять высокий объект (например, многоэтажное здание).

Рис. 5.11

5. Конвергентный случай съемки.

Оптические оси камер не параллельны между собой, а повернуты одна относительно другой на некоторый угол , который называется углом конвергентности (рис.5.12). Это позволяет повысить точность определения координат точек объекта за счет увеличения базиса фотографирования и угла засечки. Если угол конвергенции  превышает 16^o, то теряется стереоскопическое восприятие снимков. В этом случае возможны только монокулярные измерения. Поэтому данный случай съемки, как правило, применяется для получения координат маркированных на объекте точек.

Рис.5.12

Особенности фотограмметрической обработки наземных снимков

Все фотограмметрические задачи (прямая, обратная и двойная обратная фотограмметрические засечки) по наземным снимкам решаются по тем же формулам (см. главу 1), что и для аэроснимков.

Особенности фотограмметрической обработки наземных снимков заключаются в том, что в качестве опорной информации кроме опорных точек могут быть использованы координаты центров фотографирования, контрольные направления, превышения между точками, принадлежность точек к одной плоскости, отвесной линии, расстояния между точками и длина базиса фотографирования. Кроме того следует учитывать то обстоятельство, что угловые элементы внешнего ориентирования снимков могут принимать любые значения. В большинстве случаев 90^о

Несколько меняются формулы для прямой фотограмметрической засечки, прямые и обратные формулы связи координат точек местности и снимка для нормального (идеального) случая съемки, за счет того, что =90^о.

Рассмотрим это на примере прямой засечки.

Формулы прямой засечки для общего случая съемки имеют вид ( ):

( )

где

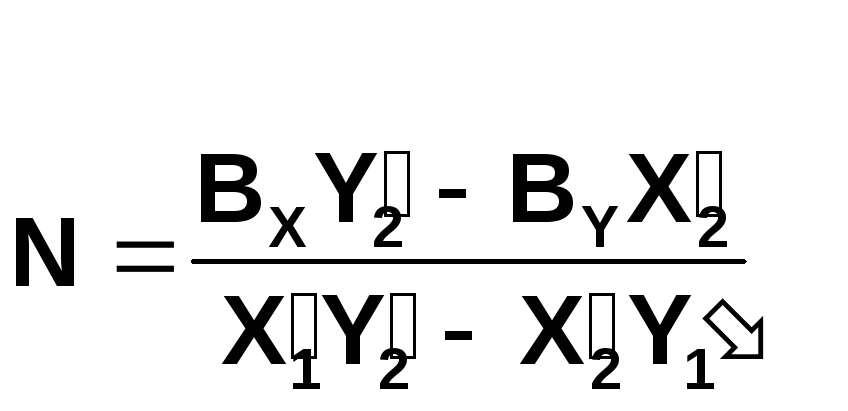
Полагая в этих формулах координаты базиса фотографирования

B равными B_X=B, B_Y=B_Z=O (B – модуль базиса фотографирования ). Кроме того, предположим, что начало системы координат объектаOXYZ совпадает с центром проекции S₁, т.е. и f₁=f₂, а x_0i=y_0i=0. Угловые элементы внешнего ориентирования снимков для нормального случая съемки равны: ₁=₁=₂=₂=0, ₁=₂=90⁰ а соответствующая им матрица поворота:

следовательно

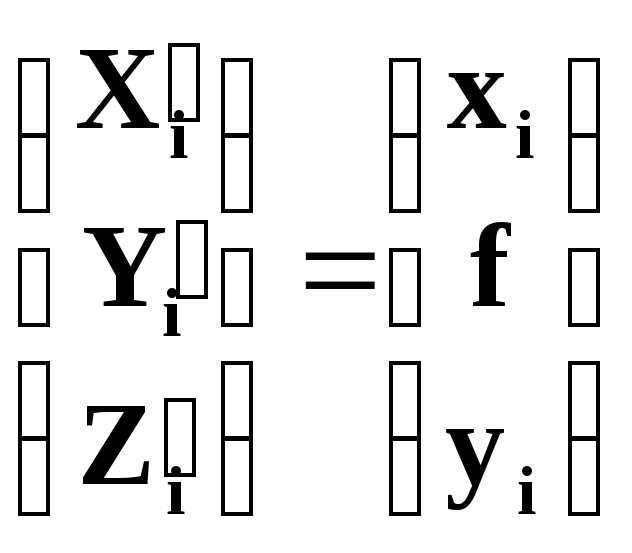
Подставим эти значения в формулу для N:

( )

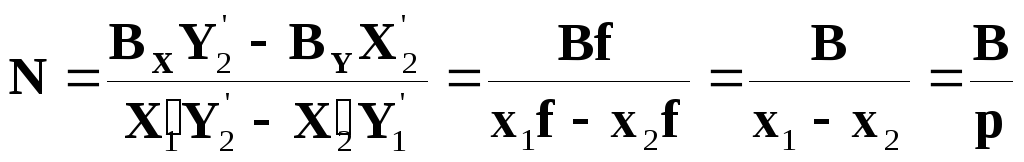Выражения () преобразуются к виду:

( )

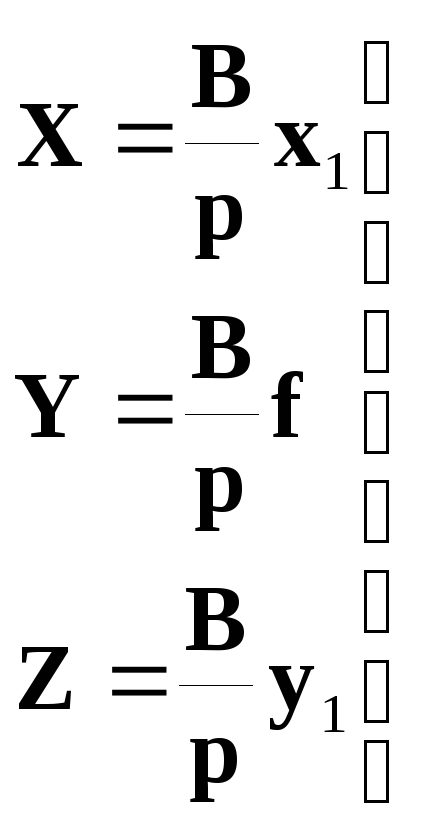Из второго уравнения выражений ( ) получим:

,

тогда формулы ( ) преобразуются в:

( )

Эти формулы используются только для приближенных вычислений.

Если сравнить полученные формулы с соответствующими выражениями, полученными для аэроснимков (), то увидим, что они отличаются только тем, что поменялись Y с Z.