32. Отражение частиц от потенциальной ступеньки. Туннельный эффект.

Так говорит классическая механика

Рассмотрим случай .

Решение ур. Шрёдингера покажет, что происходит с реальными частицами. С учетом того, что в первой области , а во второй , ур. Шредингера для них будет выглядеть так:

Первая область:, Вторая область:

Решения этих уравнений имеет вид , .

Первое слагаемое в описывает падающую волну, второе – отраженную от потенциальной ступеньки. Так как есть решение уравнения и во второй области, то для квантовой частицы имеется конечная вероятность попадания во вторую область. Эта вероятность определяется величиной . Очевидно, что второе слагаемое , растущее с увеличением , должно равняться нулю. Поэтому. Остается первое слагаемое, квадрат которого и определяет конечную вероятность обнаружения частицы за потенциальной ступенькой. Эта вероятность экспоненциально падает с увеличением .

В точке должно выполняться условие непрерывности и , т.е. и .Отсюда получаются формулы, связывающие коэффициенты :

. Таким образом ;

Окончательно волновые функции для первой и второй областей имеют вид:

, . Зайдя во вторую область частица ОБЯЗАТЕЛЬНО вернется.

Перейдем к рассмотрению случая, когда энергия частицы больше высоты ступеньки ().

Ур. Шрёдингера для первой и второй областей выглядит также. С учетом того, что , решения для этих областей теперь имеют вид

, где , .

Оба решения представляют собой суммы падающей и отраженной волн. Так как во второй области нет отраженной волны, то . Для нахождения связи коэффициентов воспользуемся снова условиями непрерывности функции и ее первой производной в точке . Первое условие дает , из второго условия следует , из этих уравнений находим

, .

Мы получили, что коэффициент , определяющий амплитуду отраженной волны, отличен от нуля. Это означает, что при имеется конечная вероятность отражения частиц от барьера. Это чисто квантово-механический эффект, связанный с проявлением волновых свойств частиц.

Определим для потенциальной ступеньки коэффициенты отражения R и прохождения Т. Пусть на ступеньку из первой области падает пучок частиц. Скорость частиц в первой области связана с их импульсом: . Частицы, прошедшие во вторую область, будут иметь скорость . Итак, имеется 3 потока: падающих частиц интенсивностью , отраженных частиц интенсивностью и прошедших интенсивностью

Коэффициент отражения определим как отношение интенсивностей отраженного и падающего потоков: Коэффициент прохождения – как отношения интенсивностей прошедшего и падающего потоков:

. Складывая выражения для R и Т, получаем . Данное равенство означает, что частица либо отражается от ступеньки, либо проходит во вторую часть. Если рассматривать не поток, а отдельно взятые частицы, то R – средняя вероятность отражения частиц от потенциальной ступеньки, а Т – средняя вероятность прохождения. Если частицы с движутся к ступеньке не ->, а <-, то также имеет место отражение. Причем R остается прежним, если и не менять. Для квантовых частиц любое резкое изменение всегда приводит к определенному отражению от этой области.

Туннельный эффект.

П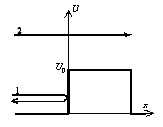 роанализируем теперь движение квантовой частицы. Пусть , тогда 1 – область слева от барьера, 2 - область барьера, 3 - область справа от барьера. Волновые функции частицы в этих областях обозначим соответственно. Запишем уравнение Шрёдингера для каждой области: Первая область

Вторая область: . Третья область: . Решения этих уравнений имеют вид (очевидно и ): , ,

Так как в первой области решение содержит отраженную волну, то это означает, что частица имеет конечную вероятность отражения от барьера (у классической частицы вероятность равна 1). Так как в третьей области есть прошедшая волна, то у частицы есть вероятность прохождения за барьер (с классической точки зрения в принципе не может быть). Такая способность квантовых частиц проникать сквозь потенциальный барьер при получила название туннельный эффект. Коэффициенты связаны между собой Эта связь может быть определена из условий непрерывности и на границах барьера: , , Для описания туннельного эффекта используются не сами коэффициенты, а их отношения. Вероятность отражения частицы от потенциального барьера – коэффициент отражения R и вероятность прохождения частицы сквозь барьер – коэффициент прозрачности барьера D. , . Оба коэффициента связаны соотношением.