3.3.1. Прямая задача

Дано: напряжения σ_х, σ_у, τ_ху, угол α > 0 (рис.3.8,а).

Определить: напряжения σ_α и τ_α (рис.3.8,б).

Рассмотрим равновесие элемента abc. При записи уравнений статики будем определять силу как произведение напряжения на площадь соответствующей грани:

площадь наклонной грани bc = dF;

площадь прямой грани ab = dF ∙ cos α;

площадь прямой грани ac = dF ∙ sin α..

а б в

Рис.3.8

Теперь запишем уравнения проекций всех сил, действующих на элемент abc, на нормаль к наклонной площадке и на ось, совпадающую с этой площадкой (рис.3.8,в).

∑n = 0: σ_αdF – σ_x dF cos α ∙ cos α – σ_у dF sin α ∙ sin α + τ_xу dF cos α ∙ sin α + τ_ух dF sin α ∙ cos α = 0,

∑t = 0: τ_αdF + σ_у dF sin α ∙ cos α + τ_уx dF sin α ∙ sin α – τ_xу dF cos α ∙ cos α – σ_х dF cos α ∙ sin α = 0.

После несложных преобразований и сокращения на dF получаем следующие выражения:

σ_α = σ_х cos²α + σ_y sin²α – τ_xy sin 2α , (3.9)

. (3.10)

Если исходные площадки являются главными (рис.3.9), то формулы (3.9) и (3.10) упрощаются: σα = σ1cos2α + σ2sin2, (3.11) . (3.12) Из формулы (3.12) следует, что наибольшее касательное напряжение действует по площадке, наклонённой под углом 450 к главным площадкам: . (3.13)

Рис.3.9

Преобразуем формулу (3.9), используя выражение для тригонометрических функций

и .

Получим

. (3.14)

Теперь определим напряжения, действующие по площадке, перпендикулярной к заданной: α₁ = α + 90⁰. Воспользуемся формулой (3.14), учитывая, что cos 2α₁ = – cos 2α и sin 2α₁ = – sin 2α. Получим

. (3.15)

Сложим (3.14) и (3.15), чтобы найти сумму нормальных напряжений, действующих по взаимно перпендикулярным площадкам.

Получим

σ_α + σ_{α + 90} = σ_х + σ_у = const, (3.16)

т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам инвариантна по отношению к наклону этих площадок.

3.3.2. Обратная задача

Дано: напряжения σ_х, σ_у, τ_ху (рис.3.8,а).

Определить: положение главных площадок и величины главных напряжений σ₁ и σ₂.

По определению на главных площадках τ_α = 0. Из формулы (3.10) найдём угол α₀ между осью х и одним из главных напряжений.

,

. (3.17)

Величины главных напряжений можно найти по формулам (3.14) и (3.15), подставив в них α₀. Удобнее иметь формулы для главных напряжений, не зависящие от углов и тригонометрических функций. Для вывода используем зависимости косинуса и синуса двойного угла от тангенса

, .

Подставим их в формулу (3.14):

. (*)

Теперь в выражение (*) подставим tg 2α₀ по формуле (3.17) и получим значение большего главного напряжения

.

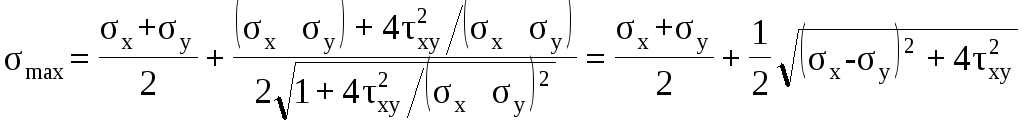Второе главное напряжение получим, используя формулу (3.15). В результате выражение для главных напряжений при плоском напряжённом состоянии имеет следующий вид:

. (3.18)

Для определения σ_max после первого слагаемого ставим «+», а для определения σ_min ставим «–». Следует обратить внимание на то, что если одно из главных напряжений, вычисленных по формуле (3.18), окажется отрицательным, то их следует обозначить σ₁ и σ₃. Если же оба главных напряжений окажутся отрицательными, то σ₂ и σ₃; оба положительными, то σ₁ и σ₂.

Главные напряжения обладают свойством экстремальности – одно из них наибольшее, другое – наименьшее из всех возможных в данной точке тела (помним о том, что сумма нормальных напряжений на взаимно перпендикулярных площадках постоянна). Для доказательства исследуем на экстремум функцию σ_α (формула 3.9). Продифференцируем её и приравняем производную нулю.



 – 2τ_xy cos 2α = (σ_x – σ_y)sin 2α  .

Площадки, характеризуемые этими углами, являются главными в соответствии с формулой (3.17).