
- •Корневые оценки качества
- •Степень устойчивости
- •Связь степени устойчивости с быстродействием
- •Степень колебательности
- •Понятие о расширенной афх
- •Частотные критерии качества
- •Интегральные оценки качества
- •Линейные интегральные оценки
- •Квадратичные интегральные оценки
- •Обобщённые квадратичные оценки
- •Контрольные вопросы
2. КОСВЕННЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА. КОРНЕВЫЕ ПОКАЗАТЕЛИ. СТЕПЕНЬ УСТОЙЧИВоСТИ. СТЕПЕНЬ КОЛЕБАТЕЛЬНОСТИ. ПОНЯТИЯ О РАСШИРЕННЫХ АФХ. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА - ПОКАЗАТЕЛЬ КОЛЕБАТЕЛЬНОСТИ. ИНТЕГРАЛЬНЫЕ КРИТЕРИИ КАЧЕСТВА
Построение графика переходного процесса требует достаточно громоздких вычислений. Поэтому для оценки качества переходного процесса чаще всего используют косвенные критерии, которые вычисляются относительно легко и которые связаны с определёнными характеристиками переходного процесса.
К ним относятся:
-
критерий распределения корней (корневые оценки);
-
частотные критерии;
-
интегральные критерии.
Корневые оценки качества
К корневым оценкам относятся степень устойчивости и степень колебательности.
Степень устойчивости
Степень устойчивости численно равна абсолютному значению действительной части ближайшего к мнимой оси корня (рис. 3).
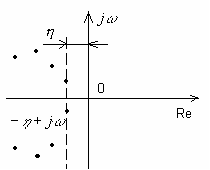
Рис. 3. К определению степени устойчивости
Система обладает достаточным запасом
устойчивости, если
![]() достаточно велико. Запишем уравнение
переходного процесса (движения
системы):
достаточно велико. Запишем уравнение
переходного процесса (движения
системы):
![]() .
(44)
.
(44)
Если
![]() ,
,
то
![]() ,
(45)
,
(45)
где
![]() .
.
Степень устойчивости характеризует интенсивность затухания переходного процесса (рис. 4).
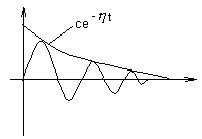
Рис. 4. Интерпретация степени устойчивости
Наименьшему по абсолютной величине корню соответствует наиболее медленно затухающая составляющая переходного процесса.
Связь степени устойчивости с быстродействием
Пусть за время tp
составляющая переходного процесса
![]() от значения h1(0)=C1
уменьшилась в m раз (рис.5).
от значения h1(0)=C1
уменьшилась в m раз (рис.5).
![]() ;
;
![]() ;
(46)
;
(46)
![]() ;
(47)
;
(47)
![]() ;
(48)
;
(48)
![]() .
(49)
.
(49)
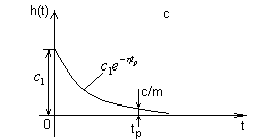
Рис. 5. К связи степени устойчивости с быстродействием
Увеличению времени tp
при m=const
соответствует уменьшение
![]() .
Чем больше
.
Чем больше
![]() ,
тем быстрее затухает процесс.
,
тем быстрее затухает процесс.
Степень колебательности
Из начала координат проведём лучи через два комплексно сопряжённых корня так, чтобы все остальные корни оказались между этими лучами (рис. 6).
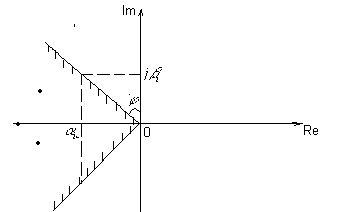
Рис. 6. К определению степени колебательности
Степенью колебательности называется отношение
![]() .
(50)
.
(50)
Из рис. 6 следует, что
![]() .
(51)
.
(51)
Чем больше m, тем быстрее затухает колебательный процесс. Степень колебательности характеризует запас устойчивости системы.
Если на систему накладывается требование
![]() ,
то это означает, что все корни
характеристического уравнения системы
должны находиться внутри заштрихованного
сектора.
,
то это означает, что все корни
характеристического уравнения системы
должны находиться внутри заштрихованного
сектора.
Для системы второго порядка с двумя комплексными сопряженными корнями уравнение движения
![]() .
(52)
.
(52)
Найдём связь степени колебательности и степени затухания. В выражение степени затухания (52) подставим:
![]() ,
(53)
,
(53)
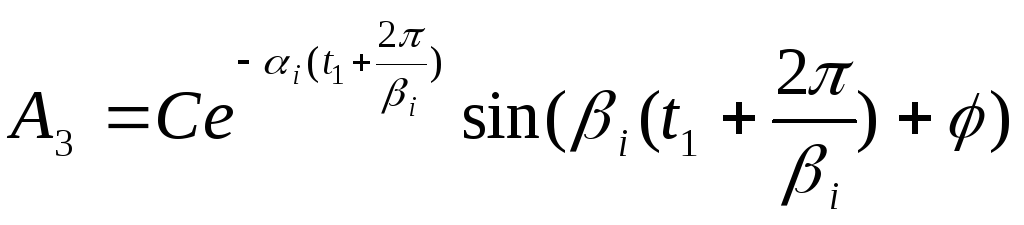 ,
(54)
,
(54)
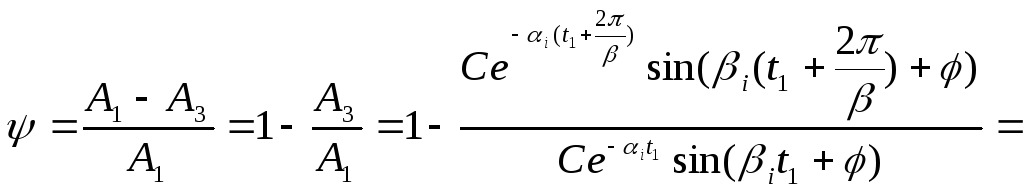
![]() .
(55)
.
(55)
Заметим, что для систем более высокого (>2) порядка соотношение (55) является приближённым. Степень его достоверности повышается в тех случаях, когда пара комплексных сопряжённых корней, определяющая m, имеет вещественную часть, значительно отличающуюся от вещественной части остальных корней.
При решении задач параметрического синтеза системы управления могут иметь место требования:
![]() (56)
(56)
или
![]() .
(57)
.
(57)
Для выполнения условий (56) и (57) можно воспользоваться расширенными АФХ разомкнутой системы.
Понятие о расширенной афх
Рассмотренные ранее [1] АФХ получали из
передаточной функции заменой
![]() .
.
![]() представляет собой отображение мнимой
оси
представляет собой отображение мнимой
оси
![]() комплексной плоскости корней
характеристического уравнения на
комплексную плоскость
комплексной плоскости корней
характеристического уравнения на
комплексную плоскость
![]() . (58)
. (58)
Отобразим на плоскости (58) луч, определяющий степень колебательности mз. Уравнение этого луча:
![]() ,
(59)
,
(59)
где ![]() - текущие значение
мнимой составляющей корня.
- текущие значение
мнимой составляющей корня.
АФХ, полученная отображением (59),
называется расширенной АФХ (РАФХ). Таким
образом, обычная АФХ представляет собой
отображение границы устойчивости
![]() ,
а РАФХ представляет собой отображение
линии, лежащей в левой полуплоскости
корней характеристического уравнения.
,
а РАФХ представляет собой отображение
линии, лежащей в левой полуплоскости
корней характеристического уравнения.
Для выбора параметров системы, обеспечивающих выполнение условий (56), (57), можно воспользоваться критерием устойчивости Найквиста [ 2].
Например, для выполнения условия
![]() параметры системы изменяют таким
образом, чтобы РАФХ при
параметры системы изменяют таким
образом, чтобы РАФХ при
![]() прошла через точку с координатами (-1,
j0).
прошла через точку с координатами (-1,
j0).
Для выполнения условия
![]() на плоскости АФХ отображается линия:
на плоскости АФХ отображается линия:
![]() (60)
(60)
комплексной плоскости корней
характеристического уравнения (рис. 3)
и подбираются параметры системы таким
образом, чтобы РАФХ разомкнутой системы
при (60) прошла через точку с координатами
![]() .
.
