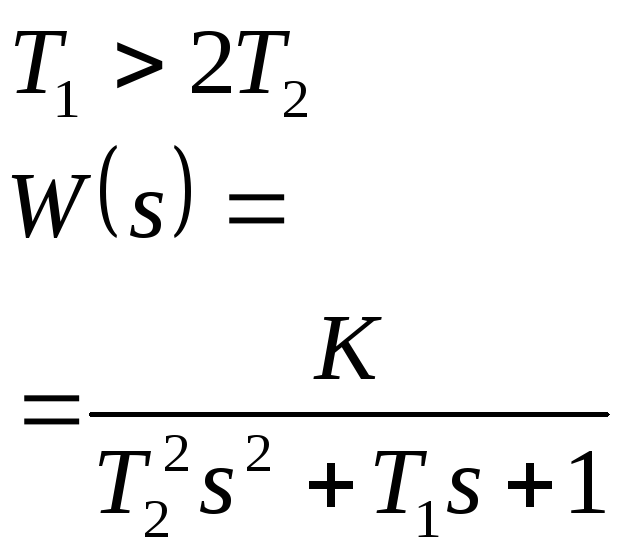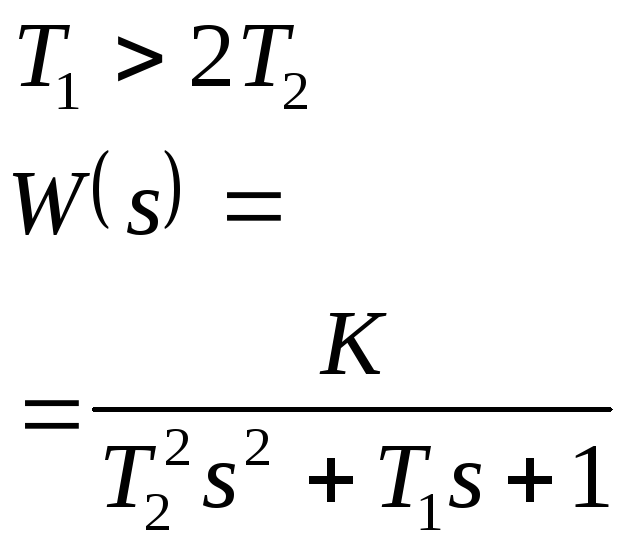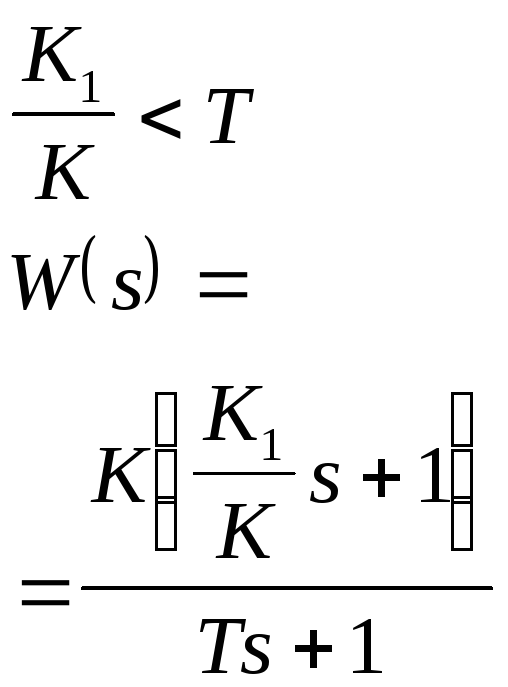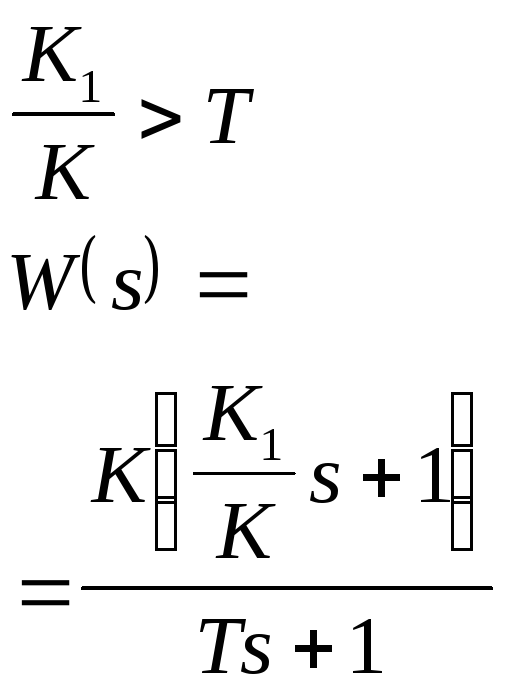6. Типовые динамические звенья. Принцип выделения звеньев. УсилитеЛьНое звено. Инерционные звенья 1-го и 2-го порядков

Несмотря на различное конструктивное оформление функциональных элементов в автоматических системах имеет место общность их математических выражений, связывающих входные и выходные величины. Можно выделить ограниченное число типовых алгоритмических звеньев.

Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.

Классификацию типовых звеньев удобно осуществлять, рассматривая различные частные формы дифференциального уравнения:

.(87)

В табл. 2 приведены значения коэффициентов уравнения (87), названия типовых звеньев, их передаточные функции.

Таблица 2

Типовые динамические звенья

№	Наименование звена						Примечание
1	2	3	4	5	6	7	8
1	Безынерционное пропорциональное	0	0	1	0	K
2	Инерционное первого порядка (апериодическое)	0	T	1	0	K
3	Инерционное второго порядка (апериодическое)			1	0	K

Таблица 2 (продолжение)

1	2	3	4	5	6	7	8
4	Инерционное второго порядка (колебательное)			1	0	K
5	Идеальное интегрирующее	0	1	0	0	K
6	Реальное интегрирующее	T	1	0	0	K
7	Идеальное дифференцирующее	0	0	1	K	0
8	Реальное дифференцирующее	0	T	1	K	0
9	Изодромное (пропорционально- интегрирующее)	0	1	0		K
10	Форсирующее (пропорционально- дифференцирующее)	0	0	1		K
11	Интегро- дифференцирующее с преобладанием интегрирующих свойств	0	T	1		K

Таблица 2 (окончание)

1	2	3	4	5	6	7	8
12	Интегродифферен­цирующее с преобладанием дифференцирующих свойств	0	T	1		K

Отметим общие закономерности звеньев. Если коэффициенты и, то звенья имеют однозначную связь между входной и выходной величиной в статическом режиме. Они называются статическими, или позиционными. Звенья, у которых,,илииилии, обладают инерционностью (замедлением). К ним относятся звенья 2, 3, 4, 6, 8, 11, 12.

У звеньев № 1, 5, 7 только два коэффициента не равны нулю. Они являются простейшими или элементарными. Все остальные могут быть образованы из элементарных путем последовательного, параллельного и встречно-параллельного соединения.

Рассмотрим свойства звеньев № 1-8. Характеристики остальных звеньев № 9, 12 могут быть получены как характеристики различных соединений звеньев № 1-8.

При рассмотрении указанных звеньев будут приведены следующие характеристики:

• уравнение звена и пример его физического представления;

• частотные характеристики;

• кривая разгона и импульсная переходная функция.

Временные характеристики есть реакция звена (элементов и т.д.) на апериодическое типовое воздействие. Реакция звена во времени на ступенчатое единичное воздействие 1(t) при нулевых начальных условиях называется переходной характеристикой (фун­кцией), или кривой разгона, и обозначается через h(t).

Реакция звена во времени на -функцию при нулевых начальных условиях называется импульсной переходной характеристикой (функцией). Она обозначается через.

Эти характеристики приведены на рис. 24 и 25.

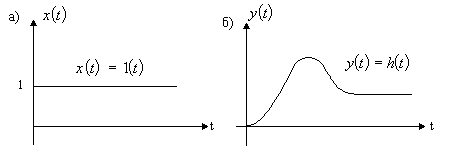
Рис. 24. Входное ступенчатое единичное воздействие (а) и кривая разгона (б)

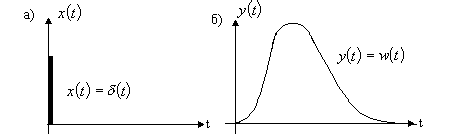
Рис. 25. Входное воздействие в виде -функции (а) и импульсная переходная функция

Переходные и импульсные переходные функции связаны между собой соотношениями:

, (88)

. (89)

При помощи импульсной функции звена можно определить его реакцию на произвольное входное воздействие.

Связь между входной и выходной величинами устанавливается интегралом Дюамеля (интегралом свертки):

или

. (90)

Переходная функция h(t) звена представляет собой решение неоднородного дифференциального уравнения звена при и придля i=1... n.

Она состоит из двух составляющих:

, (91)

где – возмущенная составляющая, определяемая частным решением неоднородного уравнения и равна;– свободная составляющая, определяемая частным решением соответствующего однородного дифференциального уравнения в виде:

, (92)

где – постоянные интегрирования, определяемые из начальных условий. Заметим, что собственный оператор D(p) представляет собой характеристическое уравнение, корни которогоестьв выражении (92).

В выражении передаточной функции звена знаменатель также представляет собой характеристическое уравнение, корни которого называются полюсами.

Корни числителя передаточной функции называются нулями. При значениях параметра P, равных нулям, передаточная функция W(P) обращается в ноль, а при значениях параметра P, равных полюсам, передаточная функция W(P) обращается в .