
- •4. Типы соединения звеньев. Передаточные функции эквивалентных звеньев. Правила структурных преобразований. Формула мейсона
- •Последовательное соединение
- •Параллельное соединение звеньев
- •Встречно-параллельное соединение (соединение с обратной связью)
- •Правила структурных преобразований
- •Формула Мейсона
- •Контрольные вопросы
- •5. Частотные характеристики. Амплитудно-фазовая характеристика. Связь амплитудно-фазоВой характеристиКи с передаточной функцией. Логарифмические частотные характеристики
- •Логарифмические частотные характеристики
- •Контрольные вопросы
4. Типы соединения звеньев. Передаточные функции эквивалентных звеньев. Правила структурных преобразований. Формула мейсона
При наличии большого числа элементов в системе пользуются структурным методом, согласно которому уравнение всей системы получают на основе алгоритмической схемы при помощи нескольких простых правил.
Сущность метода состоит в том, что по известным передаточным функциям отдельных элементов системы, представляющих собой детектирующие звенья однонаправленного действия, используя правила последовательного, параллельного и встречно-параллельного (с обратной связью) соединений звеньев, получают эквивалентную передаточную функцию, или передаточную функцию эквивалентного звена. В результате получают одноконтурную замкнутую цепочку, состоящую из нескольких эквивалентных звеньев. Причем эта цепочка может иметь несколько входов и несколько выходов. Далее согласно одноконтурной схеме записывают передаточные функции между разомкнутыми входами и выходами системы. Рассмотрим типы соединения звеньев.
Последовательное соединение
Здесь выход предыдущего звена является входом в последующее. Пусть имеется N последовательно соединенных звеньев (рис. 12).
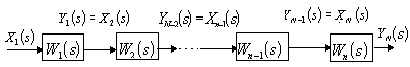
Рис. 12. Последовательное соединение звеньев
Начнем рассмотрение с последнего звена:
![]() ,(43)
,(43)
далее
![]() .(44)
.(44)
Из (44) найдем
![]() :
:
![]() .(45)
.(45)
Подставляя (45) в (43), получим для двух последних звеньев:
![]() .(46)
.(46)
Распространяя этот подход до первого звена включительно, окончательно получим:
![]() .(47)
.(47)
Передаточная функция эквивалентного звена, представляющего N последовательно соединенных звеньев, равна произведению передаточных функций этих звеньев.
Параллельное соединение звеньев
Параллельным соединением звеньев называется такое соединение, при котором на выход всех элементов поступает одно и то же воздействие, а их выходные величины алгебраически суммируются (рис. 13):
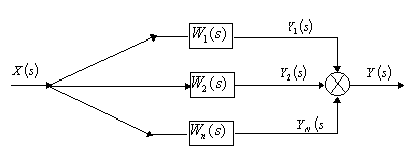
Рис. 13. Параллельное соединение звеньев
Введем обозначения:
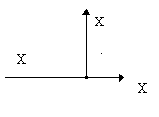 –
узел разветвления сигнала,
–
узел разветвления сигнала,
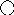
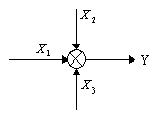 – узел суммирования сигналов.
– узел суммирования сигналов.
Запишем уравнение движения в преобразованном по Лапласу виде:
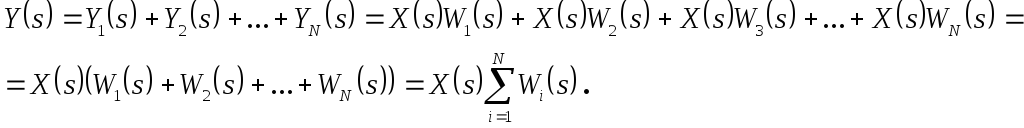
Или
![]() .(48)
.(48)
Передаточная функция эквивалентного звена, представляющего N параллельно соединенных звеньев, равна сумме передаточных функций этих звеньев.
Встречно-параллельное соединение (соединение с обратной связью)
Встречно-параллельным соединением двух элементов называют такое соединение, при котором выходной сигнал второго элемента поступает на выход второго, а выходной сигнал второго элемента алгебраически суммируется с общим входным сигналом. Схема встречно-параллельного соединения показана на рис. 14:

Рис. 14. Встречно-параллельное соединение (соединение с обратной связью)
Запишем уравнение движения:
![]() ,(49)
,(49)
![]() ,(50)
,(50)
![]() .(51)
.(51)
Подставляя (51) и (50) в (49), получим:
![]() .(52)
.(52)
Приведя подобные члены, получим:
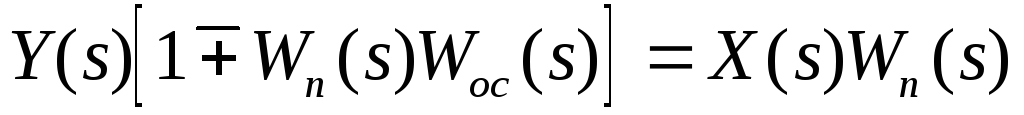 .(53)
.(53)
Из (53)
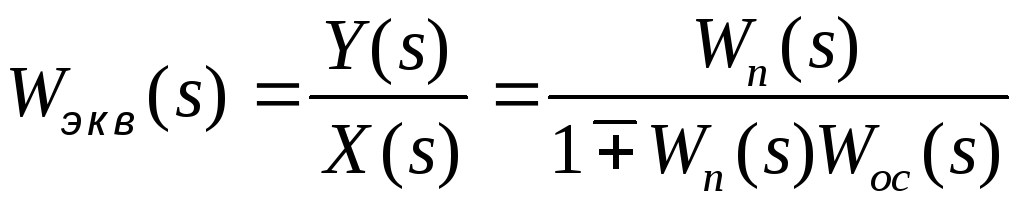 . (54)
. (54)
Знак (-) для положительной обратной связи, когда
![]() .
.
Знак (+) для отрицательной обратной связи, когда
![]() .
.
Элемент, в котором направление передачи сигнала совпадает с направлением передачи общего сигнала, называют элементом прямой цепи.
Элемент, в котором направление передачи сигнала противоположно направлению передачи общего сигнала, называют элементом обратной связи.
Передаточная функция эквивалентного звена при встречно-параллельном соединении звеньев равна отношению передаточной функции звена прямой цепи к знаменателю, представляющему собой алгебраическую сумму единицы и произведения передаточных функций звена прямой цепи и звена обратной связи.
Если автоматическая система имеет так называемые перекрестные обратные связи, то кроме замены звеньев эквивалентными звеньями приходится использовать дополнительные правила структурных преобразований.
Передаточная функция замкнутой системы, представленная в виде эквивалентной одноконтурной схемы, имеет вид:
![]() , (55)
, (55)
где ![]() –
эквивалентная передаточная функция
звеньев, находящихся в прямой цепи между
рассматриваемым входом и выходом;
–
эквивалентная передаточная функция
звеньев, находящихся в прямой цепи между
рассматриваемым входом и выходом;
![]() –
эквивалентная передаточная функция
звеньев, образующих обратную (по отношению
к рассматриваемой прямой цепи) связь.
–
эквивалентная передаточная функция
звеньев, образующих обратную (по отношению
к рассматриваемой прямой цепи) связь.
Главная обратная связь в любой автоматической системе управления всегда отрицательна. Поэтому в знаменателе (55) взят знак «+». В знаменателе передаточной функции (55) записано произведение эквивалентных передаточных функций, представляющее собой произведение передаточных функций всех звеньев, последовательно соединенных друг с другом в главном контуре системы, то есть
![]() . (56)
. (56)
Передаточная функция (56) называется
передаточной функцией разомкнутой
системы и обозначается
![]() или
или![]() .
.
В общем случае к системе может быть приложено несколько воздействий (рис. 15):
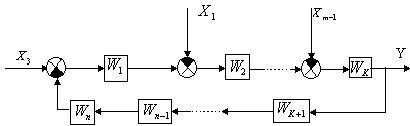
Рис. 15. Система управления с несколькими внешними воздействиями
Однако по каждому каналу передачи
воздействия на выходную величину Y в
передаточной функции замкнутой системы
знаменатель будет определен одним и
тем же соотношением вида
![]() ,
а в числителе передаточная функция
,
а в числителе передаточная функция![]() будет
определяться произведением передаточных
функций звеньев, заключенных между
узлом суммирования в точке приложения
воздействия и узлом разветвления для
выходной величины.
будет
определяться произведением передаточных
функций звеньев, заключенных между
узлом суммирования в точке приложения
воздействия и узлом разветвления для
выходной величины.
В этом случае для линейных систем, подчиняющихся принципу суперпозиции, выходная величина равна:
![]() .(57)
.(57)
Перепишем соотношение (57) в виде:
![]() .(58)
.(58)
Выражение
![]() есть собственный оператор системы. Если
приравнять его к нулю, то получим
характеристическое уравнение одноконтурной
системы:
есть собственный оператор системы. Если
приравнять его к нулю, то получим
характеристическое уравнение одноконтурной
системы:
![]() .(59)
.(59)
При более сложном соединении звеньев для получения передаточной функции системы по выбранному каналу пользуются правилами структурных преобразований, приведенных в табл. 1.
Таблица 1
