
Dolhikh_1
.pdf
|
|
|
|
|
|
|
Скалярний добуток в ортонормованому базисі |
|
|||||||||||||||||||||||||||||||
|
|
У базисі i , j, k |
|
|
|
скалярний добуток векторів |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
aG = axiG + ay Gj + az kG |
= (ax ,ay ,az ), |
b =bxi + by j + bz k = (bx ,by ,bz ) |
|||||||||||||||||||||||||||||||||||
дорівнює сумі добутків їх відповідних координат: |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
G |
= axbx + ayby |
+ azbz . |
|
|
|
|
|
(3.18) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
||||||||||||||||||||
|
|
Z Виразимо скалярний добуток через координати векторів aG і b , |
|||||||||||||||||||||||||||||||||||||
використовуючи алгебраїчні властивості 1-4: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
aG bG |
=(axiG |
+ ay Gj + azkG) (bxiG+by j +bzk ) = axbxi i +axbyi j +axbziG kG+ |
||||||||||||||||||||||||||||||||||||
|
|
+ a ybx Gj iG + a yby Gj Gj + aybz j k + azbx k i + azby k j + azbz kG kG = |
|||||||||||||||||||||||||||||||||||||
={i i = j j = k k =1 1 cos0D |
=1, |
|
i j = i k = j k =1 1 cos90D = 0} = |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= axbx + ayby + azbz . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
Деякі важливі формули |
|
|
|
|
||||||||||||||
• |
|
довжина вектора |
|
|
|
a |
= (ax ,ay ,az ) : |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aG |
|
= |
ax2 + a 2y |
+ az2 ; |
|
|
|
|
|
|
(3.19) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
• відстань між двома точками А(х1, у1, z1) і В(х2, у2, z2): |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
AB |
|
= |
|
|
(x |
2 |
|
− x )2 + ( y |
2 |
− y )2 |
+ (z |
2 |
− z )2 |
; |
|
|
(3.20) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|||
• |
|
косинус кута між векторами a і b : |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
axbx + ayby + azbz |
|
|
|
|
|||||||||
|
|
|
|
|
|
cosϕ = |
|
|
a |
|
|
b |
= |
|
|
|
|
|
; |
|
|
(3.21) |
|||||||||||||||||
|
|
|
|
|
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
ax2 + a2y + az2 bx2 +by2 +bz2 |
|
|
|
|
|||||||||||||||
• необхідна й достатня умова перпендикулярності двох векторів: |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
G |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
b ; |
|
|
|
(3.22) |
|||
|
|
|
|
|
|
|
|
a |
b |
= axbx +ayby +azbz = 0 a |
|
|
|
||||||||||||||||||||||||||
• |
|
проекція |
вектора |
|
|
b |
на |
вектор |
a |
|
b |
|
|
|
|
||||||||||||||||||||||||
|
|
(рис. 3.15): |
|
G |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
G |
|
G |
|
|
|
|
|
|
a b |
|
|
G |
G |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ПрaGb |
= |
b |
|
cosϕ = |
|
|
aG |
|
|
|
|
=b a0 = |
|
|
|
(3.23) |
|
ϕ |
|
|
|
aG |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aG |
|
|
|
|
|
|
|
||||||||
|
|
axbx + ayby + azbz |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
a0 |
= |
|
|
G |
|
. |
|
|
|
|
|
|
ПрaGb = |
b |
cosϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ax2 + a2y + az2 |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.15 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ДВНЗ “Українська академія банківської справи НБУ” |
|
|
|
51 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
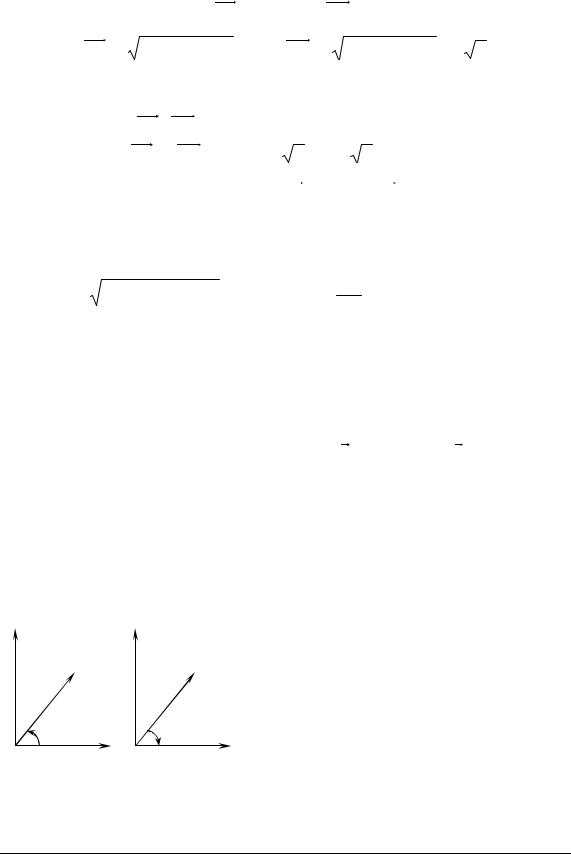
Приклад 3.4. Дано вершини трикутника А(−1, −2, 4); В(−4, −2, 0); С(3, −2, 1). Визначити його внутрішній кут ϕ при вершині B.
► Знайдемо вектори BA= (3, 0, 4), BC = (7, 0, 1) та їх довжини:
|
|
|
BA |
= 32 + 02 + 42 =5, |
BC |
= 72 + 02 +12 =5 2. |
|||||||||||||||||
|
За формулою (3.21) обчислимо косинус кута ϕ між векторами |
||||||||||||||||||||||
|
|
cosϕ = |
BA BC |
= |
3 7 + 0 + 4 1 |
= |
|
1 |
|
|
ϕ = 45D. |
||||||||||||
|
|
|
5 5 2 |
|
|
2 |
|
||||||||||||||||
|
|
|
|
| BA | | BC | |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Приклад 3.5. Дано три вектори a =(1, −3, 4), b =(3, −4, 2), cG=(−1,1, 4). |
||||||||||||||||||||||
Знайти ПрbG+cGaG. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
► Введемо вектор d =b + cG = (2, −3, 6) |
та обчислимо його дов- |
|||||||||||||||||||||
|
|
G |
|
|
|
|
|
G |
d |
|
|
|
2 |
|
3 |
|
6 |
|
|||||
жину | d |= 22 + (−3) |
2 + 6 |
2 |
= 7 і орт d0 = |
G |
|
= |
7 |
, − |
7 |
, |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| d |
|
| |
|
|
|
7 |
|
|||
G |
За формулою (3.23) знайдемо проекцію |
вектора aG на вектор |
|||||||||||||||||||||
G |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d |
=b |
+ c : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
G |
G |
G |
|
2 |
|
|
|
|
|
3 |
|
|
|
6 |
|
35 |
=5. |
|
|
|
ПрbG+cGa = ПрdGa |
= a d0 =1 |
7 |
+ (−3) − |
7 |
+ 4 |
7 |
= |
7 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Приклад 3.6. При якому m вектори |
a = (m, −3, 4), |
b = (4, − 4, 2m) |
||||||||||||||||||||
взаємно перпендикулярні?
рів: aG►bGНеобхідна= 0 . й достатня умова перпендикулярності двох векто- aG bG = axbx + ayby + azbz = 4m +12 +8m =12m +12 = 0 m = −1.
3.11. ВЕКТОРНИЙ ДОБУТОК ВЕКТОРІВ
cG |
b |
cG |
|
|
|
a |
|
|
|
|
|
ϕ |
a |
ϕ |
b |
Права трійка |
Ліва трійка |
||
Рис. 3.16. Права і ліва трійки
Впорядкована трійкаG некомпланарних векторів aG, b, cG називається
правою (лівою), якщо після зведення до спільного початку найкоротший
поворот від вектора aG до вектора b , що спостерігається з кінця вектора c , здійснюється проти обертання стрілки годинника (за стрілкою годинника) (рис. 3.16).
ДВНЗ “Українська академія банківської справи НБУ”
52

Декартова система координат, що пов’язана з трійкою i , j, k , є
правою. Векторним добутком векторівG aG і
b називається вектор cG = aG×b , що задовольняє таким умовам (рис. 3.17):
1)довжина вектора c дорівнює добутку
довжин векторів a і b на синус кута між ними, тобто | cG|=| aG|| b | sin ϕ ;
2)вектор c перпендикулярний кожномуG із векторів , тобто cG aG, cG b ;і ba
|
Рис. 3.17. Векторний |
3) |
вектор c |
напрямлений так, що векто- |
|||
добуток векторів aG і b |
|
ри a , b , c |
утворюють праву трійку |
||||
|
G |
G |
Алгебраїчні властивості векторного добутку |
||||
1) |
G |
G |
|
(антикомутативна властивість); |
|||
a |
×b |
= −b |
×a |
|
|||
2) |
λ(aG×b) = (λaG) ×b = aG×(λb) |
(асоціативна властивість); |
|||||
3) |
aG×(b + cG) = aG×b + aG×cG |
|
(дистрибутивна властивість); |
||||
4) |
aG×aG = 0 . |
|
|
|
|
||
Геометричні властивості векторного добутку
1.Необхідною й достатньою умовою колінеарності двох ненульових векторів є рівність нулюG×bGїхнього= 0 векторного добутку:|| b .a (3.24)a
2.Модуль векторного добутку векторів a і b дорівнює площі пара-
лелограма, побудованогоS = aG×наbцих. векторах (див. рис. 3.17): (3.25)
3.Площа трикутника, побудованого на векторах a і b :
|
|
|
|
|
1 |
|
G |
G |
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
S = 2 |
|
a |
×b |
|
. |
(3.26) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Векторний добуток в ортонормованому базисі |
|||||||||
|
|
В базисі i , j, k векторний добуток векторів |
|||||||||||
|
aG = axiG |
+ ay |
Gj + az kG = (ax ,ay ,az ), |
b =bxi + by j + bz k = (bx ,by ,bz ), |
|||||||||
обчислюється за формулою: |
|
|
|
|
|||||||||
aG |
×bG |
|
iG |
Gj |
k |
|
= (aybz − azby )iG + (azbx − axbz )Gj + (axby − aybx )kG. (3.27) |
||||||
|
|
||||||||||||
= |
ax |
ay |
az |
|
|||||||||
|
|
|
bx |
by |
bz |
|
|
|
|
|
|
||
ДВНЗ “Українська академія банківської справи НБУ”
53

Z Використаємо алгебраїчні властивості 1-4:
aG×b =(axi +ay j +azk) ×(bxi +by j +bzk) =axbxi ×i +axbyi × j +axbzi ×k + +aybx Gj ×iG+ayby Gj × Gj +aybz Gj ×kG+azbxkG×iG+azbykK× Gj +azbzkG×kG=
={i ×i = j × j = k ×k = 0, i × j = k = − j ×i , i ×k = − j = k ×i ,
Gj ×kG = iG = −k × Gj} = (aybz − azby )i + (azbx − axbz )j + (axby − aybx )k.
Наслідок. Вектори a = (ax ,ay ,az ) і b = (bx ,by ,bz ) колінеарні тоді і тільки тоді, коли їх координати пропорційні, тобто:
a x |
= |
a y |
= |
a z |
aG|| b. |
(3.28) |
bx |
|
b y |
|
bz |
|
|
Приклад 3.7. Знайти площу трикутника з вершинами A(1, −1, 2), B(5, −6, 2), C(1, 3, −1) та довжину висоти h, опущеної з вершини В на сторону АС.
► Площа трикутника дорівнює половині модуля векторного до-
бутку векторів AB = (4, −5, |
0) i |
AC = (0, 4, −3). |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
k |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Оскільки AB × AC = |
4 |
|
|
−5 |
0 |
=15i +12 j +16k, то |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
4 |
−3 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
152 |
+122 +162 = |
625 |
|
|
25 |
|
(од.2). |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
S = |
|
|
AB × AC |
= |
|
|
|
|
|
|
|
|
|
= |
|
|
||||||||||
2 |
2 |
|
2 |
|
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
З іншого боку, площу трикутника можна обчислити за формулою |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
S = |
AC |
h / 2, звідки знаходимо висоту трикутника: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
h = |
|
|
2S |
|
|
|
= |
|
|
25 |
=5. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
AC |
|
|
|
02 + 42 + (−3)2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.12. МІШАНИЙ ДОБУТОК ВЕКТОРІВ
Мішаним добутком трьох векторів називається число, яке дорівнює векторному добутку aG×b , помноженому скалярно на вектор cG: (aG×b) cG.
Основна алгебраїчна властивість мішаного добутку
Циклічна перестановка трьох множників мішаного добутку не змінює його значення; перестановка двох сусідніх множників змінює
знак добутку:
(aG×bG) cG=(bG×cG) aG=(cG×aG) b =−(b ×aG) cG=−(cG×b) aG=−(aG×cG) bG. (3.29)
ДВНЗ “Українська академія банківської справи НБУ”
54
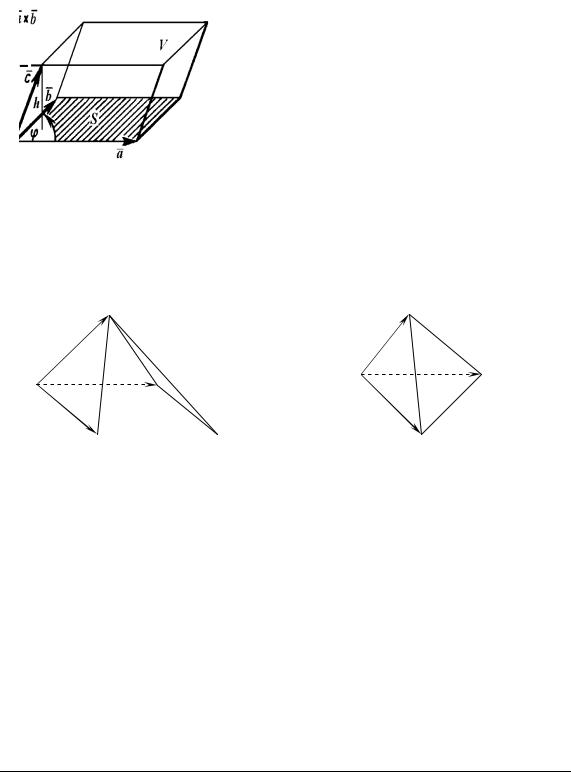
Геометричні властивості мішаного добутку
1.Мішаний добуток некомпланарних векторів aG, b, cG дорівнює
об’єму паралелепіпеда, побудованого на цих векторах, взятому зі
знаком плюс, якщо трійка векторів aG, b, cG права, і зі знаком мінус, якщо трійка aG, b, cG ліва.
|
|
|
|
|
|
|
|
|
Z Нехай e – орт векторного до- |
|||||||||
|
|
|
|
|
|
|
|
|
бутку векторів aG×b , тоді |
|
||||||||
|
|
|
|
|
|
|
|
|
aG×b = S eG (aG×b) cG = S eG cG = |
|||||||||
|
|
|
|
|
|
|
|
|
= S ПрeGcG = ±S h = ±V. |
|
||||||||
|
|
|
|
|
|
|
|
|
Об’єм паралелепіпеда, побудова- |
|||||||||
|
|
Рис. 3.18 |
|
|
ного на векторах aG, b, cG (рис. 3.18): |
|||||||||||||
|
|
|
|
V = |
|
(aG×b ) cG |
|
. |
|
|
(3.30) |
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||||
2. Об’єм |
чотирикутної |
пірамі- |
3. Об’єм трикутної піраміди: |
|
||||||||||||||
ди: |
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
V = |
1 |
|
(aG×bG) cG |
|
. |
(3.31) |
V = 16 |
|
(aG×b ) cG |
|
. |
(3.32) |
||||||
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||
cG |
3 |
|
|
|
|
|
|
|
c |
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bG |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||
aG |
|
|
|
|
|
|
|
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Рис. 3.19. |
|
|
|
|
Рис. 3.20. |
|
||||||||||
Чотирикутна піраміда |
Трикутна піраміда |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Необхідною й достатньою умовою компланарності трьох векторів є рівність нулю їх мішаного добутку:
(aG×bG) cG = 0 вектори aG, b, cG компланарні. |
(3.33) |
5. Якщо (aG×bG) cG > 0 − трійка векторів aG, b, cG права; |
(3.34) |
(aG×bG) cG < 0 − трійка векторів aG, b, cG ліва. |
|
Мішаний добуток в ортонормованому базисі |
|
У базисі i , j, k мішаний добуток векторів |
a =(ax,ay,az ), |
bG=(bx ,by ,bz ), cG =(cx ,cy ,cz ) дорівнює визначнику, що складається з координат цих векторів:
ДВНЗ “Українська академія банківської справи НБУ”
55

(aG×bG) cG |
|
a |
a |
a |
|
|
= |
bx |
by |
bz |
. |
(3.35) |
|
|
|
x |
y |
z |
|
|
|
|
cx |
cy |
cz |
|
|
Необхідна й достатня умова компланарності трьох векторів:
|
|
|
|
|
|
|
(aG×bG) cG |
|
|
ax |
ay |
|
|
az |
|
|
|
|||
|
|
|
|
|
|
|
= |
|
bx |
by |
|
|
bz |
|
= 0. |
(3.36) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cx |
cy |
|
|
cz |
|
|
|
G |
Приклад 3.8. |
Чи |
є |
компланарними |
вектори |
a = (2, −1, 3) , |
||||||||||||||
b |
= (−2, 3, 2) , с = (0, 2, 5) ? |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
► Три вектори компланарні, якщо їх мішаний добуток дорівнює |
|||||||||||||||||||
нулю: |
−1 |
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|||
(aG |
×bG) cG= |
|
2 |
3 |
|
={e |
|
+ e } = |
|
2 |
3 |
|
= 0 − вектори компланарні. |
|||||||
|
|
|
|
|
||||||||||||||||
|
− 2 |
3 |
2 |
|
2 |
|
0 |
2 |
5 |
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
5 |
|
|
|
|
|
|
|
0 |
2 |
5 |
|
|
|
|
|
Приклад 3.9. З’ясувати, яку трійку (праву чи ліву) утворюють век-
тори aG= (1, 1, 2), b = (−1, 3, 2), с= (2, 8, 1) і знайти об’єм трикутної піраміди, побудованої на цих векторах.
► За формулою (3.35) обчислимо мішаний добуток векторів:
G |
G |
G |
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
−1 3 |
2 |
|
|
+ e1 |
|
= |
||||
(a |
×b ) c |
|
|
= e2 |
|
|||||||
|
|
|
|
|
2 |
8 |
1 |
|
|
|
|
|
|
|
|
|
|
|
e3 |
− 2e1 |
|
||||
1 |
1 |
2 |
|
4 |
4 |
|
|
|
|||||
0 |
4 |
4 |
= |
= −36. |
||
0 |
6 |
−3 |
|
6 |
−3 |
|
|
|
|
|
Оскількимішанийдобутоквід’ємний− трійкавекторів aG, b, с ліва. Об’єм трикутної піраміди обчислюємо за формулою (3.32):
V= 16 (aG×bG) cG = 16 | −36 |= 6 (од.3).
3.13.ВЕКТОРИ В n-ВИМІРНОМУ ПРОСТОРІ
3.13.1.Поняття про n-вимірний векторний простір
Множина впорядкованих сукупностей п чисел (х1, х2,…, хп) нази-
вається п-вимірним координатним простором Ап.
Кожну сукупність (х1, х2,…, хп) називають точкою цього простору і позначають M(х1, х2,…, хп).
Точка О(0, 0, ..., 0) називається початком координат в Ап.
ДВНЗ “Українська академія банківської справи НБУ”
56

Вектор OM = (x1, x2 ,..., xn ) називається радіусом-вектором точки M. Його компоненти збігаються з координатами точки M. Таким чином, n-вимірний вектор − впорядкована сукупність п чисел (компонент вектора).
Зауваження. Компоненти вектора можуть мати неоднакові одиниці виміру. Це дозволяє поєднати в одній векторній величині декілька скалярних величин і далі оперувати з цим набором як з векторною величиною. Наприклад, норми витрат ресурсів на випуск одиниці продукції характеризуються кількістю одиниць відповідного ресурсу (сировини різних видів, устаткування, робочої сили, палива і т.д.), які виражаютьсяGв різних одиницях.
Вектор 0 G= (0, 0, ..., 0) називається нульовим.
Вектори x = (x1, x2 ,..., xn ) і y = ( y1, y2 ,..., yn ) вважаються рівними, якщо рівні їх відповідні компоненти, тобто x = y xi = yi (i =1, n).
Лінійні операції над векторами
Добутком вектора xG = (x1, x2 ,..., xn ) на число λ називається вектор
|
|
|
|
λx = (λx1, λx2 ,...,λxn ). |
(3.37) |
Сумою векторів |
xG = (x1, x2 ,..., xn ) і y = ( y1, y2 ,..., yn ) |
називається |
|||
вектор |
|
|
x + y = (x1 + y1, x2 + y2 ,..., xn + yn ). |
(3.38) |
|
|
|
|
|||
Різницею векторів xG = (x1, x2 ,..., xn ) і y = ( y1, y2 ,..., yn ) |
називається |
||||
вектор |
G |
G |
G |
G |
(3.39) |
|
x |
− y |
= x +(−1) y = (x1 − y1, x2 − y2 ,..., xn − yn ). |
||
Множина всіх п-вимірних векторів, для яких введені операції додавання й множення на дійсне число, називається п-вимірним лінійним векторним простором і позначається Rп.
3.13.2. Лінійна незалежність векторів. Базис і координати
Означення лінійно незалежної системи векторів дано у розді-
лі 3.3. Доведемо лінійну незалежність системи векторів: |
|
eG1 = (1, 0,..., 0), eG2 = (0, 1,..., 0), ..., en = (0, 0,...,1). |
(3.40) |
Z Для цього покажемо, що їх лінійна комбінація дорівнює нулю тільки при нульових коефіцієнтах, тобто:
c1eG1 +c2eG2 +... +cneGn = 0 c1 = c2 =…= cn = 0. c1(1, 0,…, 0)+c2(0, 1,…, 0)+…+cn(0, 0,…,1) = (0, 0,…, 0)
ДВНЗ “Українська академія банківської справи НБУ”
57

(c1, 0,…, 0)+(0, c2,…, 0)+…+(0, 0,…, cn) = (0, 0,…, 0)(c1, c2,…, cn) = (0, 0,…, 0) c1 = c2…= cn = 0.
Таким чином, система векторів (3.40) лінійно незалежна. Максимальна кількість лінійно незалежних векторів простору нази-
вається розмірністю простору. Покажемо, що Rn – n-вимірний простір.
Z Вектори e1, e2 , ..., en лінійно незалежні, а система векторів e1, eG2 , ..., eGn , xG = (х1, x2,…, xn) уже лінійно залежна, оскільки вектор x
можнаG представитиG уGвигляді лінійної комбінації інших векторів: x = = x1 e1 + x2 e2 +…+ xn en . Таким чином, розмірність простору Rn дорів-
нює n.
Базисом n-вимірного простору називається будь-яка впорядкована сукупність n лінійно незалежних (базисних) векторів. Одним із базисів простору Rn є сукупність векторів (3.40). Крім цього базису, в
n-вимірному просторі існує незліченна безліч інших базисів. |
|
|||
|
Будь-який вектор x n-вимірного простору може бути розкладе- |
|||
ний по лінійно незалежних векторах q1 , q2 ,…, qn : |
|
|||
|
xG = λ1 q1 + λ2 q2 +…+ λn qn . |
(3.41) |
||
|
Числа λ1, λ2,…, λn називаються координатами вектора xG |
у дано- |
||
му базисі. |
Gвектора |
|
|
|
|
Зауваження. Для |
x = (х1, x2,…, xn) числа х1, x2,…, xn є |
||
координатами у базисі |
e1, e2 , ..., en . |
|
||
|
3.13.3. Евклідів n-вимірний простір En |
|
||
|
Нехай у базисі e1 = (1, 0,…, 0), e2 = (0, 1,…, 0),…, en = (0, 0,…, 1) |
|||
простору Rn задані вектори x = (x1, x2,…, xn) і y = ( y1, y2 ,..., yn ) . |
||||
|
Скалярним добутком векторів x і y називається число |
|
||
|
(xG, yG) = x1y1 + x2y2 +…+ xnyn. |
(3.42) |
||
|
Алгебраїчні властивості скалярного добутку |
|
||
1) |
(xG, yG) = ( yG, x) |
|
(комутативна властивість); |
|
2) |
(xG+ yG, zG) = (xG, zG) +( yG, z) |
(дистрибутивна властивість); |
|
|
3) |
(λxG, yG) = (x, λyG) = λ(xG, y) |
(асоціативна властивість); |
|
|
4) |
(xG, xG) ≥ 0, причому (x, x) = 0 лише при xG = 0 . |
|
||
Лінійний векторний простір Rn, в якому визначений скалярний
добуток із властивостями 1-4, називають n-вимірним евклідовим прос-
тором Еn.
Нормою (довжиною) вектора x називається величина
xG |
|
|
|
= |
(xG, xG)= x2 |
+ x2 |
+... + x2 . |
(3.43) |
|
|
|||||||
|
|
|
|
|
1 |
2 |
n |
|
ДВНЗ “Українська академія банківської справи НБУ”
58
Вектор xG називається нормованим, якщо |
|
|
|
x |
|
|
|
|
=1. |
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
Будь-який вектор xG |
|
|
|
|
|
|
|
|
|
|||||||||||||
можна нормувати. Для цього необхідно поді- |
||||||||||||||||||||||
лити вектор (кожну координату вектора) на його норму. |
|
|||||||||||||||||||||
Відстань між двома точками А(a1, a2, …, an) і В(b1, b2, …, bn) об- |
||||||||||||||||||||||
числюється за формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
AB |
|
|
|
= (b − a )2 |
+ (b |
− a |
2 |
)2 +... + (b |
− a |
n |
)2 . |
(3.44) |
|||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
n |
|
|
|
||||
Нерівність Коші-Буняковського
Теорема. Для довільних векторів x і y виконується нерівність:
(x, y) |
|
≤ |
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
(3.45) |
|
|
|
|
|
|
|
|
|
Z За властивістю 4 скалярного добутку, для будь-якого λ виконується нерівність:
(x +λy, x +λy)≥ 0 (x, x) +(λy, x) +(x, λy) +(λy, λy) ≥ 0

 xG
xG
 2 +2λ(xG, yG) +λ2
2 +2λ(xG, yG) +λ2 
 yG
yG
 2 ≥ 0 .
2 ≥ 0 .
Квадратний тричлен відносно λ невід’ємний, отже, його графік
лежить вище осі λ, а це може бути лише у випадку, коли його дискримінант менше нуля, тобто (xG, yG)2 −
 xG
xG
 2
2 
 yG
yG
 2 ≤ 0 , звідси (x, y) ≤
2 ≤ 0 , звідси (x, y) ≤ 
 xG
xG


 yG
yG
 .
.
Нерівність трикутника (нерівність Мінковського)
Теорема. Длядовільнихвекторів x і y виконуєтьсянерівність:
xG + yG |
|
|
|
≤ |
|
|
|
xG |
|
|
|
+ |
|
|
|
yG |
|
|
|
(3.46) |
|
|
|
|
|
|
|
|
|
|
Z Обчислимо квадрат норми суми векторів з урахуванням нерівності Коші-Буняковського (3.45):

 xG + yG
xG + yG
 2 = (xG + yG, xG + yG) = (xG, xG) + 2(xG, yG) + ( yG, yG) ≤
2 = (xG + yG, xG + yG) = (xG, xG) + 2(xG, yG) + ( yG, yG) ≤
≤ 
 xG
xG
 2 + 2
2 + 2
 xG
xG


 y
y
 +
+ 
 y
y
 2 = (
2 = (
 xG
xG
 +
+ 
 y
y
 )2
)2 
 xG + yG
xG + yG
 ≤
≤ 
 xG
xG
 +
+ 
 y
y
 .
.
Кут між векторами в евклідовому просторі En
Косинус кута φ між векторами x і y визначається за формулою:
cosϕ = |
|
(Gx |
, |
yG) |
|
, 0 ≤ϕ ≤π. |
(3.47) |
|
|
|
|||||
|
|
x |
y |
|
|
|
Формула (3.47) є коректною, тому що за нерівністю КошіБуняковськогоправачастиназаабсолютноювеличиноюнеперевищує 1.
ДВНЗ “Українська академія банківської справи НБУ”
59

|
Якщо (x, yG) |
= 0, то φ=π/2 і вектори x , y |
називають ортогона- |
|||||||||||||||||||||||||||||||||||||||||||||||
льними (перпендикулярними). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Нульовий вектор вважається ортогональним до будь-якого вектора. |
|||||||||||||||||||||||||||||||||||||||||||||||||
G |
Приклад 3.10. |
Знайти кут між векторами |
x = (−3, |
15, 1, |
−5) і |
|||||||||||||||||||||||||||||||||||||||||||||
y = (1, −5, −2, 10). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
► Знайдемо норми векторів: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
xG |
|
|
|
|
|
= |
x2 |
+ x2 |
+ x2 |
+ x2 |
= |
(−3)2 +152 |
+12 |
+ (−5)2 = |
260, |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
yG |
|
|
|
|
|
= |
y2 |
+ y2 |
+ y2 |
+ y2 |
= |
|
12 + (−5)2 |
+ (−2)2 +102 = |
130. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
За формулою (3.47) знайдемо косинус кута φ між векторами: |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
|
(−3) |
1 +15 (−5) +1 (−2) + (−5) 10 |
|
1 |
|
|
3 |
|
|||||||||||||||||||||||||||
cosϕ = |
|
|
(Gx, |
yG) |
|
= |
= − |
, |
ϕ = |
π. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
260 130 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема Піфагора. Якщо вектори x і |
y ортогональні, то |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xG + yG |
|
|
|
2 = |
|
|
|
xG |
|
|
|
2 + |
|
|
|
y |
|
|
|
2 |
|
|
|
|
(3.48) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z ОбчислимоGквадратG норми суми векторів з урахуванням умови ортогональності (x, y) = 0:

 xG+ yG
xG+ yG
 2 = (xG+ yG, xG+ yG) = (xG, xG) +2(xG, yG) +( yG, yG) =
2 = (xG+ yG, xG+ yG) = (xG, xG) +2(xG, yG) +( yG, yG) = 
 xG
xG
 2 +
2 + 
 y
y
 2 .
2 .
Система векторів qG1 , q2 ,…, qn |
називається ортогональною, якщо |
|
(qGi , qGk )= 0 при i ≠ k і (qGi , qk )≠ 0 при i = k. |
|
|
G |
|
|
Системавекторів q1 , q2 ,…, qn називаєтьсяортонормованою, якщо: |
||
(qGi , qGk )= 0 |
i ≠ k . |
(3.49) |
1 |
i = k |
|
Приклад ортонормованого базису: e1, |
e2 , ..., en . |
|
Питання для самоперевірки
1.Чи може належати до базису нульовий вектор?
2.Із скількох векторів складається базис:
а) на прямій;
б) на площині; в) у просторі R3?
3. Чи є лінійно незалежними три вектори:
а) на площині; б) у просторі R3?
ДВНЗ “Українська академія банківської справи НБУ”
60
