Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет биоресурсов и природопользования

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Dolhikh_1

.pdf

Скачиваний:

Добавлен:

01.05.2015

Размер:

1.08 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

2. Розв’яжіть системи рівнянь двома способами:
а) методом Гаусса;																		б) методом Жордана-Гаусса.
		x + 2x				2	+ x		3				= 4,						2 x1 + 7 x2 + 3 x3 + x4 = 5,
		1				2			3
1)	3x		−5x				+ 3x							=1,							+ 3 x2		+ 5 x3		− 2 x4 = 3,
1)	3x		−5x			2	+ 3x					3		=1,				2)	x1		+ 3 x2		+ 5 x3		− 2 x4 = 3,
		1				2						3						2)	x		+ 5 x		− 9 x		+ 8 x		= 1,
		2x1	+ 7x2 − x3 = 8.																x	1	+ 5 x	2	− 9 x	3	+ 8 x	4	= 1,
		2x1	+ 7x2 − x3 = 8.																	1		2		3		4

																			5 x1 +18 x2 + 4 x3 + 5 x4 = 12 .
	2 x1 + 3x2 +11x3 + 5 x4 = 2,
3)		x	+ x		2		+ 5 x				3			+ 2 x			4	= 1,
3)		1			2						3						4
		2 x	+ x				+ 3x						+ 2 x					= −3,
		2 x	+ x		2		+ 3x			3			+ 2 x			4		= −3,
		1			2					3						4
	x + x			2	+		3x	3		+				4 x	4		= −3.
		1		2				3							4

3.Дослідіть системи рівнянь на сумісність. Для сумісних систем знайдіть загальний розв’язок.

x1 − x 2 + x3 − x 4 = −3,

x1 − 2 x2 + 3x3 + x4 = 1,

а)

2 x

− 3 x

− 4 x

+ x

= 1,

б)

2 x

+ x

+ 7 x

− x

= 5,

+ 7 x3 − 4 x 4 = −10 .

−

7 x

2 x

4 x

= 3.

x1 + 2 x 2 + 3 x3 − x 4 = 0,

x1 + 2 x 2

− 3 x4 + 2 x5 = 1,

в)

x1 − x 2 + x3 + 2 x 4 = 4,

г)

x1 − x2 − 3 x3 + x 4 − 3 x5 = 2,

2 x1 − 3 x2 + 4 x3 − 5 x 4 + 2 x5 = 7,

x1 + 5 x 2 + 5 x3 − 4 x 4 = −4,

x1 + 8 x 2 + 7 x 3 − 7 x 4 = −8 .

9 x1 − 9 x2 + 6 x3 − 16 x 4 + 2 x5 = 25 .

4. Знайдіть загальний розв’язок систем однорідних рівнянь:

2 x1 + x2 − x3 = 0,

б)

3 x1 − x 2 + 4 x 3 = 0,

а)

− x1 + 5 x 2 − x 4 = 0,

x1 + 2 x2 + x3 = 0,

2 x1 − x2 + 3x3 = 0.

3 x

+ 4 x

+ 3 x

= 0 .

3 x1 + x2 − 8 x3 + x4 = 0,

в)

2 x1 − 2 x2 − 3 x3 + 2 x4 = 0,

x1 + 11 x2 −12 x3 − 5 x4 = 0,

x1 − 5 x2 + 2 x3 + 3 x4 = 0.

5. Визначте значення параметра а, при якому система рівнянь має

ненульові розв’язки, і знайдіть їх.

ax1 + x2 + x3					=1,	2 x1 + x2 + 3x3 = 0,
а) x1 + ax2 + x3 =1,						б) 4 x1 − x2			+ 7 x3 = 0,
x	+ x	2	+ ax	3	=1.	x	+ ax	2	+ 2 x	3	= 0.
1						1

ДВНЗ “Українська академія банківської справи НБУ”

3. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ

Вектор − одне з основних понять, що застосовується в математиці та математичній економіці. Нижче розглядаються вектори у звичайному просторі, які можна зобразити графічно, а також n-вимірні вектори.

3.1. ОСНОВНІ ОЗНАЧЕННЯ

Вектор AB – це напрямлений відрізок із початком у точці А і кінцем у точці В. Вектори позначаються як двома великими літерами,

так і однією малою зі стрілкою, наприклад, AB, aG (рис. 3.1).

	a	a	b
AB	a		cG
AB			cG
A		aG =b = cG
		aG =b = cG
Рис. 3.1. Зображення			Рис. 3.2. Рівні вектори
й позначення векторів
Довжиною (модулем) вектора		AB називається довжина відрізка

АВ (позначається | AB |). Якщо початок вектора збігається з його кін-

цем, то вектор називається нульовим і позначається 0G. Напрям нульо-

вого вектора невизначений.

Вектор одиничної довжини називається одиничним вектором, або

ортом.

Вектори, які лежать на одній прямій або на паралельних прямих,

називаються колінеарними.

Колінеарність позначають символом ||: a ||b .

Вектори, які паралельні одній площині, називаються компланар-

ними.

Вектори називаються рівними, якщо вони колінеарні, мають однакові довжини та однакові напрями (рис. 3.2).

ДВНЗ “Українська академія банківської справи НБУ”

3.2.ЛІНІЙНІ ОПЕРАЦІЇ НАД ВЕКТОРАМИ

ВГЕОМЕТРИЧНІЙ ФОРМІ

Під лінійними операціями над векторами мають на увазі			опера-
цію множення вектора на число й операцію додавання векторів.
G	Добутком вектора aG на
λa (λ > 0)	число	λ називається	вектор
aG	b = λaG	з довжиною \| bG\|=\| λ \|\| aG\|

λaG (λ < 0)

Рис. 3.3. Множення вектора на скаляр

і напрямом, який збігаєтьсяG з

напрямом вектора a приGλ > 0, і протилежним напряму a при

λ < 0 (рис. 3.3).

	Властивості операції множення вектора на число
1)	(λ + β)aG = λaG+ βaG	(дистрибутивна властивість);
2)	λ(βaG) = (λβ)aG	(асоціативна властивість).
Сумою векторів aG і b		називається вектор cG = aG+b , початок Gяко-
го збігається з початком вектора a , а кінець − з кінцем вектора b			за

умови, що початок вектора bG збігається з кінцем вектора aG (правило

трикутника (рис. 3.4)). Вектор c у цьому випадку є діагоналлю пара-

лелограма, побудованого на векторах a і b (правило паралелограма).

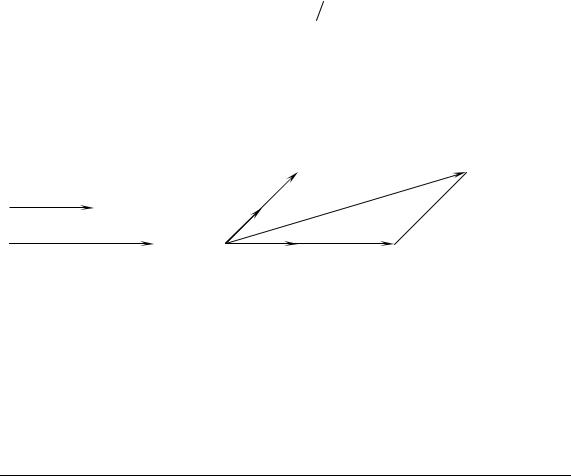
Додавання кількох векторів здійснюється за правилом замикання лан-

цюжка векторів (правило многокутника (рис. 3.5)).

Правило паралелограма Правило трикутника Правило многокутника

G	G	G	G	aG	b			b	cG
a	G	G	G		cG = aG + b			aG + b + cG + d
G	c	= a + b			cG = aG + b		a	aG + b + cG + d		G
b										d
Рис. 3.4. Додавання двох векторів							Рис. 3.5. Додавання
							кількох векторів
Різницею двох векторів a і b						називається сума вектора aG			й век-
тора (−b ), протилежного вектору b (рис. 3.6):
			aG	– b = a + (–b ).					(3.1)
		G	G	G	a	a	G	G
		c	= a −b		a	a	c	= a −b
	−bG				b		b

Рис. 3.6. Різниця двох векторів

ДВНЗ “Українська академія банківської справи НБУ”

	G		Властивості операції додавання векторів
1)			G	G	(комутативна властивість);
	a	+b = b + a
2)	(aG		+b) +cG	= aG+(b +cG)	(асоціативна властивість);

3)aG + 0 = aG;

4)aG + (−aG) = 0.

3.3. ЛІНІЙНА НЕЗАЛЕЖНІСТЬ ВЕКТОРІВ

Вираз виду c1a1 + c2 a2 +... + cn an , де c1 , c2 ,..., cn – числа, назива-

ється лінійною комбінацією векторів a1, a2 ,..., an .

Вектори aG1, aG2 ,..., aGn називаються лінійно незалежними, якщо їх

лінійна комбінація дорівнює нулю тільки тоді, коли c1 = c2 =…= cn = 0:

c1aG1 +c2aG2 +... +cnaGn = 0 c1 = c2 =... = cn = 0.

(3.2)

Якщо в (3.2) хоча б одне із чисел сk ≠ 0, то вектори a1, a2 ,..., an

називаються лінійно залежними. У цьому випадку принаймні один із векторів можна подати у вигляді лінійної комбінації інших, напри-

клад, якщо с1 ≠ 0, то:
aG1 = λ2aG2 +... + λnan , λi = −ci c1 (i = 2, 3,..., n) .	(3.3)

Максимальна кількість лінійно незалежних векторів простору на-

зивається розмірністю простору.

Істинні такі твердження:

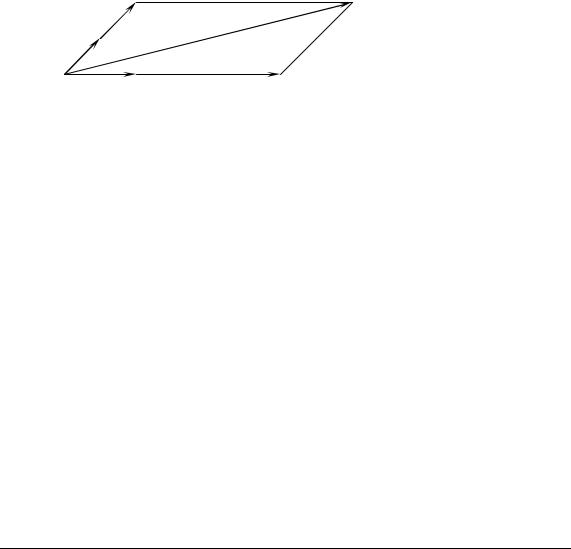
1.Будь-які два колінеарні вектори лінійно залежні (рис. 3.7).

2.Будь-які три компланарні вектори лінійно залежні (рис. 3.8).

3.Будь-які чотири вектори у трьохвимірному просторі лінійно залежні.

aG	λ2c		G	G
	λ2c		G	G
			a	= λ1b + λ2c
b = λaG	c
	b	λ1b
Рис. 3.7		Рис. 3.8

3.4. БАЗИС. РОЗКЛАДАННЯ ВЕКТОРА ЗА БАЗИСОМ

Упорядкована сукупність n лінійно незалежних векторів n-вимірного простору утворює його базис.

Базисом на прямій (у R1) називається будь-який ненульовий вектор. Базисом на площині (у R2) називаються два неколінеарні вектори,

взяті у визначеному порядку.

ДВНЗ “Українська академія банківської справи НБУ”

2eG2

Базисом у трьохвимірному просторі (у R3) називаються три не-

компланарні вектори, взяті у визначеному порядку.

Якщо кути між базисними векторами довільні, базис називають дові-

льним і позначають базисні вектори e1, e2 , e3 . Якщо базисні вектори взає-

мноперпендикулярніG (ортогональні), базисназиваютьортогональним. Якщо вектор a поданий у вигляді лінійної комбінації базисних

векторів:

a = c1e1 + c2e2 + c3e3 ,

(3.4)

то

кажуть,

що

він

розкладений за базисом

e1 , e2 , e3 . Вектори

c eG

, c

називають складовими (компонентами) вектора aG, а

− його координатами в базисі e1 , e2 , e3 . Звичайно пи-

числа c1 , c2 , c3

шуть так: aG

= (c , c

, c

a за базисом

На рис. 3.9 наведено приклад розкладу вектора

e , e

1 G2

Координатамивектора a єчисла(3, 2), аскладовими− вектори 3e1

і 2e2.

a =3e1 + 2e2 = (3, 2)

3e1

Рис. 3.9. Розклад вектора a за базисом e1, e2

Лінійні операції над векторами в координатній формі

Нехай у базисі eG1, eG2 , eG3 дані вектори:

aG = a1eG1 + a2eG2 + a3eG3 = (a1,a2 ,a3 ),							b =b1eG1 + b2eG2 + b3eG3 = (b1,b2 ,b3 ) .
Тоді лінійні операції визначаються так:
aG±b =(a ±b )eG			+(a ±b )eG +(a ±b )eG						=(a ±b , a ±b , a ±b ),
1	1	1	2	2	2	3	3	3	1	1	2	2	3	3
		λa =λa1e1 +λa2e2 +λa3e3 =(λa1,λa2,λa3).												(3.5)
Приклад 3.1. Визначити, чи є лінійно залежними вектори:
	a = (2, –1, 2), b = (1, 2, –3), с= (3, –4, 7).
► Вектори лінійно залежні, якщо існують такі одночасно не рівні
нулю числа c1,	c2,	c3, що c1aG + c2b + c3cG = 0 . Виконаємо операції над
векторами:

c1(2,–1, 2) + c2(1, 2, –3) + c3(3, –4, 7) = (0, 0, 0)

(2c1 + c2 + 3c3, –c1 + 2c2 – 4c3, 2c1 – 3c2 + 7c3) = (0, 0, 0).

ДВНЗ “Українська академія банківської справи НБУ”

З останньої рівності отримаємо систему лінійних однорідних рів-

нянь:

2c + c			+3c =0,		2	1	3

	1	2	3
−c1 + 2c2 − 4c3 =0,				=	−1	2	−4	=28−8 +9 −(12−7 +24) =0.
		−3c2 + 7c3 =0.			2 −3 7
2c1

Однорідна система має ненульові розв’язки, якщо її визначник дорівнює нулю. Отже, вектори лінійно залежні.

Приклад 3.2. Показати, що вектори a = (1, 2, 2), b = (−2, 1, 0),

с= (−3, −1, −1) утворюють базис у R3 і знайти координати вектора d =

= (−2, 1, 1) у цьому базисі.

► Вектори aG, b , сG утворюють базис, якщо вони лінійно незалежні, тобто якщо рівність c1aG + c2b + c3cG = 0 можлива лише при c1 = c2 =

= c3 = 0.

У даному випадку приходимо до системи лінійних однорідних

рівнянь:
c1 −2c2 −3c3 =0,			1	−2 −3

	+c2 −c3 =0,	=	2	1	−1	=5 ≠0.
2c1
	+0c2 −c3 =0,		2	0	−1
2c1

Оскільки визначник не дорівнює нулю − система має лише ну-

льовий розв’язок, вектори a , b ,								с лінійно незалежні й утворюють ба-
зис у просторі R3.															G			G				G
Розкладемо вектор d за базисом a , b , с															G			G	+ x			G
Розкладемо вектор d за базисом a , b , с													: d = x a + x				2	b	+ x	3		c
														1			2			3
x −2x −3x =−2,					1		−2	−3		−2				1 −8					−3				−2
x −2x −3x =−2,					1		−2	−3		−2				1 −8					−3				−2
1	2		3								~ e2		−2e1
2x1 + x2 − x3 =1,						2 1		−1		1	~ e2		−2e1	~	0 5						5		5	~
	+0x2 − x3 =1.					2 0		−1		1		e3	−2e1		0 4						5		5
2x1	+0x2 − x3 =1.					2 0		−1		1		e3	−2e1		0 4						5		5
		1 −8 −3		−2		e +8e			1 0 5			6	e −5e		1 0 0						1
		1 −8 −3		−2		e +8e			1 0 5			6	e −5e		1 0 0						1
						1	2						1	3
~ e2 /5 ~		0 1 1		1	~			~	0 1 1			1	~ e2 −e3		~	0 1 0					0
		0 4 5		5		e −4e			0 0 1			1				0 0 1					1
						3	2

x1 = 1, x2 = 0, x3 = 1 d = aG + 0b + cG.

ДВНЗ “Українська академія банківської справи НБУ”

3.5. АФІННА СИСТЕМА КООРДИНАТ

АфіннаG G Gсистема координат у просторі визначається завданням базису e1 , e2 , e3 і деякої точки O, яка називається початком координат.

Вектор OM =αeG + βeG		+γeG		називаютьрадіусом-векторомточкиM,
1	2		3
а числа α, β, γ − афінними координатами точки M і записують це так:
M(α, β, γ).	eG	, eG	, e		дано точки	M		(α	, β		,γ		) і
Якщо в базисі				3			1			1		1
	1	2						1

M 2 (α2 , β2 ,γ2 ) , то для того, щоб знайти координати вектора M1M 2 ,

необхідно від координат кінця вектора відняти координати його початку:

M1M 2 = OM 2 −OM1 = (α2 −α1, β2 −β1, γ2 −γ1).

(3.6)

3.6. ПРОЕКЦІЯ ВЕКТОРА НА ВІСЬ

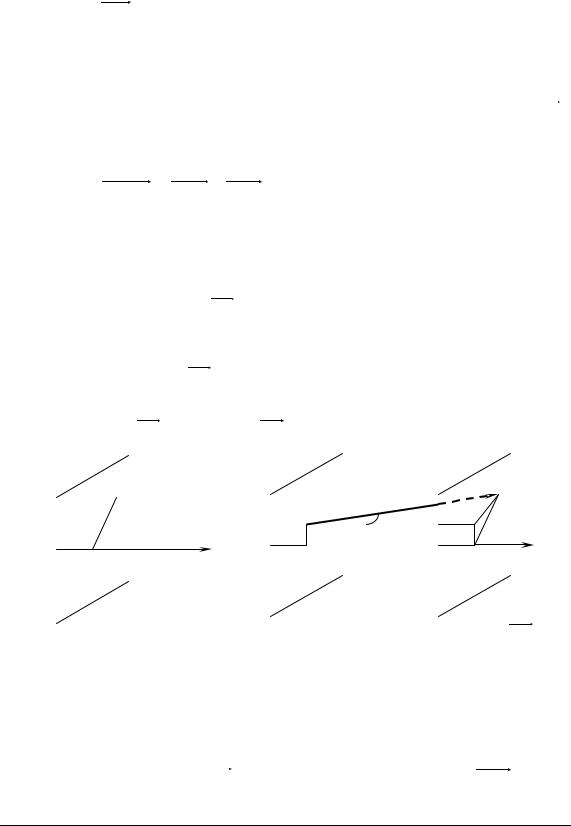
Проекцією точки А на вісь L називається основа перпендикуляра (точка Аl), опущеного з точки А на дану вісь (рис. 3.10).

Проекцією вектора AB на вісь L називається число, яке дорівнює різниці координат (xВ − xА) проекцій на вісь L кінця й початку вектора (рис. 3.11).

Проекція вектора AB на вісь L дорівнює добутку довжини векто-

ра на косинус кута ϕ між вектором та віссю:

ПрL AB = xB − xA =

cosϕ, 0 ≤ϕ ≤π.

(3.7)

Рис. 3.11. Проекція вектора AB

Рис. 3.10. Точка А1 − проек-

ція точки А на вісь L

на вісь L

Властивості проекції вектора на вісь

1)ПрL (aGG+ b + cG)G= ПрLaG + ПрLb + ПрLcG;

2)ПрLλa = λПрLa.

Складовою вектора AB на вісь L називається вектор A1B1 , де A1, B1 − проекції точок A і B на вісь L.

ДВНЗ “Українська академія банківської справи НБУ”

3.7. ВЕКТОРИ В ОРТОНОРМОВАНОМУ БАЗИСІ. ДЕКАРТОВА ПРЯМОКУТНА СИСТЕМА КООРДИНАТ

Базис, утворений трійкою взаємно перпендикулярних одиничних векторів, називається ортонормованим базисом. Афінна система координат, що пов’язана з ортонормованим базисом, називається декар-

товою прямокутною системою координат. Її базисні GвекториG G , що пов’язані з осями Ox, Oy, Oz, позначають відповідно так: i , j, k . Якщо

ax , ay , az – координати вектора a в базисі i , j, k , то:
aG = axiG + ay j + az k = (ax ,ay ,az ).	(3.8)

Нехай в базисі iG, Gj , k задані координати початку й кінця векто-

ра AB : А(х1, у1, z1), В(x2, y2, z2) (рис. 3.12), тоді

AB = OB –OA = (х2 – х1) iG+(у2 – у1) j +(z2 – z1) k =(х2 – х1, у2 – у1, z2 – z1), (3.9)

тобто, для того щоб знайти координати вектора AB , необхідно від ко-

ординат кінця вектора відняти відповідні координати його початку.

Рис. 3.12. Розкладання вектора AB за базисом i , j, k

Оскільки Прx AB = x2 − x1, Прy AB = y2 − y1, Прz AB = z2 − z1, то з

(3.9) випливає, що в ортонормованому базисі проекції вектора на осі співпадають з його координатами.

		Лінійні операції над векторами в базисі iG, Gj, kG
	Лінійні операції над векторами aG = axi + ay j + az kG		= (ax ,ay ,az ),
bG	=bxiG	+ by Gj + bz kG = (bx ,by ,bz ) визначаються так:
		λaG = λaxiG + λay j + λaz k = (λax ,λay ,λaz ),	(3.10)

aG±bG=(ax ±bx )iG+(ay ±by ) j +(az ±bz )k =(ax ±bx , ay ±by , az ±bz ). (3.11)

ДВНЗ “Українська академія банківської справи НБУ”

3.8. НАПРЯМНІ КОСИНУСИ ВЕКТОРА

Напрямними

косинусами вектора

a = (ax , ay , az ) називаються

косинуси

кутів α, β, γ, які утворює вектор з коор-

динатними осями (рис. 3.13):

cosα =

, cosβ =

, cosγ =

. (3.12)

Напрямні косинуси задовольняють

Рис. 3.13

умову:

cos 2 α + cos 2 β + cos 2 γ =1.

(3.13)

Координати одиничного вектора (орта) є його напрямними коси-

нусами:

= (cosα,cos β,cosγ ).

(3.14)

3.9. ПОДІЛ ВІДРІЗКА В ЗАДАНОМУ ВІДНОШЕННІ

Визначимо координати точки M(x, y, z), яка поділяє відрізок M1M2

у відношенні λ = M1M/MM2, якщо M1(x1, y1, z1), M2(x2, y2, z2) (рис. 3.14).

	M1M	M 2 (x2 , y2 , z2 )		M 2
λ =
	MM 2	M (x, y, z)	M	M1M = λMM 2

M1(x1, y1, z1) M1

Рис. 3.14. Поділ відрізка в заданому відношенні

Вектори M1M и MM 2			колінеарні. За умовою M1M =λMM2 , тобто
( x − x1 , y − y1 , z − z1 ) = λ( x2 − x , y2 − y , z2 − z ).
Прирівнявши відповідні координати, знаходимо:
x − x1 = λ ( x2 − x ),			y − y1 = λ ( y2 − y ),				z − z1 = λ ( z2 − z ).
Звідси знаходимо координати точки M:
x =	x1 + λx2	,	y =	y1 + λy2	,	z =	z1 + λz2	.	(3.15)

	1 + λ			1 + λ			1 + λ

ДВНЗ “Українська академія банківської справи НБУ”

З формул (3.15) при λ = 1 знайдемо координати середини відрізка M1M2:

x =	x1 + x2	,	y =	y1 + y2	,	z =	z1 + z2	.	(3.16)
				2
	2						2

Приклад 3.3. Знайти координати точки перетину медіан трикутни-

ка з вершинами A(xA , yA , zA ), B(xB , yB , zB ), C(xC , yC , zC ).

► Знайдемо координати точки D − середини відрізка BC:

xB + xC

, yD =

yB + yC

zD =

zB + zC

Медіани трикутника перетинаються в точці М, яка поділяє відрі-

зок АD у відношенні λ = AM/MD = 2/1. Знаходимо координати точ-

ки М:

xA + xB + xC

yA + yB + yC

xA + λxD

xA + 2xD

, yM

yA + λyD

1 + λ

1 + 2

1 + λ

zM =

z A + λzD

z A + zB + zC

1 + λ

3.10. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ

Скалярним добутком aG b двох векторів a і b

називається чис-

ло,

що дорівнює добутку довжин векторів на косинус кута ϕ між

ними:

cosϕ

(0 ≤ϕ ≤π) .

(3.17)

a b =

Алгебраїчні властивості скалярного добутку

(комутативна властивість);

aG b

=K b

Ga G

(a + b) c = a

+ b

(дистрибутивна властивість);

(асоціативна властивість);

(λa) b = λ(a b)

aG aG = aG2 =| aG|2 ≥ 0 −

скалярний квадрат вектора (aG aG=0 тільки

при | a|=0).

Геометричні властивості скалярного добутку

b = 0 aG

(умова перпендикулярності векторів);

> 0 ϕ

–

гострий кут;

< 0 ϕ

–

тупий кут.

ДВНЗ “Українська академія банківської справи НБУ”

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.04.2019872.96 Кб4Dictionary_culture_2011 1.doc
#
29.04.20192.62 Mб19Dictionary_culture_2011 2.doc
#
01.05.2015392.7 Кб6Dodatki_1-6_Pidsumkovi_Tablitsi_Vipiska_List-P.doc
#
02.05.2019616.96 Кб8Dodatok2.doc
#
01.05.201564.51 Кб10Dodatok_Nakaz_pro_obl_pol.doc
#
01.05.20151.08 Mб7Dolhikh_1.pdf
#
01.05.2015220.67 Кб5Dovidki_dodatki_7-19.doc
#
01.05.201511.99 Mб424Dpa matematika 2014.pdf
#
01.05.2015950.54 Кб10dudarev.docx
#
01.05.20151.56 Mб4Duglas_Distsiplinirovannyy_treyder.pdf
#
01.05.20157.97 Mб53EAS_ostatochny_variant.doc