2. Середня помилка вибірки

Помилки вибірки залежать насамперед від обсягу вибірки. Чим більше взято одиниць для вибірки, тим менша помилка. Якщо довести чисельність вибірки до чисельності одиниць генеральної сукупності , то дані вибіркової сукупності дорівнюватимуть даним генеральної сукупності.

Помилки вибірки, крім того, залежать і від варіації, коливання ознаки в сукупності. Чим більша варіація, тим більша помилка, і навпаки. Наприклад, якби всі 2000 продавців одержали зарплату 300 грн., то помилки не було б, бо середня заробітна плата у вибірковій сукупності була б такою самою, як і в генеральній. На практиці цього не буває, бо зазвичай є відхилення.

Щоб оцінити, наскільки зведені показники вибіркової сукупності відрізняються від генеральної, потрібно обчислити не просто помилку вибірки, а середню помилку вибірки.

Чому середню? Перш за все тому, що з будь-якої сукупності можна провести не одну, а багато вибірок, і їх зведені результати зазвичай не збігаються, хоча й близькі.

Таблиця 1

Розподіл студентів факультету за успішністю

Оцінка	Чисельність студентів				Сума одержаних балів
	Генеральна сукупність	Вибіркова сукупність			Генеральна сукупність		Вибіркова сукупність
x	N	n1	n2	xN		xn1		xn2
2	50	8	6	100		16		12
3	750	185	136	2250		555		408
4	1000	170	210	4000		680		840
5	200	37	48	1000		185		240
Усього	2000	400	400	7350		1436		1500

Обчислимо середню успішність студентів у генеральній і вибірковій сукупностях (середній бал). Середня успішність студентів у генеральній сукупності

а середня успішність у першій і другій вибіркових сукупностях — відповідно

Зазвичай після кожної вибірки її помилка набуває різних значень:

Обчислимо тепер частку студентів у генеральній і вибірковій сукупностях, які навчаються на "4" та "5":

Як бачимо, помилки вибірки для частки також різні:

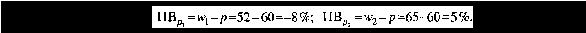
Оскільки помилки вибірки — змінні величини, що можуть набувати різних значень залежно від чисельності вибірки та варіації ознак, остільки виникає потреба в обчисленні середньої помилки вибірки.

Вибірка може бути повторною та безповторною.

Повторною називається вибірка, коли одиниці, що вже один раз потрапили у вибірку, повертають у генеральну сукупність, і вони можуть знову бути у вибірці кілька разів. Наприклад, усі громадяни формально можуть одержати путівку в санаторій, а отримують часто одні й ті самі. Те саме можна сказати про відвідування магазину, театру, обмін валют, поїздки за кордон тощо.

Безповторною називається вибірка, коли один раз відібрані одиниці для обстеження не повертають знову в генеральну сукупність, і вони не беруть участі в подальших відборах (наприклад, розіграш лотереї, народження людини, її смерть тощо).

У разі безповторної вибірки помилки репрезентативності менші, ніж у разі повторної.

Для визначення середньої помилки вибірки для середньої та частки в разі повторної вибірки користуються такими формулами:

у разі безповторної -

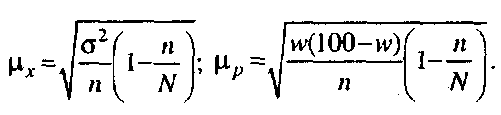
У математичній статистиці доведено, що значення середньої помилки вибірки визначають за допомогою залежності

за умови, що відома генеральна дисперсія. Але в разі проведення вибіркового обстеження ці показники зазвичай невідомі. Тому на практиці використовують дисперсію вибіркової сукупності. При цьому виходять із того, що в разі застосування принципу випадкового відбору дисперсія достатньо великого обсягу вибірки практично збігається з дисперсією генеральної сукупності. У математичній ста-тистиці доведено таке співвідношення між дисперсіями в генеральній і вибірковій сукупностях:

Згідно з ним дисперсія у вибірковій сукупності менша, ніж дисперсія в генеральній, в разів. Зі збільшеннямвідношення наближається до одиниці, а — до Якщо замінити генеральну дисперсію вибірковою, то

Для показника середньої величини дисперсії кількісної ознаки у вибірці визначають за такими залежностями:

де— частота.

Середня помилка вибірки показує, наскільки в середньому вибіркова середня величина (частка) відрізняється від генеральної. її обчислюють для того, щоб перенести результати вибірки на генеральну сукупність за допомогою формул

Продемонструємо обчислення середньої помилки вибірки та перенесемо результати на генеральну сукупність.

Нехай =303 грн; =2000; =200; =30 грн; = 82

Обчислимо середню помилку вибірки для середньої зарплати за формулою повторної вибірки:

і безповторної:

Отже, середня заробітна плата у вибірковій сукупності відрізняється від генеральної на 2,12 грн. в разі повторної вибірки та на 2,01 грн. — у разі безповторної.

Перенесемо результати вибіркового спостереження на генеральну сукупність: . У разі повторної вибірки, а в разі без повторної.

Отже, середня заробітна плата продавця в генеральній сукупності лежить у межах від 300,88 до 305,12 грн. в разі повторної вибірки та в межах від 300,99 до 305,01 грн. — у разі безповторної.

Обчислимо середню помилку вибірки для частки продавців зі спеціальною освітою за формулою повторної вибірки:

і безповторної:

Отже, під час визначення частки продавців зі спеціальною освітою допущено помилку 2,7 % у разі повторної вибірки та 2,6 % — у разі безповторної.

Перенесемо результати вибіркового спостереження на генеральну сукупність: . У разі повторної вибірки, а в разі безповторної —

Отже, частка продавців зі спеціальною освітою в генеральній сукупності лежить у межах від 79,3 до 84,7 % у разі повторної вибірки, та в межах від 79,4 до 84,6 % — у разі безповторної.

Математична статистика гарантує такі висновки щодо середньої заробітної плати та частки продавців зі спеціальною освітою лише з імовірністю 0,683 (див. підрозд. 9.3). Якщо дослідника влаштовує така ймовірність, обчислення завершують, а не то визначають так звану граничну помилку вибірки, що залежить від коефіцієнта довіри, кожному значенню якого відповідає конкретний показник імовірності.