1. Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой)точности измерения. а) неустранимые: 1, погрешность исходных данных, 2. Погрешность математической модели. б)полные: 1. Неустранимая, 2.Метода, 3.Вычислительная. В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы. Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

Абсолютная погрешность — является оценкой абсолютной ошибки измерения Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или среднему значению измеряемой величины (РМГ 29-99): , . Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора. Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики. Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях. Систематическая погрешность — погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором. Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс. Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры 

2. Основная задача теории погрешностей состоит в том, чтобы определить по известным погрешностям параметров погрешность функции от этих параметров. Пусть задана дифференцируемая функция и пусть- абсолютные погрешности аргументов. Тогда абсолютная погрешность функции (формула Лагранжа):

При зависимости функции от одного параметра:

Предельной абсолютной погрешностью функции называют следующую оценку погрешности величины :

Пусть задана дифференцируемая функция и пусть- относительные погрешности аргументов. Тогда относительная погрешность функции:

 или 

Предельной относительной погрешностью функции называю величину .

Рассмотрим частные случаи.

Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей слагаемых:

Формула дает максимально возможное значение предельной абсолютной погрешности суммы, которое достигается, если погрешность каждого слагаемого принимает наибольшее из возможных значений, и погрешности всех слагаемых имеют одинаковые знаки. При большом количестве слагаемых такое неблагоприятное стечение обстоятельств маловероятно. Погрешности отдельных слагаемых, как правило, имеют различные знаки и частично компенсируют друг друга.

Если все числа одного знака (арифметическая сумма), и относительная погрешность удовлетворяет неравенствустановится очевидным, что для повышения точности суммы в первую очередь необходимо уточнить слагаемые с наибольшей относительной погрешностью. (Андреев-8)

Остановимся на вычислении предельной относительной погрешности разности. Пусть и числаразных знаков, тогда:

При малой абсолютной погрешности близких чисел относительная погрешность их разности может быть весьма большой. Это явление называетсяпотерей точности при вычитании близких чисел.При приближенных вычислениях следует избегать вычитания близких чисел, преобразовывая выражения, приводящие к подобным операциям.

Погрешность степенного выражения расчитывается следующим образом:

Зная , предельную абсолютную погрешность можно найти по формуле.

Отметим несколько полезных следствий из полученной формулы:

1. Предельная относительная погрешность произведения равна сумме предельных относительных погрешностей сомножителей

2. ,. При умножении приближенного числа на точный множительпредельная относительная погрешность приближенного числа не меняется, а предельная абсолютная погрешность увеличивается враз \vartriangle _{y}.

3. ,. Предельная относительная погрешность степени приближенного числа умножается на показатель степени.

4. Предельная относительная погрешность корня из приближенного числа делится на показатель корня.

3. Обратная задача теории погрешностей и ее решение методом равных влияний

Обратная задача теории погрешностей состоит в том, чтобы определить с какой точностью необходимо задавать значения аргументов функции , чтобы ее погрешность не превосходила заданной величины? Эта задача математически неопределена, так как заданную погрешностьможно обеспечить при любом наборе предельных абсолютных погрешностей аргументов удовлетворяющих условию:

Простейшее решение обратной задачи дает принцип равных влияний, согласно кото- рому вклады всех аргументов в формирование абсолютной погрешности функции равны:

Отсюда

, где 

Иногда при решении обратной задачи по принципу равных влияний абсолютные погрешности отдельных аргументов оказываются настолько малыми, что вычислить или измерить эти величины с соответствующей точностью невозможно. В таком случае отступают от принципа равных влияний, чтобы увеличение погрешности одних переменных компенсировать уменьшением погрешности других.

Относительной погрешностью называют некоторую величину , про которую известно, что она удовлетворяет неравенству:

Относительную погрешность часто выражают в процентах. Она дает более точное представление о величине ошибки, содержащейся в некоторой величине.

Часть 2 1. Апроксимация – замена одной функции другой, более близкой к исходной и обладающей хорошими свойствами(лёгкость выполнения аналитических данных и вычислительных операций)

Простейшая задача интерполяции заключается в следующем. На отрезке [a, b] заданы n + 1 точки x_i = х₀, х₁, . . ., х_n, которые называютсяузлами интерполяции, и значения некоторой функции f(x)  в этих точках

f(x0) = y0, f(x1) =  y1,  . . ., f(xn) = yn.

(1)

Требуется построить функцию  (х) (интерполяционная функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т. е. такую, что

(x0) = y0, (x1) =  y1,  . . ., (xn) = yn.

(2)

Геометрически это означает, что нужно найти кривую y =  (х) некоторого определенного типа, проходящую через заданную систему точек M(x_i,y_i) (i = 0, 1, ..., n) (Рисунок 1).

  

В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь решений.

Однако эта задача становится однозначной, если вместо произвольной функции  (х) искать полином  (х) (интерполяционный полином) степени не выше n, удовлетворяющий условиям (2), т. е. такой, что

 (x0) = y0,  (x1) =  y1,  . . .,  (xn) = yn.

(3)

Полученную интерполяционную формулу

(4)

обычно используют для приближенного вычисления значений данной функции  (х) для значений аргумента х, отличных от узлов интерполяции. Такая операция называется интерполяцией функций.

Различают два вида интерполяции:

1. глобальная - соединение всех точек  (х) единым интерполяционным полиномом;

2. локальная - соединение точек отрезками прямой (по двум точкам), отрезками параболы (по трем точкам).

2. Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x₀, y₀), (x₁,y₁),…, (x_n, y_n), где все x_j различны, существует единственный многочлен L(x) степени не более n, для которого L(x_j) = y_j. В простейшем случае (n=1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки. Лагранж предложил способ вычисления таких многочленов:

3. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики. ЭЙТКЕНА СХЕМА

- метод вычисления значения интерполяционного многочлена L_n(x)по узлам х ₀, х₁, . . ., х _п в точке х,основанный на последовательном применении формулы 

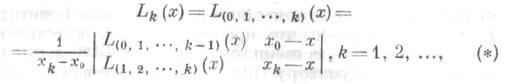
где L(i, i+1,.... m)(x)- интерполяционный многочлен с узлами интерполяции x_i, x_i+1, . . ., х _т, в частностиL_i(x)=f(x_i) (см. Интерполяционная формула). Процесс вычисления по формуле (*) можно закончить, когда взначениях двух интерполяционных многочленов последовательных степеней совпадает требуемоеколичество знаков. Э. с. удобно использовать для интерполяции значений таблично заданной функции,перенумеровав узлы интерполяции в порядке возрастания |x-x_i|.

4.

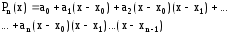
5. Классическим примером (Рунге), показывающим возникновение осцилляций у интерполяционного многочлена, служит интерполяция на равномерной сетке значений функции

Введем на отрезке равномерную сетку,,и рассмотрим поведение многочлена

который в точках принимает значения. На рисунке представлены графики самой функции (штрих-пунктирная линия) и трех интерполяционных кривых при:

• интерполяция на сетке 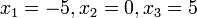— квадратичная парабола;

• интерполяция на сетке 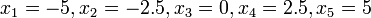— многочлен четвертой степени;

• интерполяция на сетке 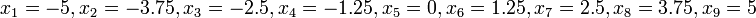— многочлен восьмой степени.

Значения интерполяционного многочлена даже для гладких функций в промежуточных точках могут сильно уклоняться от значений самой функции.

6.Экстраполя́ция, экстраполи́рование (от лат. extrā — вне, снаружи, за, кроме и лат. polire — приглаживаю, выправляю, изменяю, меняю^[1]) — особый тип аппроксимации, при которомфункция аппроксимируется вне заданного интервала, а не между заданными значениями.

Иными словами, экстраполяция — приближённое определение значений функции в точках, лежащих вне отрезка, по её значениям в точках.7. первая интер­поляционная формула Ньютона обычно используется для интерполирования вперёд и экстраполирования назад,  .    (3)

Это и есть обычный вид второй интерполяционной формулы Ньютона. Для прибли­жённого вычисления значений функции полагают:

.

8. Интерполяционная формула Гаусса — формула, использующая в качестве узлов интерполяции ближайшие к точке интерполирования x узлы. Если , то формула

написанная по узлам , называетсяформулой Гаусса для интерполирования вперед, а формула

написанная по узлам , называетсяформулой Гаусса для интерполирования назад. В формулах (1) и (2) использованы конечные разности, определяемые следующим образом:

Преимущество интерполяционной формулы Гаусса состоит в том, что указанный выбор узлов интерполяции обеспечивает наилучшую оценку остаточного члена по сравнению с любым другим выбором, а упорядоченность узлов по мере их близости к точке интерполяции уменьшает вычислительную погрешность интерполирования.

9. Аппроксимация экспериментальных данных в программе MathCAD

MathCAD — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением. MathCAD идеально подходит для осуществления математического моделирования — осуществляя решение разного рода уравнений и создавая отчет о полученных результатах.

В MathCAD совсем немного типов данных по сравнению с универсальными языками программирования — всего три. Кратко охарактеризуем их (более детально они будут описаны позже).

Числа (как действительные, так и комплексные): все числа MathCAD хранит в одном формате (с плавающей точкой двойной точности), не разделяя их на целые и действительные. На одно число выделяется 64 бита. При этом десятичная часть не может превышать по длине 17 знаков, а порядок должен лежать между –307 и 307. Комплексные числа на уровне реализации представляют собой пару действительных чисел. При этом во многих видах расчетов число воспринимается как комплексное, даже если у него нет мнимой части. Описанные особенности чисел в MathCAD касаются только численных расчетов. При работе в символьном режиме совершенно другие уровни точности.

Строки: в общем случае любой текст, заключенный в кавычки. На практике строки используются в основном для задания сообщений об ошибках, возникших при работе программ на языке MathCAD.

Массивы: к ним относятся матрицы, векторы, тензоры, таблицы — любые упорядоченные последовательности элементов произвольного типа. К данным этого типа можно отнести и ранжированные переменные. В отдельную группу следует выделить так называемые размерные переменные, то есть единицы измерения, имеющие огромное значение в науке и технике. В MathCAD нет логического типа данных. Для обозначения истины и лжи логическими операторами и функциями используются числа — 0 и 1.

В MathCAD существует несколько функций, позволяющих выполнить регрессию с использованием зависимостей, наиболее часто встречающихся на практике. Таких функций в MathCAD всего шесть. Вот некоторые из них:

· expfit(vx,vy,vg) - регрессия экспоненциальной функцией y = a*e^b*x+c.

· sinfit(vx,vy,vg) - регрессия синусоидальной функцией y = a*sin(x+b)+c.

· pwrfit(vx,vy,vg) - регрессия степенной функцией e = a*x^b +c.

Перечисленные функции используют трехпараметрическую аппроксимирующую функцию, нелинейную по параметрам. При вычислении оптимальных значений трех параметров регрессионной функции по методу наименьших квадратов возникает необходимость в решении сложной системы из трех нелинейных уравнений. Такая система часто может иметь несколько решений. Поэтому в функциях MathCAD, которые проводят регрессию трехпараметрическими зависимостями, введен дополнительный аргумент vg. Данный аргумент - это трехкомпонентный вектор, содержащий приблизительные значения параметров a,b и c, входящих в аппроксимирующую функцию. Неправильный выбор элементов вектора vg может привести к неудовлетворительному результату регрессии. В MathCAD существуют средства для проведения регрессии самого общего вида. Это означает, что можно использовать любые функции в качестве аппроксимирующих и находить оптимальные значения любых их параметров, как линейных, так и нелинейных. В том случае, если регрессионная функция является линейной по всем параметрам, т.е. представляет линейную комбинацию жестко заданных функций, провести регрессию можно с помощью встроенной функции linfit(vx,vy,F). Аргумент F - это векторная функция, из элементов которой должна быть построена линейная комбинация, наилучшим образом аппроксимирующая заданную последовательность точек. Результатом работы функции linfit является вектор линейных коэффициентов. Каждый элемент этого вектора - коэффициент при функции, стоящей на соответствующем месте в векторе F. Таким образом, для того чтобы получить регрессионную функцию, достаточно скалярно перемножить эти два вектора.

10. Линейная интерполяция

 

При линейной интерполяции MathCAD соединяет существующие точки данных прямыми линиями. Это выполняется функцией linterp.

linterp

Использует векторы данных и, чтобы возвратить интерполируемое значение, соответствующее третьему аргументу. Аргументыидолжны быть векторами одинаковой длины. Вектордолжен содержать вещественные значения, расположенные в порядке возрастания.

Эта функция соединяет точки данных отрезками прямых, создавая таким образом ломаную. Интерполируемое значение для конкретного х есть ордината у соответствующей точки ломаной.

Для значений , расположенных перед первой точкой в векторе, MathCAD продолжает ломаную прямой линией, проходящей через первые две точки данных. Для значений, расположенных за последней точкой, MathCAD продолжает ломаную прямой линией, проходящей через последние две точки данных.

Для получения наилучших результатов должно находится между самыми большими и самыми маленькими значениями- маловероятно, что будут полезны значения, вычисленные длявне этого диапазона. Функцияlinterp предназначена для интерполяции, а не для экстраполяции. Рисунок 5 показывает некоторые примеры линейной интерполяции.

Кубическая сплайн-интерполяция

 

Кубическая сплайн-интерполяция позволяет провести кривую через набор точек таким образом, что первые и вторые производные кривой непрерывны в каждой точке. Эта кривая образуется путем создания ряда кубических полиномов, проходящих через наборы из трех смежных точек. Кубические полиномы затем состыковываются друг с другом, чтобы образовать одну кривую.

MathCAD поставляется с тремя сплайн-функциями:

cspline

pspline

lspline

Они возвращают вектор коэффициентов вторых производных, который мы будем называть . Этот векторобычно используется в функцииinterp, описанной ниже. Аргументы идолжны быть вещественными векторами одинаковой длины. Значения векторадолжны быть расположены в порядке возрастания.

Эти три функции отличаются только граничными условиями:

• функция lspline генерирует кривую сплайна, которая приближается к прямой линии в граничных точках;

• функция pspline генерирует кривую сплайна, которая приближается к параболе в граничных точках.

• функция cspline генерирует кривую сплайна, которая может быть кубическим полиномом в граничных точках.

interp 

Возвращает интерполируемое значение , соответствующее аргументу. Векторвычисляется на основе векторов данныхиодной из функцийpspline, lspline или cspline.

Чтобы провести кубический сплайн через набор точек (Рисунок 6):

• создайте векторы 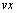и, содержащие координаты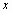и,через которые нужно провести кубический сплайн. Элементы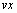должны быть расположены в порядке возрастания. (Хотя мы используем имена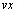,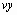и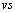, нет никаких ограничений на имена этих переменных; можно использовать любые имена);

• Вычислите вектор

.

Вектор содержит вторые производные интерполяционной кривой в рассматриваемых точках;

• чтобы найти интерполируемое значение в произвольной точке 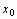, вычислитеinterp, где 

- векторы, описанные ранее.

  

Можно сделать то же самое, вычисляя: interp.

Интерполируемое значение для конкретного х есть ордината у соответствующей точки сплайна. Для значений , расположенных перед первой точкой вектора, MathCAD продолжает сплайн первой из составляющих его кубических парабол. Для значений, расположенных за последней точкой, MathCAD продолжает сплайн первой из составляющих его кубических парабол.

Для получения наилучших результатов должно находится между самыми большими и самыми маленькими значениями- маловероятно, что будут полезны значения, вычисленные длявне этого диапазона. Сплайны предназначены для интерполяции, а не для экстраполяции.

 

Интерполяция вектора точек

 

Можно использовать оператор векторизации, чтобы вычислить сразу целый набор интерполируемых значений, соответствующих вектору заданных точек. Это можно сделать и с interp, с и linter.

Пример 10 показывает, как выполнить эту операцию. Чтобы применить оператор векторизации к функции, щелкните мышью на имени функции и нажимайте клавишу пробел, пока в рамку не попадет нужная функция. Затем нажмите Ctrl + - (минус).

Пример 10. Кубическая сплайн-интерполяция

 

Линейное предсказание (экстраполяция)

 

Иногда необходимо оценить значения формул в точках, находящихся вне области расположения сетки, на которой заданы значения функции. В Mathcad есть функция predict, которая позволяет это сделать.

Эта функция использует линейный алгоритм предсказания, который является полезным, когда экстраполируемая функция является гладкой и осциллирующей, хотя не обязательно периодической. Линейное предсказание можно рассматривать как разновидность экстраполяции, но нельзя путать с линейной или полиномиальной экстраполяцией.

 

 

predict возвращает предсказанных значений, основанных наm последовательных значениях вектора данных . Элементы векторадолжны представлять собой значения, взятые через равные интервалы.

Функция predict использует последние m исходных значений данных, чтобы вычислять коэффициенты предсказания. Как только это сделано она использует последние m точек, чтобы предсказать координаты - ой точки, фактически создавая скользящее окно шириной вточек (Рисунок 7).

 

Двумерная сплайн-интерполяция

 

MathCAD выполняет интерполяцию кубическими сплайнами функции двух переменных тем же самым образом, как и в одномерном случае, обсужденном ранее. MathCAD проводит через сетку узлов поверхность, составленную из кубических полиномов от х до у, таким образом, что первые и вторые производные являются непрерывными в каждом узле сетки.

cspline

pspline

lspline

Они возвращают вектор коэффициентов вторых производных, который мы будем называть . Этот векторобычно используется в функцииinterp, описанной ниже. -n  2 матрица, чьи элементы Mxy_i, 0 и Mxy_i, 1, определяют точки на диагонали n  n сетки. (ij)-элемент n  nматрицы Mz определяет значение интерполирующей функции в (Mxy_i, 0, Mxy_j, 1).

Эти три функции отличаются только граничными условиями:

• функция lspline генерирует сплайн, который приближается к плоскости на краях сетки;

• функция pspline генерирует сплайн, который представляет полином второй степени от х и у на краях сетки;

• функция cspline генерирует сплайн, который представляет полином третьей степени от х и у на краях сетки.

interp 

Возвращает интерполируемое значение z, соответствующее точкам =v₀ и y = v₁. Вектор вычисляетсяpspline, lspline или cspline на основе векторов данных Mxy и Mz.

Первый шаг в двумерной сплайн-интерполяции - точно такой же, как и в одномерном случае: определить узлы, через которые поверхность должна пройти. Однако это потребует больше усилий, потому что теперь нужно определить сетку узлов:

• создайте n  2 матрицу Mxy, чьи элементы, Mxy_i, 0 и Mxy_i, 1 определяют х и у координаты по диагонали прямоугольной сетки. Эта матрица играет ту же самую роль, что и vx в одномерном случае, описанном ранее. Так как эти узлы описывают диагональ, элементы в каждом столбце Mxy должны быть расположены в порядке возрастания (Mxy_{i, k} < Mxy_{j, k} всякий раз, когда i < j);

• создайте n  n матрицу Mz, чей (ij)- элемент есть координата z соответствующая точке х = Mxy_i, 0 и у = Mxy_j, 1. Она играет ту же самую роль, что и vy в одномерном случае, описанном ранее;

• вычислите вектор

Вектор содержит вторые производные приближающей поверхности в узлах, определенныхMxy и Mz;

• чтобы найти интерполируемое значение в произвольной точке, скажем (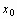,у₀), вычислите