14. Доверительный интервал для выборочного среднего. Анализ однородности выборки.

Доверительный интервал случаен (зависит от конкретных выборок): случайно его положение на числовой оси и случайна его длина.

При , а при

Доверительный интервал для оценки математического ожидания

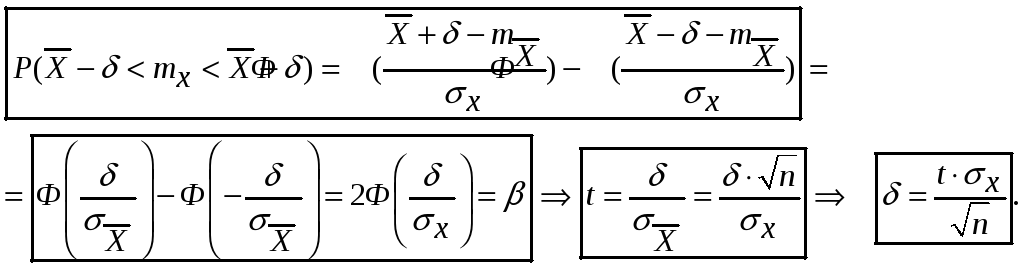
Здесь рассматривается как аргумент табулированной функции распределения Лапласа (нормальной !), при котором она равна значению : .

Значение генерального среднеквадратического отклонения редко известно, поэтому обычно в формуле используют оценку среднеквадратического отклонения, т.е. .

Пример:~ Найти доверительный интервал для оценки неизвестного , при выборочном среднем , если объем выборки n=36, а .

Замечание. Практически важной может быть задача определения объема выборки, которая обеспечит заданный радиус доверительного интервала: .

Более точные результаты при малых объемах выборки и неизвестном дает использование распределения Стьюдента: для переменной - , имеющей распределение Стьюдента с степенями свободы отклонение (~) Тогда доверительный интервал при неизвестном среднеквадратическом отклонении определяется следующим образом: , где аргумент табулированного распределения Стьюдента.

Доверительные интервалы оценки среднеквадратического отклонения

Пусть вновь ~, и - неизвестно, а . Тогда

где .

Доказано, что имеет табулированное распределение , независящее от параметров и исходного распределения, но зависящее от объема выборки и доверительной вероятности. Вычислив по выборке , находим по таблице , определяем границы доверительного интервала.

15. Проверка соответствия выборочных данных теоретическому распределению.

16. Дисконтирование денежных потоков.

Метод дисконтирования денежных потоков является ключевым в финансовом анализе. Рассмотрим этот метод на примере банковских депозитов. Обозначим:

P – начальный капитал, положенный в банк;

r – процентная ставка банка;

S – наращенная сумма.

Тогда в конце первого периода капитализации наращенная сумма составит:

.

Если эта сумма остается в банке, то в конце второго периода капитализации наращенная сумма составит:

.

В общем случае сумма, наращенная за n периодов капитализации, рассчитывается по формуле:

. (9.1)

В течение периода капитализации проценты могут начисляться несколько раз, тогда наращенная сумма будет увеличиваться.

На основании формулы (9.1) можно также найти, какой начальный капитал нужно положить в банк, чтобы наращенная за n периодов капитализации сумма составила заданную величину S. Такой начальный капитал называется текущей (приведенной) ценностью суммы S и обозначается PV:

. (9.2)

Процесс нахождения текущей ценности называется дисконтированием.

Пример 9.1. Годовая процентная ставка банка составляет 12%. Какую сумму нужно положить в банк, чтобы наращенная за пять лет сумма составила 1000 ден. единиц?

Решение. По условию r=0,12; n=5; S=1000. По формуле (9.2) найдем текущую ценность заданной суммы:

.

Таким образом, в банк следует положить 567,431 ден. ед.

На основании формулы (9.1) можно также решить задачу определения количества времени, требующегося для накопления определенной суммы.

Пример 9.2. Если положить в банк 1000 у.е. при годовой процентной ставке 10%, то через сколько лет накопленная сумма составит 2000 у.е.?

Решение. По условию даны следующие величины: P=1000; S=2000; r=0,1. Требуется найти количество временных периодов n. Запишем формулу (9.1): . Решив это уравнение относительно n, получим: n=7,27. Таким образом, на данное накопление потребуется больше семи лет.