11. Числовые характеристики случайной величины: математическое ожидание, дисперсия, среднеквадратическое отклонение, мода, медиана.

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности:

M(X) = x1p1 + x2p2 + ... + xnpn

Свойства математического ожидания.

1) Математическое ожидание постоянной величины равно самой величине:

М(С) = С

2) Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = С·М(Х)

3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

М(Х1 + Х2 + …+ Хn) = М(Х1) + М(Х2) + ... + М(Хn)

4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

М(Х1 · Х2 · ... · Хn) = М(Х1) · М(Х2) · ... · М(Хn)

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2

Свойства дисперсии.

1) Дисперсия постоянной величины равна нулю: D(С) = 0

2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2 · D(Х)

3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:

σ(X) = √D(X)

Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений и соответствующих им вероятностей:

Модой дискретной случайной величины, обозначаемой называется ее наиболее вероятное значение.

Медианой случайной величины называется такое ее значение , для которого одинаково вероятно, окажется ли случайная величина меньше или больше , т.е.

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения:

Дисперсия дискретной случайной величины вычисляется по формуле:

или

Средним квадратическим отклонением (стандартом) случайной величины называется арифметический корень из дисперсии, т.е.

12. Выборочный метод. Абсолютные и относительные частоты. Эмпирическая функция распределения. Полигон частот.

13. Выборочные оценки параметров распределения.

Оценка математического ожидания (выборочной средней):

Неслучайное математическое ожидание: 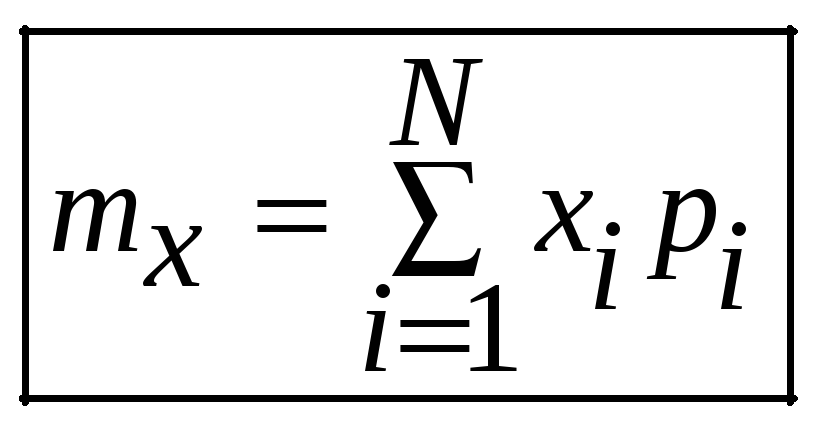- генеральная средняя

С.в. - оценка матожидания - выборочная средняя

, где частота отдельных значений

Так как

Оценка выборочной дисперсии:

- стандарт (выборочное стандартное –среднеквадратическое отклонение).

Удобная формула оценки дисперсии через оценку второго начального момента

Аналогично рассчитываются и другие выборочные оценки распределения

Точечные оценки точности оценок (статистик) генеральных числовых характеристик

-оценки статистических характеристик

- с.в., характеризуемая законами распределения и числовыми характеристиками распределения (обычно математическим ожиданием и дисперсией).

Можно говорить о распределении оценки матожидания, о матожидании оценки мат.ожидания, о дисперсии оценки мат.ожидания и т.д.

1. Оценка называется состоятельной, если она сходится по вероятности к оцениваемой характеристике.

2.Оценка называется несмещенной, если .

- смещение, систематическая погрешность (от смещенности)

Асимптотически несмещенная оценка

3.Оценка называется эффективной, если при используемом методе ее расчета выполняется условие .

Пример1. Оценка является несмещенной, а ее дисперсия уменьшается при усреднении в раз:

Если ~- эффективная оценка.

В прикладной статистике и в эконометрике, наибольшее внимание уделяют обеспечению эффективности и несмещенности оценок.

Пример 2. Оценка дисперсии является смещенной:

Доказано, что - т.е. данный алгоритм дает смещенную оценку дисперсии: . Исправленная (несмещенная) оценка дисперсии

.

На практике исправленной оценкой дисперсии пользуются при

Интервальная оценка точности (надежность) генеральных математического ожидания и дисперсии

Доверительный интервал - интервал значений, в котором с заданной доверительной вероятностью (обычно назначают ) находится истинное значение оцениваемой статистической характеристики : .

Радиус доверительного интервала равен:,

- аргумент, соответствующий значению функции Лапласа, равной :

; - среднеквадратическое отклонение (его оценка).