2.Статический и интервальный ряды распред-я.

Если представляет собой непрерывную случ. вел-ну и если количество k>10, то в этом случае для представления рез-тов исп-ется интервальный ряд распред-я.

V - число интервалов, приблизительно от 7 ло 11.

Ф-ла Стерджеса: R=max x_i - min x_i (R -размах)

h=R/V, где ,h - шаг.

x_k-1-h<x_k<=max x_i

Билет 27

2.Понятие временного ряда. Линейные, нелинейные тренды.

y_t=f(x_t,t)+ε_t

x_t-детерминированный фактор, ε_t-случ. вел-на мат.ожидания, к-рая равна 0.

Анализ временных рядов с целью прогнозирования поведения y_t (объем производства, прибыль). На эти временые показатели влияют случ. факторы, к-рые не поддаются точному анализу.

Линейный тренд. Если временной ряд имеет вид регрессивной зависимости: y_t=α₀ +Σ^k_i=1 α_iφ_i(t) + ε_t, то он представляет собой тренд.

Если ε_i(t) нелинейная ф-я, то тренд нелинейный, а если линейная, то линейный.

===========================================================

Билет№28

(1) Условная вер-ть. Теорема умнож-я вер-тей.

Произведением двух соб-й А и В наз. соб-е АВ, состоящее в совместном появлении этих соб-й ( А-деталь годная, В-деталь окрашенная, АВ- годная и окрашенная). Произ-ем неск. соб-й наз. соб-е состоящее в совместном появлении всех этих соб-й. Во введении случайное соб-е определено как соб-е, к-рое при осуществлении совок-ти условий S может произойти или не произойти. Если при вы­числении в-ти соб-я никаких др. ограничений, кроме условий S, не налагается, то такую в-ть наз. безусловной; если же налагаются и др. дополнительные условия, то в-ть соб-я наз. условной. Напр, часто вычисляют в-ть собы-я В при дополнительном условии, что произошло соб-е А. Заметим, что и безусловная в-ть, строго говоря, явл. условной, поскольку предполагается осуществление условий S.Условной в-тью Ра(В) наз. в-ть соб-я В, вычисленную в Предположении, что соб-е А наступило: Ра(в)=Р(АВ)/Р(А) (Р(А)>0). Рассм-м два соб-я А и В, пусть вер-ти Р(А) и Ра(В) известны. Как найти совмещение этих соб-й,т.е. вер-ть того что появится и соб-е А и соб-е В. Ответ на этот вопрос дает теорема умнож-я: вер-ть совместного появл-я двух соб-й равна произведению в-ти одного из них на условную вер-ть другого, вычисленную в предположении, что первое соб-е уже наступило Р(АВ)=Р(А)*Ра(В). Д-во : по определению условной вер-ти Ра(В)=Р(АВ)/Р(А), отсюда Р(АВ)=Р(А)*Ра(В). Следствие: вер-ть совместного появл-я неск. соб-й равна произведению в-ти одного из них на условные в-ти всех остальных, причем вер-ть каждого последующего соб-я вычисляется в предположении, что все предыдущие соб-я уже появились

Где______________________ вер-ть соб-я ______. Вычисленная в предположении, что соб-я ___________________ наступили. В частности, для трех соб-й___________________________________ (порядок может быть выбран любой, безразлично какое соб-е считать перв., вторым).

==========================================================

Билет№23

(1) Ф-я Лапласа, ее св-ва. Вер-ть попадания в интервал для норм. распред-я с.в. Правило 3 сигм. Если случ. Вел-на Х задана плот-тью распред-я ____, то вер-ть того, что Х примет знач-е, принадлежащее интервалу ________, такова:

Пусть случ. Вел-на Х распределена по нормальному закону. Тогда вер-ть того, что Х примет знач-е, принадлежащее интервалу __________, равна

Преобразуем эту ф-лу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную _____________. Отсюда ______________________________. Найдем новые пределы интегрирования. Если ______, то ____________; если ______ то_____________. Таким образом, имеем

Пользуясь ф-цией Лапласа (Теорема: раз в-ть того, что в n независ. исп-ях в кажд. из к-рых в-ть появл-я соб-я А равно р, причем 1>р>0, то соб-е А наступит не менее m₁ раз и не более m₂ раза приблизительно равно

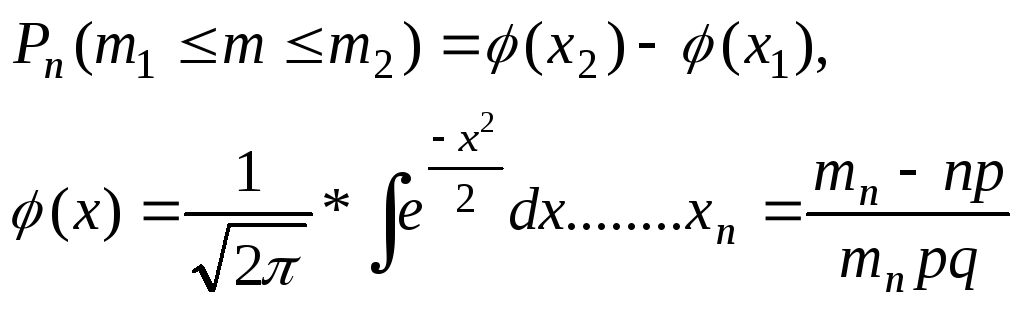
При решении задач, требующих применения инт. Теоремы, пользуются спец. Таблицами, так как неопред. интеграл ___________ не выражается ч-з элементарные ф-ции. В ней даны знач-я ф-ции _______ для положит. Знач-й х и для х=0, для х<0 пользуются той же табл.й (т.к. ф-я ______ нечетка). Ф-цию _______ часто наз. Ф-ей Лапласа. Вер-ть того, что соб-е А появится в n исп-ях от к1 до к2 раз:

Окончательно получим

Правило 3-х сигм: преобразуем ф-лу

Положив ____________. В итоге получим

Если _________ и , =>, _____________, то

Т.е. вер-ть того, что отклонение по абсолютной вел-не будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Др. словами, в-ть того, что абсолютная вел-на отклонения превысит утроенное ср. квадратическое отклонение, оч. мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие соб-я исходя из принципа невозмож­ности маловероятных соб-й можно считать практически невозм.. В этом и состоит сущность правила трех сигм: если случ. вел-на распределена нормально, то абсолютная вел-на ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квад-ратического отклонения.На практике правило трех сигм применяют так: если распред-е изучаемой случ. вел-ны неизвестно, но условие, указанное в приведенном правиле, выпол­няется, то есть основание предполагать, что изучаемая вел-на распределена нормально; в противном случае она не распределена нормально.

F(х;у).

(2) Двумерная ф-я распред-я и ее св-ва. (стр. 158 +гр-к)Рассм-м двумерную случ. Вел-ну (Х: У) (безразлично, дискрутную или непрерывную). Пусть х, у – пара действительных чисел. Вер-ть соб-я, состоящего в том, что Х примет знач-е, меньшее х, и при этом У примет знач-е, меньшее у, обозначим ч-з F(х;у). Если х и у будут изменяться, то, вообще говоря, будет изменяться и F(х;у), т.е. F(х;у) есть ф-я от х и у. Ф-цией распред-я двумерной случ. вел-ны (Х; У) наз. ф-цию F(х;у), определяющую для каждой пары чисел х, у вер-ть того, что Х примет знач-е, меньшее х, и при этом У примет знач-е, меньшее у: F(х;у)=Р (Х< х, У <у). Геом-ки это рав-во можно истолковать так: F(х;у) есть вер-ть того, что случ. точка (Х; У) попадет в бесконечный квадрант с вершиной (х,у), расположенный левее и ниже этой вершины. Св-во1:знач-е ф-и распред-я удовлетворяют двойному нер-ву ______________________. Д-во: св-во вытекает из опред-я ф-ции распред-я как вер-ти: вер-ть – всегда неотрицат. Число. Не превышающее единицу. Св-во2: F(х;у) есть неубывающая ф-я по кажд.у аргументу, т.е.

Св-во3: имеют место предельные соотн-ниея

Св-во4: а) при у=_____ ф-я распред-я системы становится ф-цией распред-я составляющей Х:_____________________. Б) при х=_____ ф-я распред-я системы становится ф-ей распред-я составляющей У:

_______________________.

============================================================

Билет№ 24

(1)Нерав-во Чебышева. (стр. 102)

Нерав-во Ч. справедливо для дискр. И непрер. случ. Вел-н. Рассм-м диск. Случ. В-ну Х. Заданную табл.й распред-я:

Поставим перед собой задачу оценить вер-ть того, что отклонение случ. Вел-ны от ее МО не превышает по абсолютной вел-не полож. Числа _____. Если _____ достаточно мало, то мы оценим. Таким образом, вер-ть того, что Х примет знач-я, достаточно близкие к своему мат. Ожиданию. Ч. доказал нерав-во, позволяющее дать интересующую нас оценку. Неравен-во Ч.: вер-ть того, чт отклонение случ. Вел-ны Х от ее МО по абсолютной вел-не меньше полож. Числа _____, не меньше чем _____________________:

Д-во: так как соб-я, состоящие в осуществлении неравенств ____________________________, противоположны, то сумма их в-тей равна ед-це, т.е.

Отсюда интересующая нас вер-ть

Т.о., задача сводится к вычислению вер-ти __________________________. Напишем выражение дисперсии случ. Вел-ны Х:

Очевидно, все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у к-рых ___________________________(для оставшихся слагаемых ___________________________), вследствие чего сумма может только уменьшиться. Условимся считать для опред.сти, что отброшено k перв. слагаемых ( не нарушая общности, можно считать, что в табл. распред-я возм. знач-я занумерованы именно в таком порядке). Таким образом,

Заметим, что обе части нерав-ва ______________________________________________ положительны, поэтому. Возведя их в квадрат, получим равносильное нерав-во _________________________. Воспользуемся этим замечанием и, заменяя в оставшейся сумме каждый из множителей___________________ числом _________ ( при этом нерав-во может лишь усилиться), получим

По теореме слож-я, сумма вер-тей ________________________ есть вер-ть того, что Х примет одно, безразлично какое, из знач-й __________________________, а при любом из них отклонение удовлетворяет нер-ву ________________________. Отсюда следует, что сумма ______________________ выражает вер-ть

Это соображение позволяет переписать нерав-во (**) так:

Или

Подставляя (***) в (*), окончательно получим

ч.т.д.