5.4. Электропроводность полупроводников

Электропроводностьпредставляет собой явление, связанное с переносом свободных носителей заряда под действием электрического поля.

Полупроводники высокой степени очистки в области не слишком высоких температур обладают электропроводностью собственных носителей заряда – электронов и дырок. Такую электропроводность называют собственной. Собственнаяудельнаяэлектропроводность пропорциональна концентрации и подвижности носителей заряда

σ=е(n_iµ_n+p_iµ_p). (5.55)

Подставляя в последнее выражение n_iиp_iиз (5.41) иµ_nиµ_pиз (5.23) получим

σ_i=σ₀exp(-E_g/2kT), (5.56)

где σ₀– множитель, практически не зависящий от температуры.

Температурную зависимость (5.56) удобно представить в полулогарифмических координатах

. (5.57)

График (5.57) представляет собой прямую линию, отсекающую на оси ординат отрезок lnσ₀(рис. 5.6,а). Тангенс угла наклона данного графика представляет собой величинуE_g/2k

tgα_i=E_g/2k.

Таким образом, анализируя график (5.57), можно определить величины σ₀иE_g, что часто и применяется на практике. Также на практике часто используют прием полулогарифмических координат, чтобы выяснить наличие экспоненциальных функций в результатах эксперимента.

а)б)

Рис. 5.6. Температурная зависимость электропроводности полупроводника: а – собственный полупроводник;б– примесный полупроводник

Температурная зависимость электропроводности невырожденных примесных полупроводников, как и для собственных полупроводников, в основном определяется температурной зависимостью концентрации носителей заряда.

На рис. 5.6, бсхематически показаны графики зависимостиσ(Т) в полулогарифмических координатах для полупроводника, содержащего различные концентрации примеси. На графиках можно выделить три области:ab,bc,cd.

Область abсоответствует низким температурам и ограничивается температурой истощения примеси (точкаb). С учетом концентрации и подвижности носителей можно записать выражение дляпримесной удельнойэлектропроводности

σ_n = σ_n0exp(-ΔE/2kT).(5.58)

Логарифмируя (5.58), получим выражение для областей ab

. (5.59)

Области bc– области истощения примеси, где все примесные атомы ионизированы, но энергия фононов недостаточна для перехода электронов из валентной зоны в зону проводимости.

Необходимо отметить, что участки bcсоответствуютуменьшению электропроводностиза счетсниженияподвижности носителей заряда. С ростом концентрации примеси эти участки уменьшаются и в случаеN=N_Зучастокbcисчезает. Примесная проводимость непосредственно переходит в собственную.

Рассмотренные результаты относились к моноатомнымполупроводникам. Всложныхполупроводниках, например, типаA^IIIB^V, зависимости подвижности и электропроводности от температуры выглядят несколько иначе. Рассмотрение этого вопроса выходит за рамки данного пособия и может быть найдено, например, в [10].

5.5. Электропроводность металлов и сплавов

В металлах концентрация электронного газа максимальнаи поэтому практическинезависит от температуры. Вследствие этого температурная зависимость электропроводности металлов определяется температурной зависимостью подвижности электронов вырожденного электронного газа (п.5.2). В достаточно чистом металле, где концентрация примесей невелика, подвижность, вплоть до весьма низких температур, определяетсяэлектрон-фононным рассеянием.

Подставив (5.24) в выражение (5.15), получим зависимость

σ~ 1/Т, (5.60)

или для удельного сопротивления

ρ= 1/σ=αТ, (5.61)

где α– температурный коэффициент сопротивления.

В области низких температур концентрация фононного газа пропорциональнаТ³, поэтому длина свободного пробега

λ~Т^-3, (5.62)

а средний импульс фононов оказывается гораздо меньше импульса электрона.

В итоге эффективная длина свободного пробега электрона оказывается в сто раз меньше, а уточненные зависимости для ρиσпримут вид

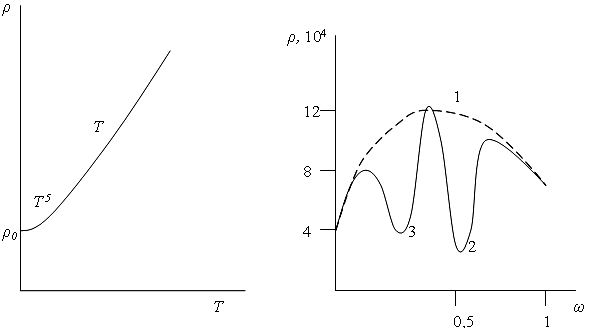
σ~Т ^-5,ρ~Т ⁵. (5.63)

В области температур, близких к абсолютному нулю, необходимо учитывать рассеяние электронов на примесных атомах. В этом случае, согласно (5.23), подвижность электронов не зависит от температуры и называется остаточным сопротивлениемρ₀

ρ=ρ_Т+ρ₀, (5.64)

где ρ_Т– доля температурнозависимого удельного сопротивления.

Последнее выражение называют правилом Матиссена, его график представлен на рис. 5.7, а.

~

~

а)б)

Рис. 5.7. Удельное сопротивление: а– металлы;б– сплавы;

1 – неотожженный состав; 2 – CuAu; 3 –Cu₃Au

Картина удельного сопротивления для сплавовоказывается гораздо более сложной, чем для чистых металлов. Она определяется химическим взаимодействием между компонентами сплава. Если химическое взаимодействие компонентов отсутствует, то примесные атомы создают дополнительные центры рассеяния электронов, искажая кристаллическую решетку металла. В этом случае удельное сопротивление сплава значительно выше, чем у чистых металлов. Для удельного сопротивления бинарных сплавов можно привести соотношение Нордгейма

ρ_спл=β[ω(1-ω)], (5.65)

где β– коэффициент пропорциональности;

ω, 1-ω– доли металлов, образующих сплав.

Очевидно, что ρ_сплимеет максимум приω= ½ (рис. 5.7,б, график 1).

Однако, если атомы сплавов могут вступать в реакцию и образовывать интерметаллические соединения, то появляются области с пониженным удельным сопротивлением (рис. 5.7,б, 2, 3). Данный эффект объясняется упорядочением структуры сплава в этих областях и, как следствие, возрастанием длины свободного пробега электрона.