2.4. Электрон в потенциальной яме

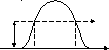
Рассмотрим движение микрочастицы энергии Eв прямоугольной потенциальной яме (рис. 2.2) глубинойU₀и ширинойL.

U w

U₀ E II

I III

0 L x 0 L x

a)б)

Рис. 2.2. Частица в потенциальной яме: а– энергетическая диаграмма;б– вероятность нахождения частицы

Для электрона примером такой ямы является микроэлектрод: вне электрода энергия электрона равняется нулю, а внутри – U₀. Эта энергия обеспечивается потенциальным полем решеткиU₀. Для выхода электрона из металла необходимо совершить работу, равнуюU₀–работу выхода.

Запишем стационарное уравнение Шредингера для областей I,II, иIII(рис. 2.2,а).

, (2.28)

где ,

.

Запишем общее решение уравнения Шредингера для трех зон.

, (2.29)

Упростим задачу, считая, что U₀∞. Тогда в областяхIиIIIволновая функция будет равна нулю.

Согласно условию непрерывности функции можно записать, что

ψ(0)=ψ(L)=0. (2.30)

Это условие выполнимо, если

kL =πn,n = 1, 2, …

Отсюда находим возможные значения k_n

. (2.31)

Поскольку стенки ямы имеют одинаковую высоту, очевидно, что в (2.29) A=B. Тогда можно записать выражение для волновой функции электрона в яме

или

(2.32)

В потенциальной яме укладывается целое число полуволн (рис. 2.2, б). Определим вероятность нахождения электрона в потенциальной яме ω(x).

где А– коэффициент, определяемый из условия нормировки,.

Тогда можно записать

(2.33)

Из данного выражения следует, что в отличие от свободного электрона вероятность нахождения электрона в потенциальной яме непостоянна и изменяется с изменением квантового числа n(рис. 2.2,б).

Вернемся к выражению (2.28) и запишем выражение для энергии электрона в яме.

.

Полученное выражение не отличается от записанного ранее (2.22) для свободного электрона. Однако, подставив в него kиз (2.31), получим новое выражение

. (2.34)

Полученное выражение содержит квантовое число n, т.е. спектр энергии электрона в потенциальной яме является несплошным, как для свободного электрона, адискретным.

2.5. Туннелирование микрочастиц сквозь потенциальный барьер

Эта задача возникла при исследовании радиоактивности. Выяснилось, что из ядер вылетают α-частицы, которые не имеют права на существование, т.к. их энергия меньше потенциального барьера ядра. Этому явлению Г. Гамовым было дано название туннельный эффект. В то время объяснить данный эффект не представлялось возможным. Это было сделано позднее, когда появился математический аппарат квантовой механики.

Пусть микрочастица падает на потенциальный барьер, двигаясь по оси x. Для простоты выбрана прямоугольная форма барьера (рис. 2.3).

U

U₀

E

I Е II III

x₁ x₂ x 0 d x

а)б)

Рис. 2.3. Потенциальный барьер: а– произвольной формы;б– прямоугольная

модель барьера

Запишем стационарное уравнение Шредингера (2.14).

.

Напомним, что решение данного уравнения для различных областей будет иметь вид

, (2.35)

, (2.36)

, (2.37)

где , (2.38)

. (2.39)

В формулах (2.35), (2.36), (2.37) первое слагаемое описывает падающую волну, а второе – отраженную от правой или левой стенок барьера. Естественно, что второе слагаемое в (2.37) равно нулю. Необходимо обратить внимание на то, что значение k₂– мнимая величина. Это говорит о том, что существование микрочастицы внутри барьера запрещено.

Вероятность туннельного прохождения барьера называют прозрачностью D, которая будет определяться отношением

, (2.40)

или выражением

, (2.41)

где D₀– коэффициент пропорциональности по порядку величины близкий к единице.

В табл. 2.1 приводится величина Dдля барьеров, имеющих одинаковую высотуU₀-E= 5 эВ, но разные толщины.

Таблица 2.1