
- •1.1. Основные этапы решения задач с помощью эвм
- •1.2. Погрешности результатов численного решения задач
- •1.3. Основные требования к алгоритмам и программному обеспечению
- •2.1. Метод дихотомии (деления отрезка пополам)
- •2.2. Метод хорд
- •2.3. Метод простой итерации
- •2.4. Метод Ньютона
- •2.5. Модификации метода Ньютона
- •3.1. Основные понятия вычислительной линейной алгебры
- •3.2. Некоторые точные методы решения слау
- •3.3. Итерационные методы решения слау
- •3.4. Вычисление собственных значений матрицы
- •4.1. Постановка задачи интерполяции
- •4.2. Полиномиальная интерполяция. Формула Лагранжа
- •4.3. Разделенные разности и интерполяционная формула Ньютона
- •4.4. Кусочно-полиномиальная интерполяция
- •4.4. Программы решения задач интерполяции с помощью Matlab
- •5.1. Численное дифференцирование
- •5.2. Погрешности методов численного дифференцирования
- •5.3. Численное интегрирование. Простейшие методы
- •5.4. Метод Ньютона-Котеса и его модификация
- •5.5. Методы Монте-Карло
- •6.1. Решение пере- и недоопределенных слау
- •6.2. Примеры решение переопределенной слау методом наименьших квадратов Пусть
- •6.3. Метод наименьших квадратов для регрессионного анализа
- •Задание к главе 6
- •7.1. Методы решения задачи Коши
- •7.2. Методы Рунге-Кутта решения задачи Коши
- •7.3. Решение краевой задачи для оду
- •Задания к главе 7
- •8.1. Решения дифференциальных уравнений первого порядка
- •8.2. Решения дифференциальных уравнений параболического типа
- •8.3. Решение дифференциальных уравнений эллиптического типа
- •8.4. Решение дифференциальных уравнений гиперболического типа
3.1. Основные понятия вычислительной линейной алгебры
Для
решения СЛАУ и других указанных задач
необходимо ввести ряд понятий. Если
![]() – приближенное решение системы (3.1), то
вектор
– приближенное решение системы (3.1), то
вектор![]() называетсяпогрешностью
решения
системы уравнений. Часто погрешности
решения системы уравнений оценивают
по вектору
называетсяпогрешностью
решения
системы уравнений. Часто погрешности
решения системы уравнений оценивают
по вектору
![]() ,
называемомуневязкой.
Вектор
,
называемомуневязкой.
Вектор
![]() показывает, насколько правая часть
системы отличается от левой, если
подставить в нее приближенное решение.
Очевидно, что и погрешность, и невязка
решения должны быть как можно меньше,
при этом они связаны очевидным равенством
показывает, насколько правая часть
системы отличается от левой, если
подставить в нее приближенное решение.
Очевидно, что и погрешность, и невязка
решения должны быть как можно меньше,
при этом они связаны очевидным равенством
![]() .
.
Величины погрешностей и невязок оцениваются при помощи нормы векторов и матриц.
Нормой
вектора
![]() называется вещественное число
называется вещественное число![]() ,
обладающее следующими свойствами:
,
обладающее следующими свойствами:
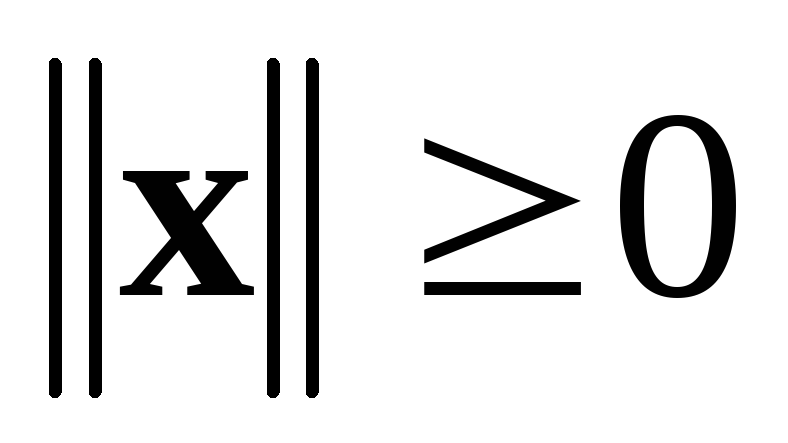 ,
причем
,
причем
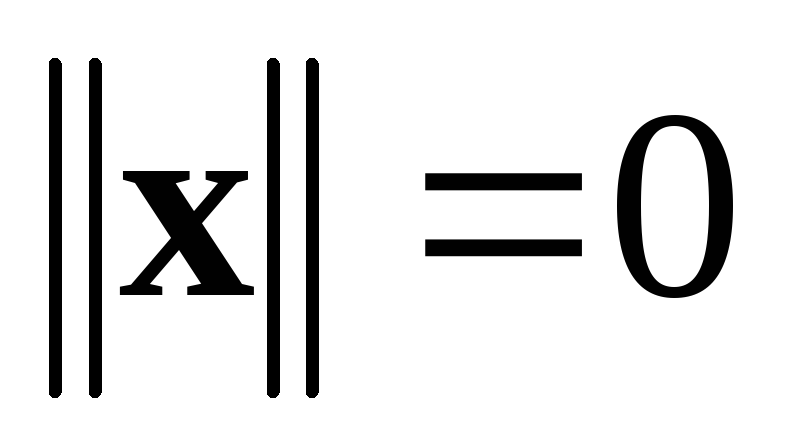 тогда и только тогда, когда
тогда и только тогда, когда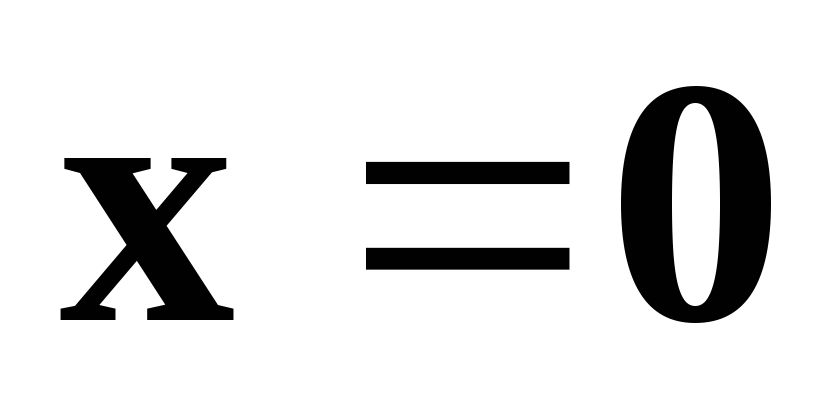 ;
;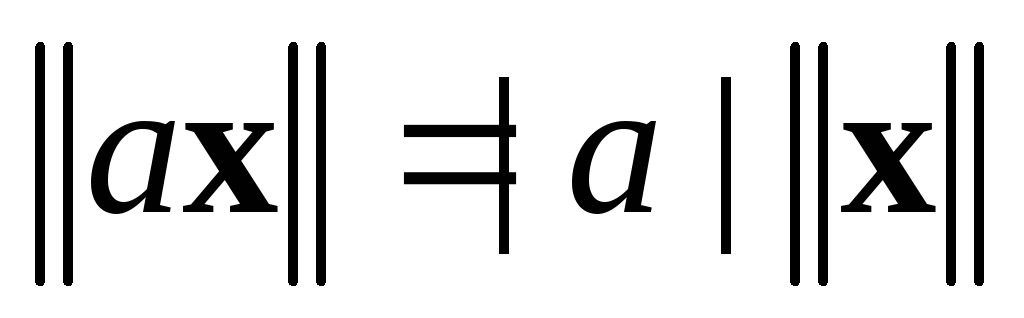 для
любого вектора
для
любого вектора
 и любого числа
и любого числа ;
;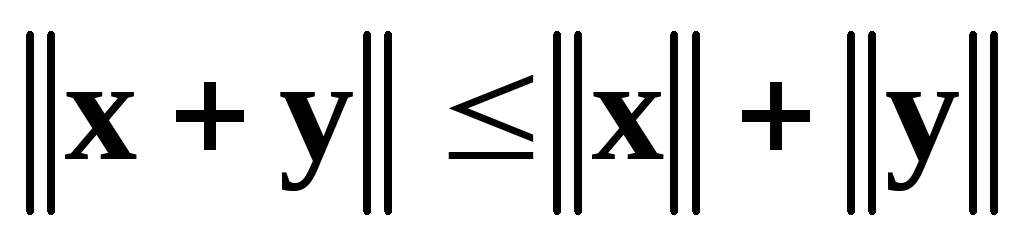 для
любых векторов
для
любых векторов
 и
и (неравенство треугольника).
(неравенство треугольника).
Существует множество способов введения норм, однако в вычислительных методах наиболее употребительны следующие три:
![]() ,
, 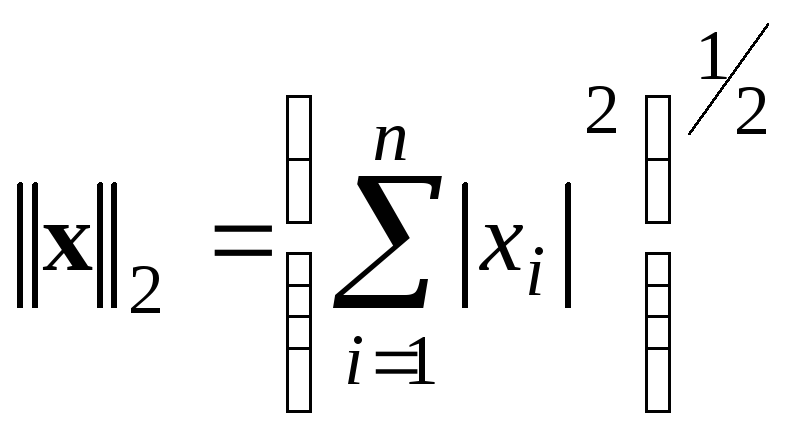 и
и![]() ,
,
которые являются частными случаями нормы общего вида
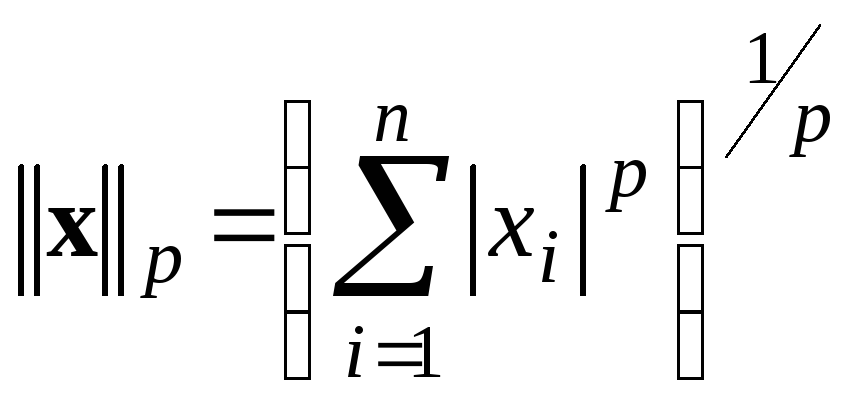 для
для
![]() .
.
Норму
![]() (при
(при![]() )
обычно называют евклидовой, норма
)
обычно называют евклидовой, норма![]() получается при
получается при![]() .
.
Скалярным
произведением
векторов
![]() и
и![]() называется величина
называется величина
![]() .
.
Нетрудно
установить, что
![]() .
.
Абсолютные
и относительные погрешности
вектора
![]() можно ввести как некоторую меру близости
векторов
можно ввести как некоторую меру близости
векторов![]() и
и![]() в виде нормы
в виде нормы![]() .
Отсюда абсолютная погрешность имеет
вид
.
Отсюда абсолютная погрешность имеет
вид
![]() ,
,
а относительная –
![]() ,
,
Выбор
той или иной нормы в практических задачах
диктуется требованиями, предъявляемыми
к точности решения. Выбор
![]() отвечает случаю, когда малой должна
быть суммарная абсолютная ошибка в
компонентах решения; выбор
отвечает случаю, когда малой должна
быть суммарная абсолютная ошибка в
компонентах решения; выбор![]() соответствует малости среднеквадратичной
ошибки, а выбор
соответствует малости среднеквадратичной
ошибки, а выбор![]() означает, что малой должна быть
максимальная из абсолютных ошибок в
компонентах решения.
означает, что малой должна быть
максимальная из абсолютных ошибок в
компонентах решения.
При
решении СЛАУ критерием сходимости
решения выбирают критерий сходимости
по норме. Пусть
![]() – последовательность векторов
– последовательность векторов![]() .
Она сходится к вектору
.
Она сходится к вектору![]() при
при![]() (
(![]() ),
если
),
если![]() при
при![]() (
(![]() ).
Отметим, что наличие или отсутствие
сходимости не зависит от вида выбранной
нормы и последовательность
).
Отметим, что наличие или отсутствие
сходимости не зависит от вида выбранной
нормы и последовательность![]() сходится к вектору
сходится к вектору![]() при
при![]() тогда и только тогда, когда для всех
тогда и только тогда, когда для всех![]() имеем
имеем![]() при
при![]() ,
т.е. сходимость по норме эквивалентна
покоординатной сходимости.
,
т.е. сходимость по норме эквивалентна
покоординатной сходимости.
Норма
матрицы
![]() ,
подчиненная норме векторов
,
подчиненная норме векторов![]() ,
определяется величиной
,
определяется величиной
![]() .
.
Норма матрицы обладает теми же свойствами, что и норма вектора:
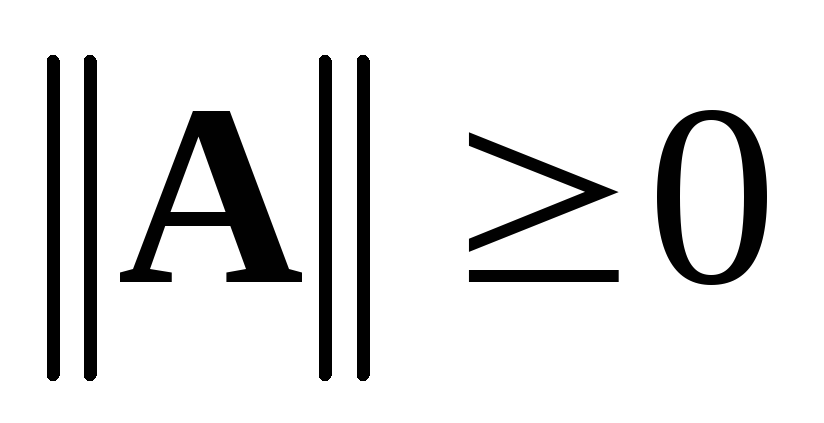 ,
причем
,
причем
 тогда и только тогда, когда
тогда и только тогда, когда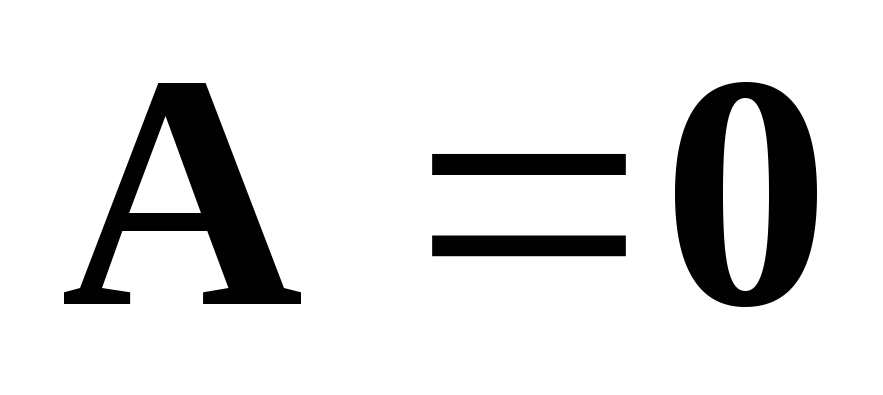 ;
;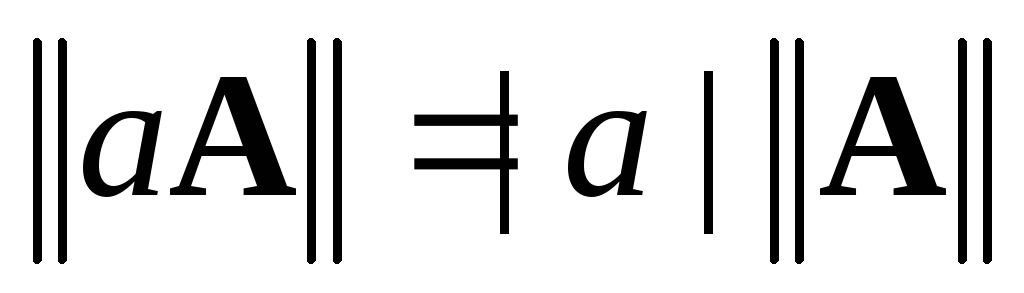 для
любой матрицы
для
любой матрицы
 и любого числа
и любого числа ;
;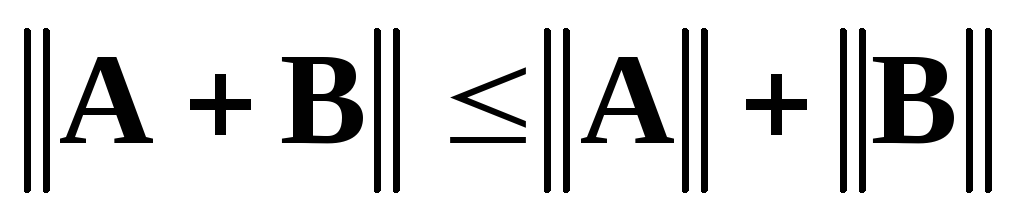 для
любых матриц
для
любых матриц
 и
и ,
,
дополнительно к этому верны следующие свойства:
 для
любых матриц
для
любых матриц
 и
и ,
которые можно умножать;
,
которые можно умножать;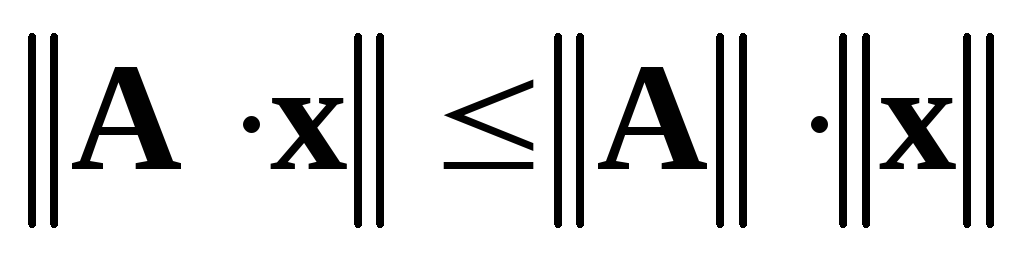 для
любой матрицы
для
любой матрицы
 и любого вектора
и любого вектора .
.
Как
следует из определения (3.9), каждой из
векторных норм
![]() соответствует своя подчиненная норма
соответствует своя подчиненная норма![]() .
В частности, нормам
.
В частности, нормам![]() ,
,![]() и
и![]() соответствуют нормы
соответствуют нормы![]() ,
,![]() и
и![]() ,
определяемые по формулам
,
определяемые по формулам
![]() ,
,
![]() ,
,
![]() – собственные числа матрицы
– собственные числа матрицы![]() ,
,
![]() .
.
Таким
образом, для получения первой нормы
необходимо найти сумму модулей элементов
каждого из столбцов матрицы
![]() ,
а затем выбрать максимальную из этих
сумм. Для получения нормы
,
а затем выбрать максимальную из этих
сумм. Для получения нормы![]() аналогичным образом следует поступить
со строками матрицы.
аналогичным образом следует поступить
со строками матрицы.
Очень
часто в приложениях СЛАУ определена
приближенно, т.е. имеются некоторые
малые возмущения коэффициентов
![]() и коэффициентов
и коэффициентов![]() .
Рассмотрим возмущенную систему
.
Рассмотрим возмущенную систему![]() и обозначим
и обозначим![]() ,
,![]() ,
,![]() .
Если матрица
.
Если матрица![]() имеет обратную и выполнено условие
имеет обратную и выполнено условие
![]() ,
,
то
матрица
![]() имеет обратную и справедлива оценка
относительной погрешности решения
имеет обратную и справедлива оценка
относительной погрешности решения
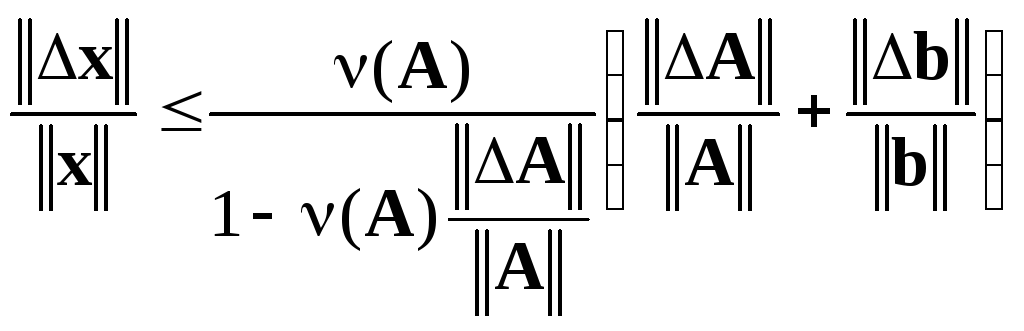 , (3.3)
, (3.3)
где
![]()
представляет
собой число обусловленности матрицы
![]() ,
характеризующее при
,
характеризующее при![]() степень зависимости относительной
погрешности решения от относительной
погрешности правой части. Если матрица
степень зависимости относительной
погрешности решения от относительной
погрешности правой части. Если матрица![]() близка к вырожденной, то число
близка к вырожденной, то число![]() будет велико, и в этом случае матрица
будет велико, и в этом случае матрица![]() плохо обусловлена.
плохо обусловлена.
Эффективность вычислений в линейной алгебре существенно зависит от умения использовать структуру и свойства матриц. Некоторые важные типы матриц приведены ниже.
Квадратная
матрица
![]() называетсядиагональной,
если элементы
называетсядиагональной,
если элементы
![]() при
при![]() ,
а элементы, отличные от нуля, располагаются
на главной диагонали. Диагональную
матрицу, у которой все элементы главной
диагонали равны единице, называютединичной
и обозначают
,
а элементы, отличные от нуля, располагаются
на главной диагонали. Диагональную
матрицу, у которой все элементы главной
диагонали равны единице, называютединичной
и обозначают
![]() :
:
 ,
,  .
.
Важную
роль в вычислительной линейной алгебре
играют треугольные
матрицы.
Квадратную матрицу
![]() называютнижней
треугольной,
если все ее элементы расположены ниже
главной диагонали (
называютнижней
треугольной,
если все ее элементы расположены ниже
главной диагонали (![]() для
для![]() ).
При равенстве нулю всех элементов
матрицы, расположенных выше главной
диагонали (
).
При равенстве нулю всех элементов
матрицы, расположенных выше главной
диагонали (![]() для
для![]() ),
матрицу называютверхней
треугольной.
Нижняя и верхняя треугольные матрицы
имеют соответственно следующий вид
),
матрицу называютверхней
треугольной.
Нижняя и верхняя треугольные матрицы
имеют соответственно следующий вид
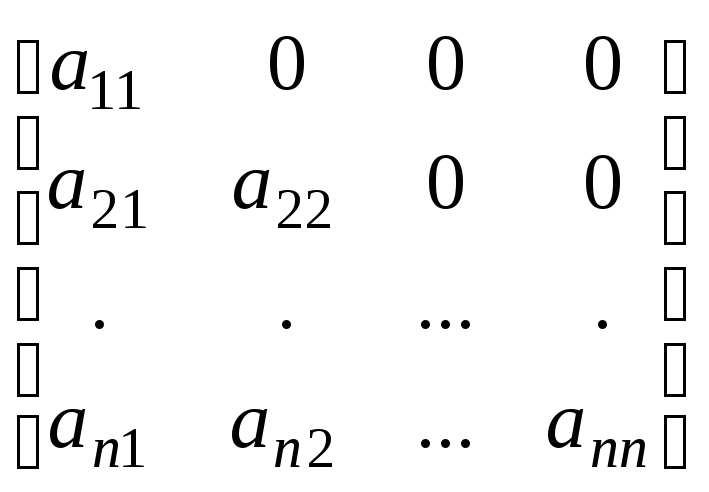 ,
,  .
.
Определитель треугольных матриц легко вычисляется по формуле
![]() .
.
Квадратная
матрица
![]() называетсясимметричной,
если она совпадает со своей транспонированной
матрицей
называетсясимметричной,
если она совпадает со своей транспонированной
матрицей
![]() ,
т.е.
,
т.е.![]() .
Очевидно, что диагональная и единичная
матрицы являются симметричными. При
этом значения квадратичной формы
положительно определенной симметричной
матрицы
.
Очевидно, что диагональная и единичная
матрицы являются симметричными. При
этом значения квадратичной формы
положительно определенной симметричной
матрицы![]() (
(![]() )
лежат в пределах
)
лежат в пределах
![]() ,
,
где
![]() и
и![]() – минимальное и максимальное собственные
значения матрицы.
– минимальное и максимальное собственные
значения матрицы.
Различные прикладные задачи часто приводят к матрицам, в которых число ненулевых элементов много меньше общего числа элементов матрицы, такие матрицы принято называть разреженными. Одним из источников таких матриц являются математические модели технических устройств, состоящих из элементов, связи между которыми локальны. Примером разреженной матрицы служит ленточная матрица, все ненулевые элементы которой расположены на ближайших к главной диагоналях. Простейшим представителем ленточной матрицы является трехдиагональная матрица
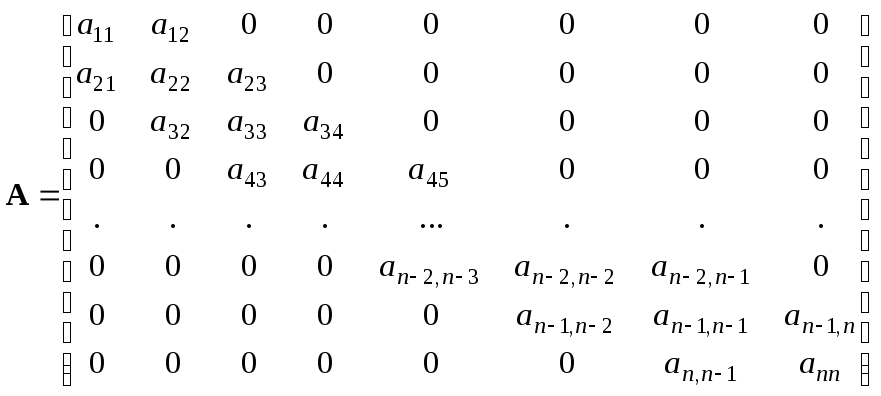 .
.
