8.2. Решения дифференциальных уравнений параболического типа

Рассмотрим уравнение теплопроводности, описывающее распространение тепла в однородном стержне

, (8.13)

где функция определяет температуру стержня в сечении в момент времени , , а . Здесь – коэффициент температуропроводности, – заданная функция, равная нулю, если внутри стержня отсутствуют источники тепла. Нетрудно убедится, используя канонический вид дифференциального уравнения (8.1) и выражение для вычисления дискриминанта (8.2), что это уравнение является дифференциальным уравнением параболического типа.

Построим разностную схему решения дифференциального уравнения (8.13) с начальным условием и граничными условиями

, . (8.14)

Как и раньше введем прямоугольную сетку, на которой определим и . Заменим производные и разностными отношениями, причем производную будем аппроксимировать в слое j, в результате получим разностную схему

, (8.15)

для . С начальными и граничными условиями

, (8.16)

при . Данной схеме соответствует следующий шаблон

|

——

Если же производную аппроксимировать разностным отношением не на слое j, а на слое (j+1), то получим разностную схему

. (8.17)

В этом случае с теми же начальными и граничными условиями, что и для схемы (8.15). Этой схеме соответствует шаблон

——

|

В схеме (8.15) в каждом уравнении содержится только одно значение функции на следующем слое. Это значение явно выражается через значения функции на данном слое, поэтому эта схема называется явной. Схема (8.17) содержит в каждом уравнении несколько неизвестных значений функции на новом слое, такая схема называется неявной. Перепишем схему (8.17) в следующем виде

, (8.18)

с граничными условиями

для . На каждом слое с номером схема (8.18) представляет собой систему линейных алгебраических уравнений для определения величин , правые части этих уравнений известны, поскольку содержат значения решения в предыдущем слое и значения известной функции .

Пусть , и . Тогда уравнения (8.18) преобразуются к виду

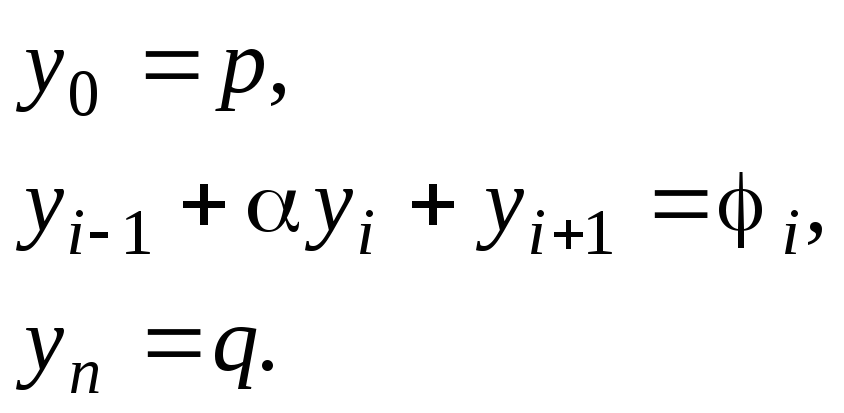при , (8.19)

Эта система линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов, она может быть решена методом прогонки.

Введем обозначения , , и рассмотрим однородное дифференциальное уравнение. Неявная схема будет представлена уравнениями:

(8.20)

при , а явная схема:

(8.21)

или

. (8.22)

Исследуем устойчивость схем вычисления с использованием принципа максимума. Внесем ошибку на исходном слое, тогда ошибка на новом слое будет удовлетворять для явной схемы равенству

,

из которого следует, что

.

Решая неравенство

,

получаем условие устойчивости явной схемы

. (8.23)

Для неявной схемы, аналогично рассуждая, получаем равенство

,

откуда следует, что неравенство

выполняется при всех . Это означает, что неявная схема является безусловно устойчивой.

Приведем фрагмент m-файла для нахождения решения по явной схеме (8.15). Температура на концах стержня считается постоянной. Предварительно должно быть задано начальное распределение температуры в стержне – вектор размерности . Вектор , также имеющей размерность , задает координаты точек стержня, в которых рассчитывается температура. Параметр определяет значение величины . Значения функции вычисляются до слоя , кроме того, запоминается распределение температур в слоях , , (). На графике показывается начальное распределение температуры, распределение температуры в промежуточных слоях и распределение температуры в последнем просчитанном слое с номером .

Программа 8.1

v=u;

u0=u;

for j=1:m4,

for i=2:(n-1),

v(i)=u(i)+s*(u(i-1)-2u(i)+u(i+1));

end

u=v;

if j==m1,

u1=u;

end

if j==m2,

u2=u;

end

if j==m3,

u3=u;

end,

end

u4=u;

plot(x,u0,x,u1,x,u2,x,u3,x,u4)