4.3. Разделенные разности и интерполяционная формула Ньютона

Для вычислений удобна форма записи интерполяционного полинома, связанная с разделенными разностями. Введем разделенные разности для известных точек :

• нулевого порядка ;

• первого порядка ;

• второго порядка 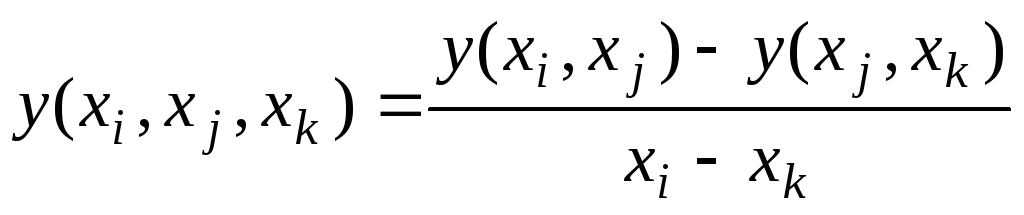и т.д.

Разделенные разности имеют размерности соответствующих производных функции . Если исходная функция представима в виде полиномастепени , то разделенные разности можно записать относительно этого полинома соответственно:

• первого порядка ;

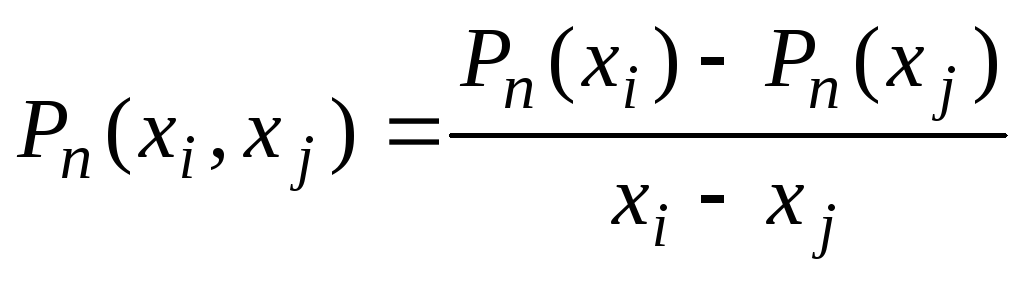• второго порядка и т.д.

Для разделенных разностей справедливо равенство

, (4.12)

доказательство которого можно провести по индукции.

Непосредственно из (4.12) вытекает ряд следствий:

1. Разделенная разность является линейным оператором относительно функции :

;

2. Разделенная разность есть симметрическая функция своих аргументов (т.е. не изменяется при любой их перестановке).

Если функция задана в точках , то таблицу

называют таблицей ее разделенных разностей.

Построим интерполяционные формулы, используя разделенные разности полиномов. Пусть – полином степени . Вычтя из константу , получим полином , который обращается в нуль при и поэтому делится нацело на . Следовательно, первая разделенная разность полинома степени

(4.13)

есть полином степени относительно и в силу симметричности выражения (4.13) относительно . Аналогично вторая разность есть полином степени. В самом деле, числитель разделенной разности

(4.14)

обращается в нуль при и, значит, нацело делится на , а степень полинома при этом уменьшается на единицу. Далее можно показать, что разделенная разность есть полином нулевой степени, т.е. константа, а разделенные разности более высоких порядков равны нулю.

Выразив из (4.13) полином , а из (4.14) полином получим

(4.15)

и т.д. Эта цепочка соотношений конечна, так как разделенная разность полинома равна нулю. Последовательно подставив эти соотношения друг в друга, получим формулу

которая содержит значения разделенных разностей полинома в узлах . Однако значения интерполяционного полинома в узлах по определению совпадают со значениями функции и поэтому разделенные разности функций и равны. Подставив в полученную формулу разделенные разности функции , получим интерполяционный полином в виде

. (4.16)

Этот полином называется интерполяционным полиномом Ньютона.

Пример. Пусть функция . Выберем в качестве узлов точки . Составим таблицу разделенных разностей:

0	0,000
		0,500
1	0,500		–0,067
		0,366		–0,016
2	0,866		–0,116
		0,134
3	1,000

С учетом найденных величин, получим

.

Применив интерполяционный полином, можно приближенно найти значения функции в точках, не совпадающих с узлами. В нашем случае, например, .

Если узлы интерполяции отстоят друг от друга на одном и том же расстоянии, т.е. удовлетворяют соотношению , где , а , то, обозначив , получим следующие равенства:

,

и т.д. В общем случае

, (4.17)

где . Тогда

Поэтому интерполяционный полином (4.16) преобразуется к виду

. (4.18)