Для экспоненциальных сигналов в качестве длительности сигнала обычно берется время, при котором амплитуда сигнала убывает в e 2.7... раз. Поэтому длительность экспоненциального сигнала равна
t a1
Будем определять эффективную ширину спектра по уровню 0.1 от максимума. Из графика видно, что эта ширина составляет примерно
10 a
Таким образом, база экспоненциального сигнала равна
t 10
! Найти аналитическое выражение АЧХ и ФЧХ экспоненциального сигнала 
33
Гауссов
импульс
s(t) exp( a2t2 )
Вычисляем спектр S( )с помощью прямого преобразования Фурье
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
||||||||||
S( ) |
e a |
t |
|
e i t d t |
exp |
|
|
|
|
|||||
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
a |
|
|
|
4 a |
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
||||
Поскольку сигнал является четной действительной функцией, его спектр получился чисто вещественной функцией, кроме того положительной функцией. Это означает, что амплитудно- частотная характеристика АЧХ совпадает со спектральной функцией. Фазово-частотная характеристика ФЧХ в этом случае
просто равна нулю.
( ) 0
34
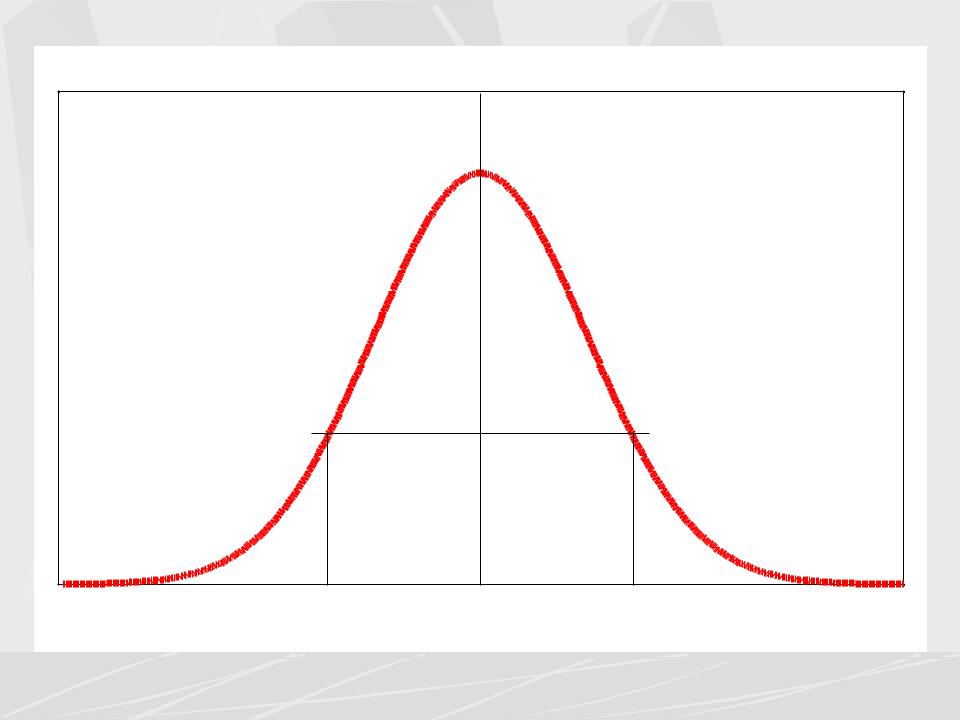
Gaussian pulse
|
s(t) |
|
|
|
1 |
|
|
|
1/e |
|
|
1/a |
0 |
1/a |
t |
|
|
|
35 |
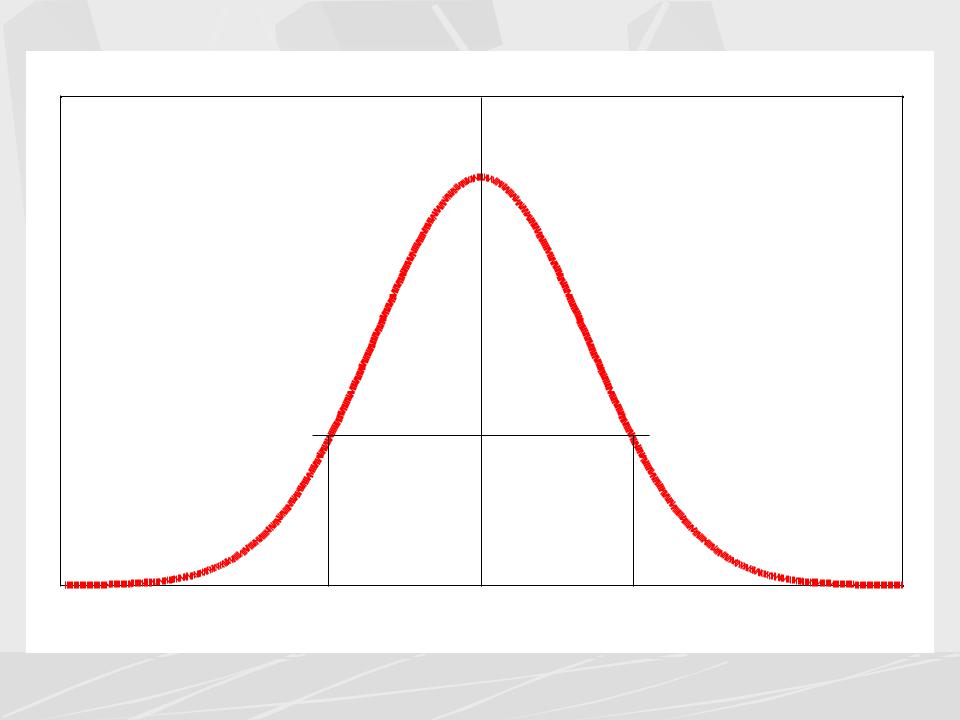
Gaussian pulse AFC
|
|
) |
|
|
A( |
|
|
1/2/a |
|
|
|
( 1/2/a)/e |
|
|
|
2a |
0 |
2a |
|
|
|
|
36 |
Важным свойством гауссова импульса является то, что его спектр также описывается гауссовой функцией.
Определим его эффективную длительность и ширину спектра
по уровню от максимума1/ e |
. Тогда получим |
|||
t |
2 |
, |
2 a |
|
a |
||||
|
|
|
||
База гауссова сигнала, таким образом, равна четырем
t 4
! Провести интегрирование прямого преобразования Фурье гауссово
сигнала
37
сновные понятия функционального анали
Линейное пространство
Линейное пространство (ЛП) – множество элементов E произвольной природы, для которых определены операции сложения и умножения на скаляр, удовлетворяющие следующим аксиомам:
A1. x, y E |
x y y x |
|
A2. x, y, z E |
(x y) z x ( y z) |
|
A3. |
x E, 0 E |
x 0 x |
A4. |
x E, , R |
( x ) ( ) x |
A5. |
x E, , R |
( ) x x x |
A6. |
x E, R |
( x y ) x y |
A7. x E |
0 x 0, 1 x x |
|
38
Линейное нормированное пространство
Линейное пространство называется линейным нормированным пространством (ЛНП), если каждому элементу , поставлено в соответствие число 
x 
.
Это число называется нормой элемента, и удовлетворяет следующим аксиомам (аксиомам нормы).
A1. x E |
|
|
|
|
|
|
x |
|
|
|
0, |
|
|
|
|
|
x |
|
|
|
|
|
|
|
0 x 0 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
A2. |
x E, R |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
A3. |
x, y E |
|
|
|
|
x y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
39
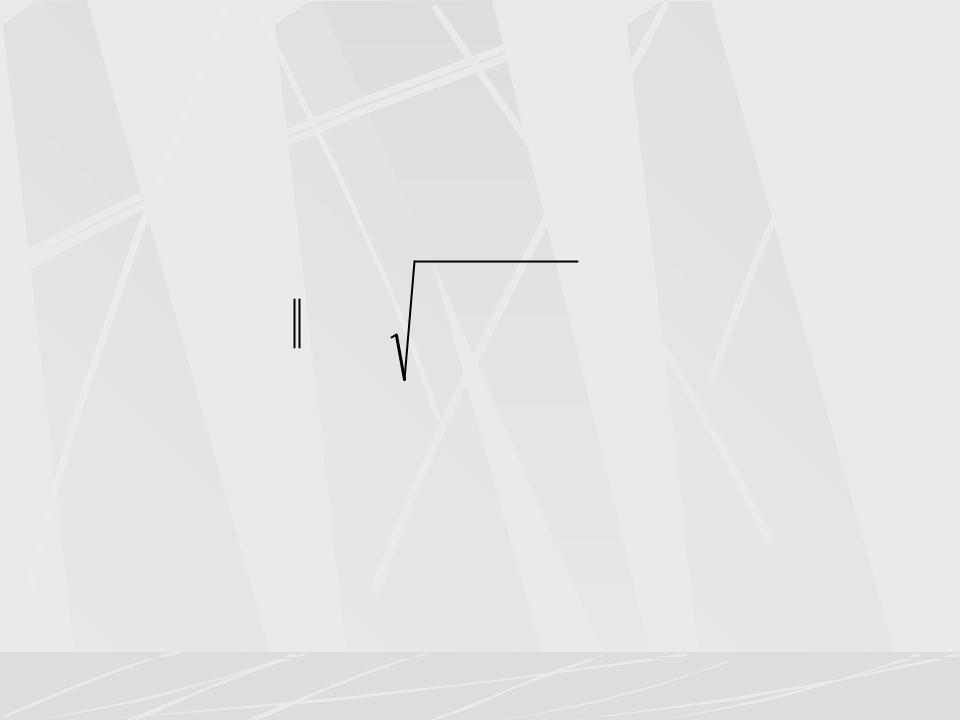
Энергия сигнала
Норму, которая удовлетворяет аксиомам нормы, можно определить разными способами. Для задач ЦОС наиболее подходит норма, определенная следующим образом:
|
|
|
|
|
|
s |
|
|
|
|
s2 (t) d t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Квадрат такой нормы будем называть энергией сигнала.
Es 
s 
2 s2 (t) d t
ЛНП с конечной нормой называется пространством функций с интегрируемым квадратом, и обозначается
L2 .
40
Метрика (расстояние)
ЛП называется метрическим пространством, если каждой паре элементов ( x, y ) поставлено в соответствие неотрицательное число ( x, y) , называемое метрикой (расстоянием), удовлетворяющее следующим аксиомам (аксиомам метрики).
A1. ( x, y) ( y, x) A2. ( x, y) 0 x y
A3. ( x, y) ( x, z) ( z, y)
Обычно метрику вводят следующим образом:
( x, y ) 
x y 
41
Скалярное
произведение
ЛП называется евклидовым, если каждой паре элементов ( x, y ) поставлено в соответствие вещественное число x, y , называемое скалярным произведением, удовлетворяющее следующим аксиомам:
A1. x, x 0, x, x 0 x 0
A2. x, y y, x
A3. x, y x, y
A4. x y, z x, z y, z
42