Продемонстрируем это на примере прямоугольного импульса. Рассмотрим сигнал следующего вида
s(t) sin ( t / T )
( t / T )
Вычисляем спектр S( ) с помощью прямого преобразования Фурье
|
T , |
|
|
|
/ T , |
|||
|
|
|||||||
|
|
|
|
|
|
|
|
|
S( ) s(t) e i t d t |
0, |
|
|
|
|
|
/ T |
|
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
Следующие рисунки показывают импульс и его спектр.
21
|
|
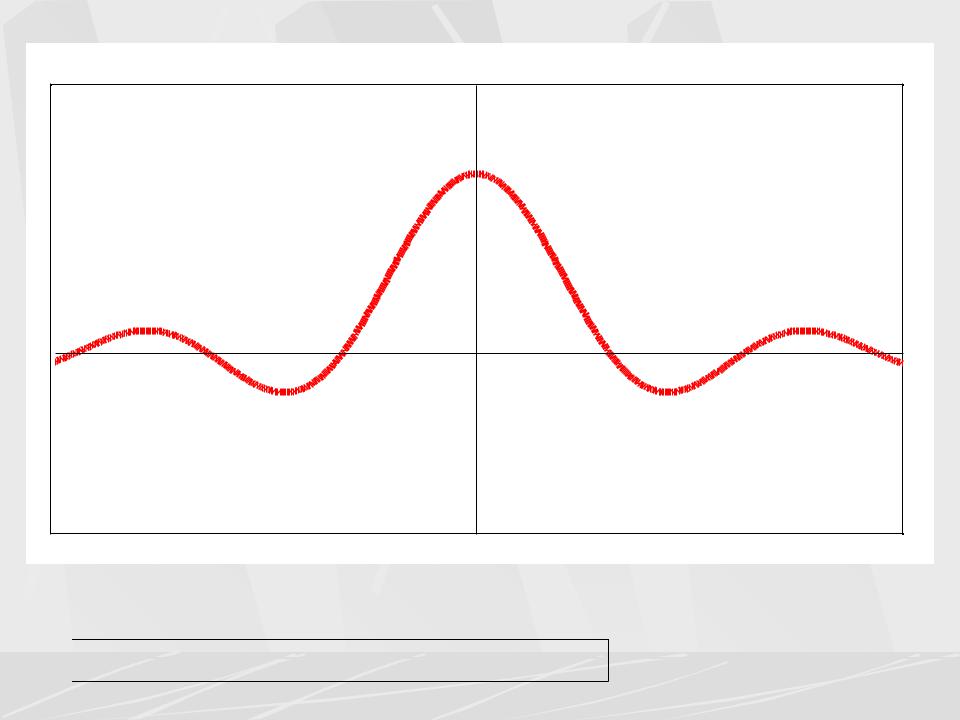
Signal |
|
|
|
|
|
s(t) |
|
|
|
|
|
1 |
|
|
|
2T |
T |
0 |
T |
2T |
t |
|
|||||
! Построить АЧХ и ФЧХ данного сигнала |
|
|
|||
22
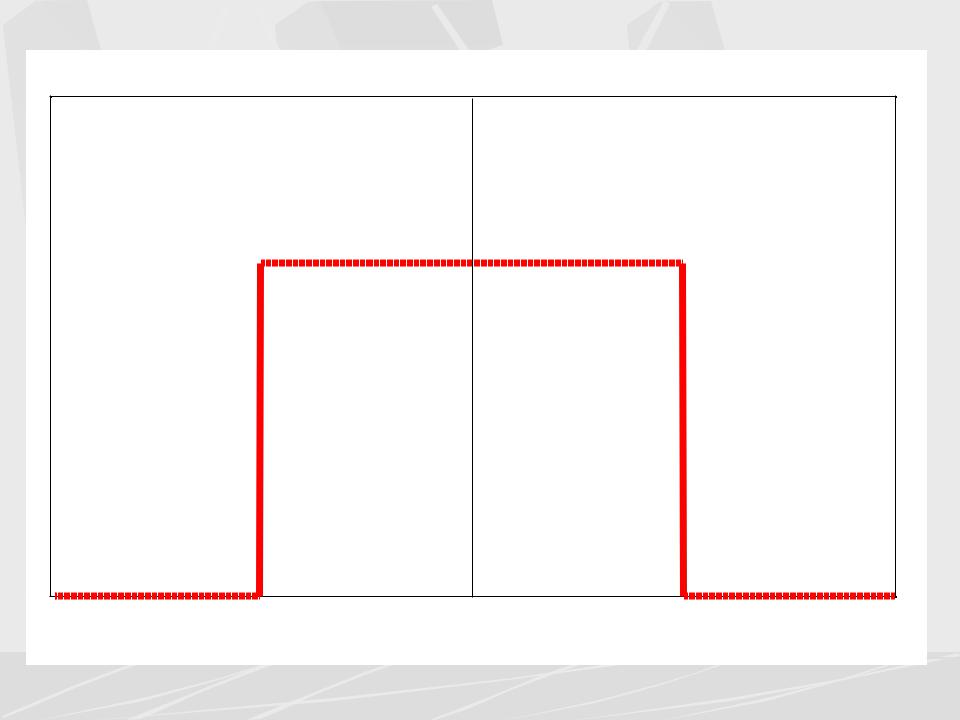
Signal spectrum
S( )
T
/T |
0 |
/T |
|
23
Несимметричный треугольный
импульс
Рассмотрим несимметричный треугольный импульс.
|
|
t |
, |
0 t T , |
|
|
|
||
|
|
|||
s(t) T |
|
|
||
|
0, |
|
t 0, t T |
|
|
|
|||
Вычисляем спектр S( ) с помощью прямого преобразования Фурье
T |
|
|
1 |
|
|
1 |
|
S( ) t |
e i t d t |
|
1 e i T |
e i T |
|||
2 |
T |
i |
|||||
0 |
T |
|
(i ) |
|
|
||
Следующие рисунки показывают несимметричный треугольный
импульс и его АЧХ и ФЧХ
24
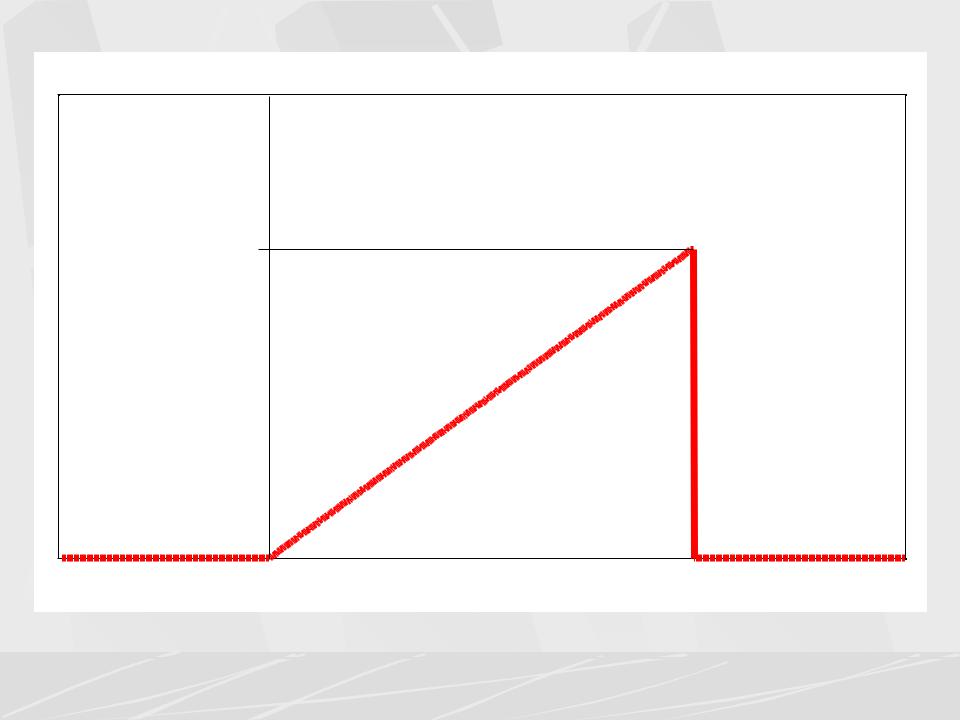
Triangular pulse
s(t) |
|
|
1 |
|
|
0 |
T |
t |
|
|
25 |
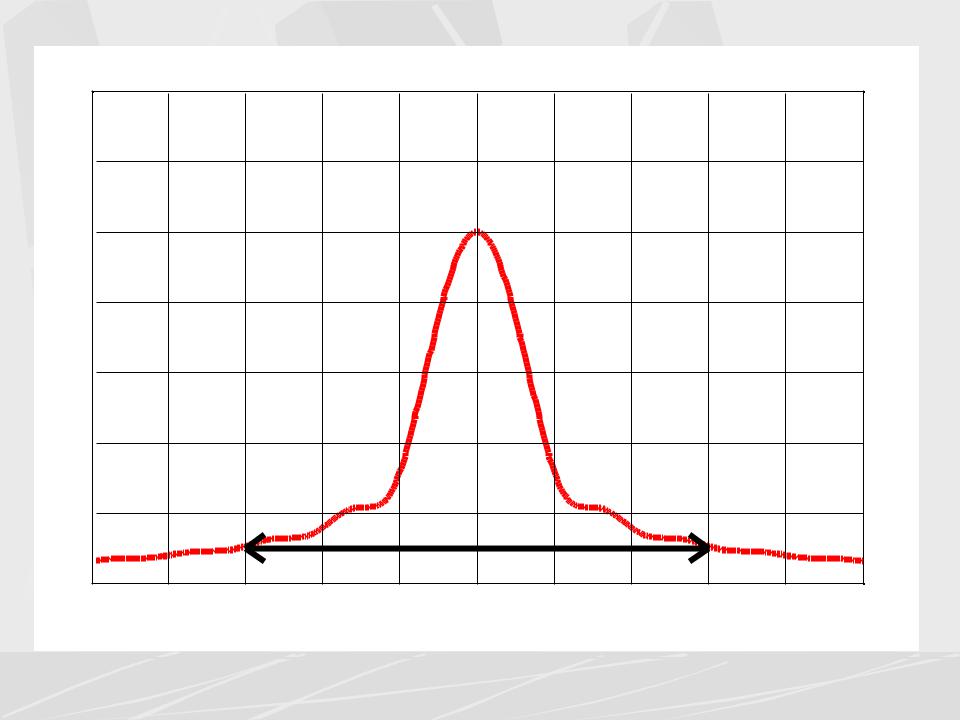
Triangular pulse AFC
|
|
|
|
A( ) |
|
|
|
|
|
|
1 |
|
|
T/2 |
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
T |
8 |
6 |
4 |
2 |
2 |
4 |
6 |
8 |
|
||
|
|
|
|
|
|
|
|
|
|
26 |
|
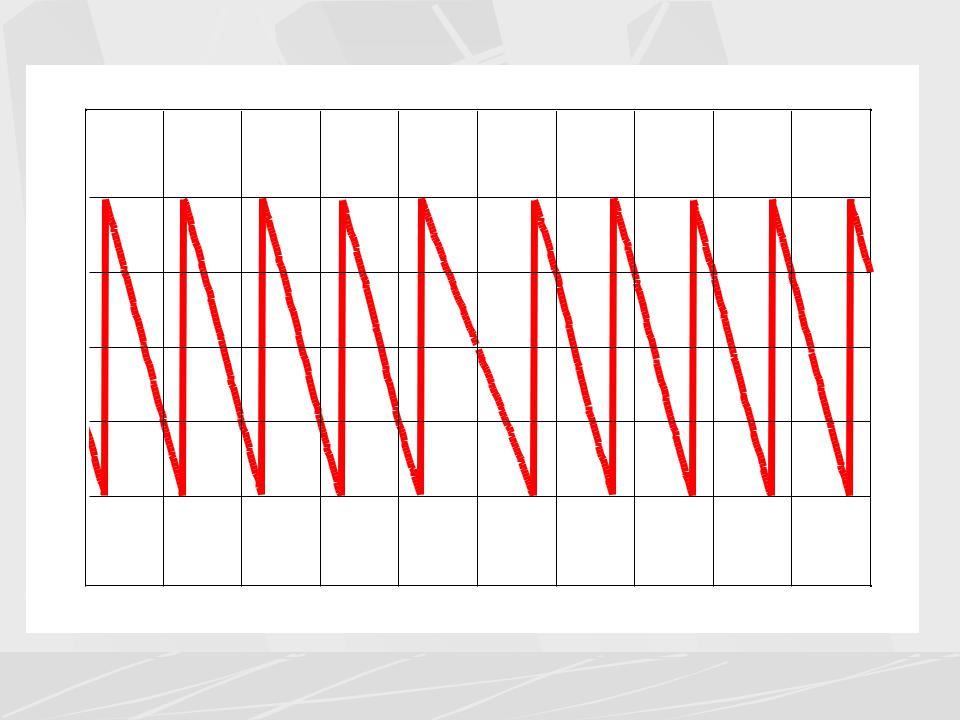
Triangular pulse PFC |
|
|
|
||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
6 4 2 |
0 2 |
4 |
6 |
8 |
T |
|
|
|
|
|
|
27 |
Этот амплитудный спектр (АЧХ) не содержит ярко выраженных лепестков, поэтому для определения эффективной ширины спектра необходим иной критерий. Будем определять эффективную ширину спектра по уровню 0.1 от максимума. Из графика видно, что эта ширина (она показана стрелкой) составляет примерно
6 / T
Так как длительность треугольного сигнала равна
t T |
, |
|
то база треугольного сигнала равна
t 6
28
Односторонний экспоненциальный импульс
У рассмотренных импульсов ФЧХ имела резкий пилообразный характер. Мы рассмотрим сейчас импульс, у которого ФЧХ имеет гладкую зависимость. Рассмотрим односторонний экспоненциальный импульс
|
|
a t |
, |
t 0, |
s(t) e |
|
|||
|
0, |
|
t 0 |
|
где a 0 произвольное положительное число. |
|||
Вычисляем спектр S( ) с помощью прямого преобразования |
|||
Фурье |
|
1 |
|
|
|
||
|
S( ) e a t e i t d t |
|
|
|
a i |
||
|
0 |
||
29
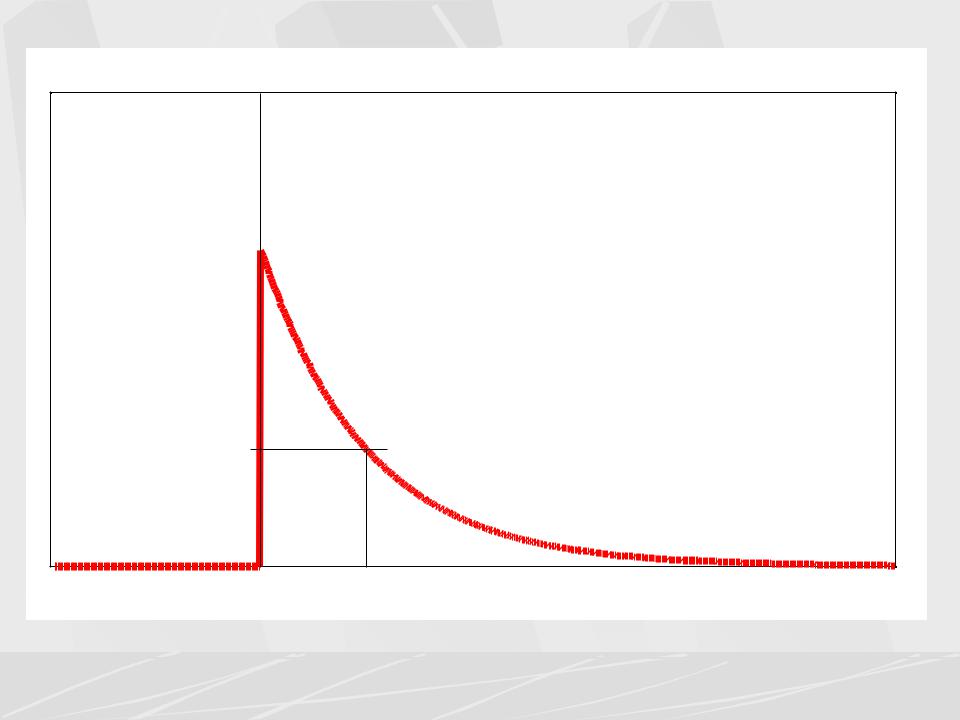
Exponential pulse
s(t) |
|
|
1 |
|
|
1/e |
|
|
0 |
1/a |
t |
|
|
30 |
|
|
|
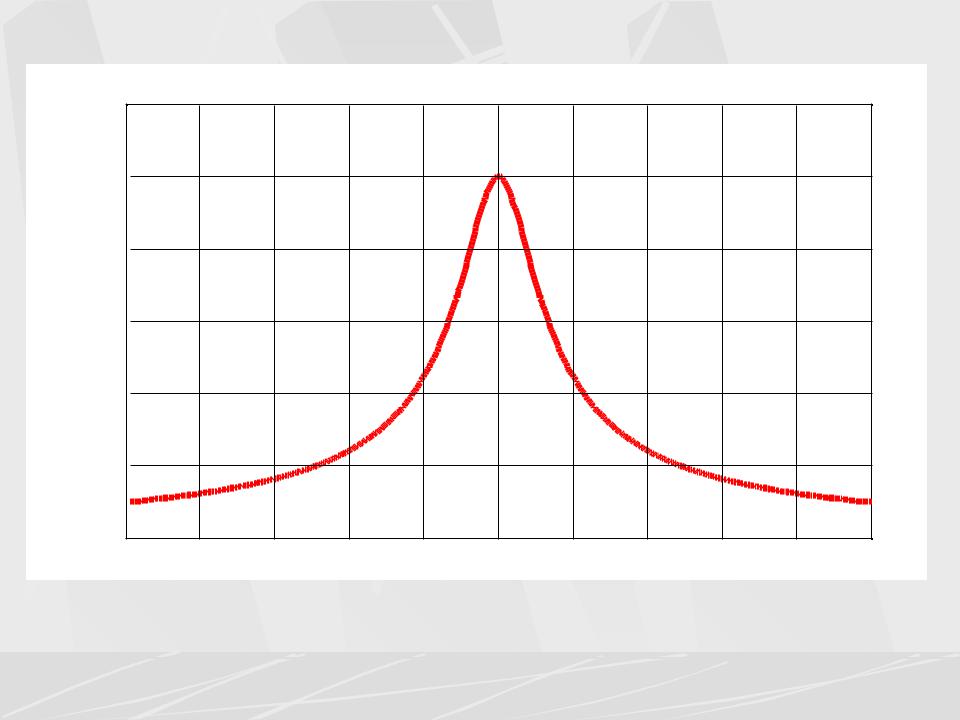
Exponential pulse AFC |
|
|
|
|||||
|
|
|
|
|
A( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1/a |
|
|
|
|
|
|
|
|
|
|
|
1/5a |
|
|
|
|
|
|
|
|
|
|
|
10 |
8 |
6 |
4 |
2 |
0 |
2 |
4 |
6 |
8 |
/a |
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
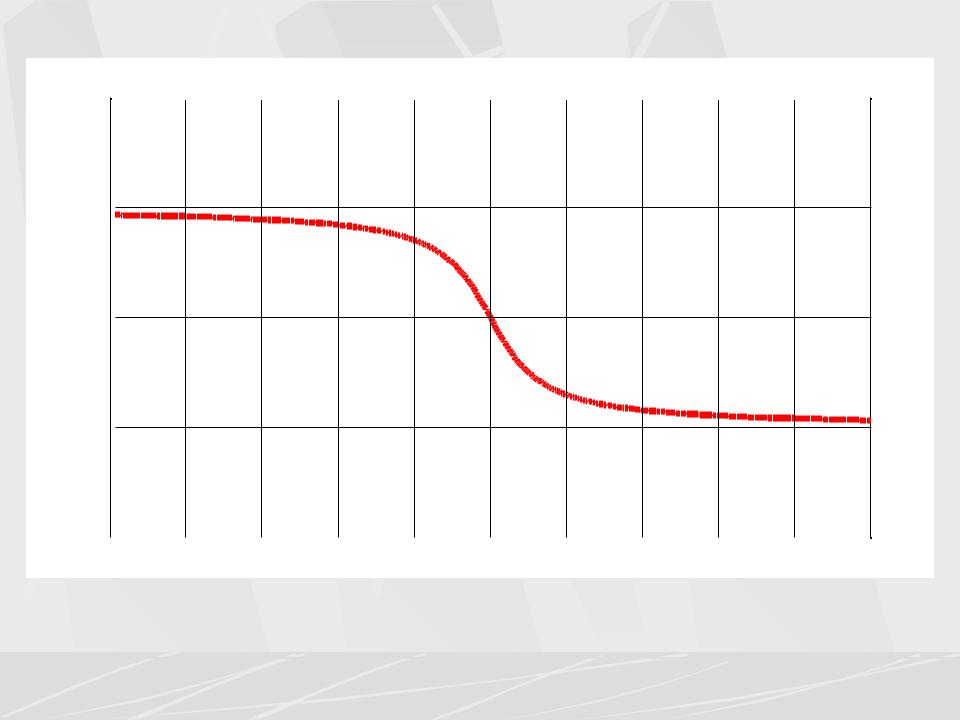
Exponential pulse PFC |
|
|
|
|
|
( ) |
/2
0
/2
10 |
|
|
|
/a |
8 6 4 2 |
0 2 4 6 |
8 |
32