Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Дальневосточный федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Обработка изображений / Лекции по обработке изображений Ч 1

.pdf

Скачиваний:

161

Добавлен:

25.04.2015

Размер:

1.73 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Министерство образования и науки Российской Федерации Дальневосточный федеральный университет

Кафедра компьютерных систем

ОБРАБОТКА ИЗОБРАЖЕНИЙ

Учебное пособие

В2 частях

Часть I

Оптические системы обработки изображений

Учебное электронное издание

Владивосток Издательский дом Дальневосточного федерального университета

2013

УДК 004.9

ББК 73

О-23

Рецензенты: Е. Л. Кулешов, д.т.н., наук, профессор, зав. кафедрой компьютерных систем ДВФУ; П.Н. Корнюшин, д.ф.-м.н., профессор,

зав. кафедрой компьютерной безопасности ДВФУ

Составители:

Б.Н. Грудин, В.С. Плотников, С.В. Полищук

Обработка изображений [Электронный ресурс] : учеб. пособ. О-23 В 2 ч. Ч. 1. Оптические системы обработки изображений / [cост.:

Б.Н. Грудин, В.С. Плотников, С.В. Полищук]; Дальневосточный федеральный университет. – Электрон. дан. – Владивосток: Издательский дом Дальневост. федерал. ун-та, 2013. – Режим доступа:

Computer university network. – Загл. с экрана.

В первой части учебного пособия рассматриваются аналоговые оптико-электронные системы – обработки изображений. Изложены математические основы описания непрерывных изображений с использованием теории линейных систем и преобразования Фурье. На основе физической оптики и радиооптического подхода к физике дифракции рассмотрены системы спектрального анализа, пространственночастотной фильтрации и визуализации изображений в когерентной оптике.

Пособие предназначено для студентов, обучающихся по направлениям «Информатика и вычислительная техника», «Информационные технологии», «Компьютерная безопасность», а также будет полезно специалистам по оптическим системам обработки изображений и компьютерной микроскопии.

УДК 004.9

ББК 73

ОГЛАВЛЕНИЕ Ведение……………………………………………………………………………4

1. Математическое описание непрерывных
(аналоговых) изображений.................................................................................	4
1.1. Двумерное преобразование Фурье .................................................................	5
1.2. Анализ линейных систем с помощью преобразования Фурье ....................	6
2. Распространение световых волн в свободном пространстве ...................	7
2.1. Построение общего решения волнового уравнения.....................................	7
2.2. Частотная характеристика и отклик свободного пространства ................	10
2.4. Решение дифракционных задач. Приближение Кирхгофа ........................	14
2.4. Дифракция Френеля и дифракция Фраунгофера ........................................	14
3. Линзы как элементы, выполняющие преобразование Фурье...............	18
3.1.Модуляционные характеристики оптических элементов ...........................	18
3.2 Техническая реализация оптического когерентного
спектрального анализатора. ...........................................................................	22
3.3. Оптико-цифровое вычислительное устройство
для спектрального анализа изображений .....................................................	25
4. Формирование изображения в когерентной оптической системе ........	28
4.1. Получение изображений................................................................................	28
4.2. Аберрации и их влияние на частотный отклик...........................................	31
5. Фильтрация изображений в когерентной оптике ....................................	34
5.1. Процессор с двумя линзами ..........................................................................	34
5.2. Пространственно-частотные фильтры .........................................................	38
5.3. Голографические пространственно-частотные фильтры...........................	40
5.4. Метод Ломана в записи цифровых фурье-голограмм ................................	45
5.5. Моделирование на ЭВМ многокомпонентной когерентной оптической
системы...................................................................................................................	46
6. Визуализация фазовых объектов .................................................................	50
6.1. Преобразование Гильберта ...........................................................................	50
6.2. Теневые приборы ...........................................................................................	51
6.2.1. Фильтр Цернике ..........................................................................................	52
6.2.2. Нож Фуко .....................................................................................................	53
6.2.3. Фазовый нож................................................................................................	54
6.2.4. Визуализация фаз при дефокусировке......................................................	55
6.2.5. Метод дефокусировки для «слабофазовых объектов»............................	56
6.3. Формирование изображений в электронном микроскопе .........................	58
Список литературы ............................................................................................	60

Введение

Многие отрасли техники, имеющие отношение к получению, обработке, хранению и передаче информации, в значительной степени ориентируются в настоящее время на развитие систем, в которых информация имеет характер изображений. Изображение, которое можно рассматривать как двумерный сигнал, является значительно более емким носителем информации, чем обычный одномерный (временной) сигнал. Вместе с тем, решение научных и инженерных задач при работе с визуальными данными требует особых усилий, опирающихся на знание специфических методов, поскольку традиционная идеология одномерных сигналов и систем мало пригодна в этих случаях. В особой мере это проявляется при создании новых типов информационных систем, решающих такие проблемы, которые до сих пор в науке и технике не решались, и которые решаются сейчас благодаря использованию информации визуального характера.

Современные системы обработки изображений можно разделить на три класса: аналоговые (оптические), цифровые и аналогово-цифровые (оптикоцифровые). В аналоговых системах обработки изображений используются когерентные и некогерентные оптические вычислительные устройства. Цифровая обработка изображений предполагает использование ЭВМ. В гибридных оптико-цифровых системах используются ЭВМ и оптические процессоры. Изучение методов и систем обработки и анализа изображений начнем с рассмотрения математического аппарата, используемого при аналоговой (оптической) обработке.

Оптические системы обработки изображений получили широкое распространение после изобретения в начале 60-х годов прошлого века источников когерентного света – лазеров. Обработка изображений в таких системах основана на возможности реализации в них различных математических преобразований и операций над изображениями, в частности, преобразования Фурье. При изложении основ вычислительной оптики мы будем использовать радиооптический подход. Этот подход основан на применении хорошо разработанного математического аппарата теории колебаний для объяснения другого круга вопросов – волновых явлений.

1. Математическое описание непрерывных (аналоговых) изображений

Для простоты будем во всех случаях описывать изображение, сформированные некоторой физической системой, с помощью функции

f (x, y,t) 0 . Для одноцветной системы функция f (x, y,t) представляет собой распределение яркости или какой-либо другой физической величины,

связанной с яркостью. Для цветных изображений f (x, y,t) есть одна из

координат цвета, которые пропорциональны интенсивностям красного (R), зеленого (G) и синего (В) цвета, смесь которых дает заданный цвет. Во многих системах воспроизведения изображений изображение не меняется во времени и переменная t может быть опущена (статические изображения). Мы в основном будем рассматривать именно такие изображения. Иногда для простоты изложения некоторые методы обработки и анализа демонстрируются для одномерных изображений f (x) . Большое значение в

обработке изображений имеют операция свертки и преобразования Фурье, относящиеся к классу интегральных преобразований.

1.1. Двумерное преобразование Фурье

Пусть задана комплексная функция двух переменных f (x, y) . По

определению

преобразованием

Фурье

F f (x, y)

этой

функции

будет

комплексная функция F(u1 ,u2 )

F (u1 ,u2 ) F f x, y

f x, y exp[i(u1 x u2 y)]dxdy .

(1.1)

u1 ,u2

Переменные

называются

пространственными частотами. Как и в

одномерном случае, справедливо обратное преобразование

f (x, y) F -1 F u1 ,u2

F (u1 ,u2 )exp[i(u1 x u2 y)]du1du2 .

(1.2)

Соотношение

(1.2)

можно

рассматривать

как

представление

функции f (x, y)

виде линейной

комбинации элементарных функций

exp i(u1 x u2 y ,

а спектр Фурье

F(u1 ,u2 )

как набор комплексных весовых

множителей, на которые следует помножать каждую из элементарных функций, чтобы получить исходную функцию f (x, y) .

Свойства преобразования Фурье, справедливые в одномерном случае, справедливы и для двумерных полей – изображений. В частности, если

F(u1 ,u2 ) и G(u1 ,u2 ) – фурье-образы						функций								f (x, y) и g(x, y) ,	а, b –
действительные числа, то
		F f (ax, by)				1		u	1		u	2
							F		1	,		2	,		(1.3)
							F			,			,		(1.3)
					ab			a			b
		F f (x a, y b) e i ( au1 bu2 ) F(u1 , u2 ) ,													(1.4)


F	f ( , )g(x , y )d d F (u1 , u2 )G(u1 , u2 ) ,														(1.5)

			2 dxdy	1										2 du1 du2 ,
		g(x, y)		1				G(u1 , u2 )							(1.6)
		g(x, y)		2				G(u1 , u2 )							(1.6)
				4



F		f ( , )g(x , y )d d F (u1 , u	2 )G(u1 , u2 ) ,	(1.7)

		f (x, y) F -1 F f x, y FF -1 f x, y .		(1.8)

Пусть	функция f (x, y) f ( x2 y2 ) f (r) .		Тогда, осуществляя в

плоскостях координат и частот переход к полярным координатам по формулам:

r 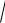x 2 y 2 , x r cos , y r sin ,

u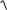u1 2 u2 2 , u1 u cos , u2 u sin ,

иучитывая, что якобиан перехода от декартовых координат к полярным равен r, получаем следующее выражение для фурье-образа функции f (r) :

f (r) rf r dr exp iur cos( d . (1.9)

0 0

Используя формулу для интегрального представления функции Бесселя первого рода нулевого порядка

		1	2
I 0	a	1	exp ia cos( d ,	(1.10)
I 0	a	2	exp ia cos( d ,	(1.10)
		2	0
получаем

	F f (r) 2 rf r I 0 (ur) dr .			(1.11)
			0

Преобразование вида (1.11) называется преобразованием Фурье-Бесселя.

1.2. Анализ линейных систем с помощью преобразования Фурье

Для линейной системы, представляющей собой “черный ящик”, выходное изображение g(x, y) может быть получено в результате действия

линейного оператора Т на входное изображение f (x, y) , то есть

	g(x, y) T f x, y .	(1.12)
Равенство (1.12) можно записать в виде

g x, y T[ f ( , ) (x , y )d d ]


	f ( , )T[ (x , y )]d d .	(1.13)

Функцию h(x, y; , ) T[ (x , y )] называют импульсным		откликом

системы. Теперь выходное изображение может быть представлено в виде интеграла суперпозиции


g x, y	f ( , )h(x, y; , )d d .	(1.14)

Линейная система называется пространственно-инвариантной,		если

h(x, y; , ) h(x , y ) . В этом случае интеграл суперпозиции становится интегралом свертки


g x, y	f ( , )h(x , y )d d .	(1.15)

Оптические системы, формирующие изображения, как правило, пространственно-инвариантны.

Осуществляя преобразование Фурье от обеих частей равенства (1.15) и используя теорему свертки, получаем

G(u1 , u2 ) F(u1 , u2 )H (u1 , u2 ),	(1.16)
где G(u1 ,u2 ) F g(x, y) , F(u1 ,u2 ) F f (x, y) , H (u1 ,u2 ) F h(x, y) .

Выполняя обратное преобразование Фурье от обеих частей равенства (1.16), находим

	1
g(x, y)			F (u1 ,u2 )H (u1 ,u2 )exp[i(u1 x u2 y)]du1du2 ,	(1.17)
	4	2

т.е. изображение на выходе линейной системы может быть получено в результате обратного преобразования Фурье от произведения спектра входного изображения на частотную характеристику системы.

2. Распространение световых волн в свободном пространстве

2.1. Построение общего решения волнового уравнения

Распространение света в пространстве описывается уравнениями Максвелла:

rotE

H y

J ,

rotH

divD

E , B

0 H ,

0 E .

Здесь: E

–

напряженность

электрического

поля,

H - напряженность

магнитного

поля,

–

вектор

электрической индукции,

–

вектор

магнитной индукции,

– плотность электрических зарядов,

плотность

тока, – проводимость,

0 -

диэлектрическая проницаемость

вакуума, –

относительная диэлектрическая проницаемость среды, в которой распространяется свет, 0 - магнитная проницаемость вакуума, –

относительная магнитная проницаемость среды, в которой распространяется

					0 ,		0			1,	1,
свет. В вакууме в отсутствии	токов и	зарядов:		j	0 ,		0			1,	1,

divD 0. Вычислим:
								2
rotrot E 2 E graddiv E			rot H						E .
rotrot E 2 E graddiv E			rot H				0 t 2		E .
		0 t				0	0 t 2

Отсюда получаем, что распространение света в вакууме описывается волновым уравнением:

			1		2
		2 E				E .
			c2	t 2

Здесь c 1/	0 0 – скорость		света			в вакууме. Аналогичное уравнение

несложно получить и для напряженности магнитного поля. Таким образом, распространение света в вакууме описывается скалярным волновым уравнением вида


	2U (r , t)
где 2
где 2	– оператор Лапласа; U (r ,t)

1	2
		U (r , t)	,	(2.1)
c 2		t 2

– скалярное волновое поле (или одна из

составляющих векторного поля); r - координата; t - время; c - скорость света. Для монохроматического света частное решение волнового уравнения ищем в виде

		(2.2)
U (r , t) a(r ) exp(i t) ,

где a(r ) - независящая от времени амплитуда, - частота. Подставляя (2.2) в

(2.1), получаем

(

0 ,

(2.3)

)a(r )

т.е. комплексная амплитуда

a(r ) удовлетворяет уравнению Гельмгольца.

Константа k в уравнении (2.3),

называемая волновым числом,

связана с

длиной волны света в свободном пространстве соотношением

k 2 / / c .

(2.4)

Простое нетривиальное решение уравнения (2.3)

a r b exp( i

x k

) exp( ikr ) b exp( i

) exp[ i(k

z)],

(2.5)

где b – амплитуда, 0

– фаза комплексной амплитуды

a r , а

kx , k y , kz –

проекции волнового вектора на оси координат. Это решение (его реальная

часть) представляет собой плоскую монохроматическую волну,

распространяющуюся в направлении, определяемом вектором k . В общем случае направление распространения определяется двумя углами и 0 .

Если эти углы выбраны по отношению к прямоугольной системе координат

x, y, z , как показано на рис.2.1, то

kx k sin , u2

k y k cos sin ,

kz k cos cos .

(2.6)

Выражая kz

через ( u1 ,u2 ), получаем

k 2

u 2 u 2 .

(2.7)

Подставляя (2.6), (2.7) в (2.5), находим

a x, y, z b exp i

exp iz

exp i u

y .

k 2 u 2

x u

(2.8)

Воспользуемся частным решением (2.8) уравнения (2.3) для построения общего решения уравнения Гельмгольца.

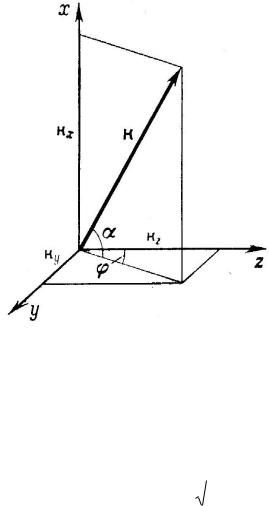
Рис. 2.1. К выбору системы координат в свободном пространстве

Поскольку уравнение (2.3) линейно, то его решение будет суммой полей вида (2.8). Такое решение можно записать в виде интеграла от (2.8) по независимым параметрам плоских волн, которыми являются их амплитуды, фазы и направления распространения. Интеграл имеет вид

p x, y, z	1
					2 u2	2 )
			g(u1 ,u2 ) exp( iz	k 2 u1
	4	2					(2.9)

exp[i(u1 x + u2 y)]du1du2 ,

где g u1 , u2 - комплексная функция, которая описывает амплитуду и фазу

отдельной плоской волны с направлением распространения, определяемым совокупностью действительных переменных (u1 ,u2 ), называемых

пространственными частотами. Здесь и далее, где не оговорено особо, интегрирование осуществляется в пределах от до .

Пусть в плоскости z 0 заданы значения волнового поля				p x, y, z , т.е.
его комплексная амплитуда. Тогда
	1		exp i u1 x u2 y du1 du2 .
p x, y,0	1	g u1 , u2		(2.10)
p x, y,0	2	g u1 , u2		(2.10)
	4

Выражение (2.10) представляет собой интеграл Фурье. Обратное преобразование Фурье позволяет найти функцию g u1 ,u2 :


g u1 , u2 p x, y,0 exp i u1 x u2 y dxdy .	(2.11)

Решение (2.9) остается двузначным, поскольку можно выбрать любой из двух знаков перед координатой z . При z 0 затухающие по физическому смыслу

неоднородные волны, для которых u 2	u 2	k 2	, получаются, если выбираем
1	2		случае функция g u1 ,u2
в (2.9) перед z знак «+». В одномерном			случае функция g u1 ,u2
			9

определяется соотношением


	g(u) p(x, y,0)exp( iux)dx				(2.12)

и, соответственно,
	1
	1
p(x, z)			g(u) exp(iz	k 2 u 2 ) exp(iux)du.	(2.13)
p(x, z)		2	g(u) exp(iz	k 2 u 2 ) exp(iux)du.	(2.13)
		2
В качестве важного			частного случая разложения (2.9)		рассмотрим

разложение сферической волны по плоским волнам. Комплексная амплитуда сферической волны

p x, y, z exp ikR

R ,

(2.14)

Очевидно, что p x, y,0 exp ikr r , где

где R

y2 z 2 .

r x2

y2 .

Функцию g(u1 ,u2 ) найдем, используя преобразование Фурье – Бесселя

g(u) 2 exp(ikr)I 0 (ur) dr ,

(2.15)

где u

u 2

u 2 . Известно, что такой интеграл равен

g u , u

2 i

k 2

2 u

2 .

(2.16)

Подставляя (2.16) в (2.9), получаем

exp[i(u1 x u2 y z

k 2

u1 2

2 )]

exp(ikR)/R

du1 du2 .

(2.17)

2.2. Частотная характеристика и отклик свободного пространства

Аналогия между колебательными и волновыми процессами основывается на том, что как те, так и другие описываются линейными дифференциальными уравнениями и совершаются в так называемых «линейных системах». Реакция линейной системы y t на некоторое входное

воздействие x t выражается либо как

y t	1
	1	Cx ( )H ( )exp(i t)d ,		(2.18)
		Cx ( )H ( )exp(i t)d ,		(2.18)
	2
либо как

	y t x t h t t dt ,			(2.19)

где Cx – спектр входного воздействия, определяемый выражением

Cx x t exp i t dt ,				(2.20)

		1
x(t)		1	Cx ( )exp(i t)d .	(2.21)
x(t)			Cx ( )exp(i t)d .	(2.21)
		2

H ( ), h(t) , соответственно, частотная и импульсная характеристики линейной системы, которые связаны между собой парой преобразования

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в папке Обработка изображений

#
25.04.20151.6 Mб137Л.Р. по обработке изображений Ч. 1.pdf
#
25.04.20152.67 Mб156Л.Р. по обработке изображений Ч. 2.pdf
#
25.04.20151.73 Mб161Лекции по обработке изображений Ч 1.pdf
#
25.04.20156.34 Mб275Лекции по обработке изображений Ч 2.pdf