Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский технологический университет "МИСиС"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matan / Лекц3-6a.ppt

Скачиваний:

Добавлен:

20.04.2015

Размер:

1.42 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекция 3.6

Приложения формулы Тейлора к вычислению пределов, выделению главной части функции и исследованию поведения функции в окрестности точки.

Правило Лопиталя раскрытия неопределенностей.

Вычисление пределов с помощью формулы Тейлора.

Рассмотрим сначала случай неопределенности вида 0 .

	Пусть требуется найти предел		f (x)
		lim		,
			g(x)
где		x x0
	lim f (x) lim g(x) 0.
	x x0	x x0

Разложим по формуле Тейлора функции f(x) и g(x) в окрестности точки x0, ограничившись лишь первыми не равными нулю членами, то есть

f(x) = a(x – x0)n + o((x – x0)n),			a ≠ 0,
g(x) = b(x – x )m + o((x – x		)m),	b ≠ 0.
0	0

Тогда f (x)

a(x

x0 )n o((x

x0 )n )

lim

g(x)

b(x

x0 )

o((x

x0 )

)

x x0

x x

если

lim (x

x0 )

n m

если

x x0

если

lim	(x	x )n (a o(1))
lim		0	m
		0
x x0	(x	x0 )		(b o(1))
x x0

n m, n m, n m.

Часто бывает удобно для разложений функций f(x) и g(x) использовать готовый набор разложений элементарных функций по формуле Маклорена. Для этого в случае, когда x0 ≠ 0, следует предварительно сделать замену переменной, положив t = x – x0. Тогда t → 0 при x → x0.

ПРИМЕР 1.

o(x4 )

sin x shx

lim

1 .

lim

o(1)

lim

x 0

sin x

o(x4 ),

shx x

o(x4 ),

sin x shx

o(x

)

o(x

)

o(x

Случай x → ∞ сводится заменой переменной x = 1/t к случаю t → 0.

ПРИМЕР 2.
lim x7 / 4 4								4								24
lim x7 / 4 4				x 1				4				x 1				24							x
x


f (x) x		7 / 4	4	x 1						4	x 1						2		4		x											1					1								1
		7 / 4	4							4									4						x		2		4	1		1			4	1	1			2		положим			1		t
																									x					1		x				1		x		2	;	положим				x	t
																																x						x								x
			1/ 4		(1						1/ 4						2													3	t2 o(t2 )												3					3
			1/ 4								1/ 4																				t2 o(t2 )
lim	(1 t)								t)												lim								16											lim				o(1)					.

						t	2
							2																									t	2
t 0																							t 0										2							t 0 16								16
																							t 0																	t 0 16								16
											1				(		1			1)
	(1 t)1/ 4 1									1 t			4		(		4			1)		t2 o(t							2 ) 1					1 t			3		t 2 o(t 2 );
	(1 t)1/ 4 1									1 t							2!					t2 o(t							2 ) 1					1 t			32		t 2 o(t 2 );
										4							2!																	4			32
											1							1
	(1 t)1/ 4 1									1 t				4 (				4		1)				t2 o(t 2 ) 1												1 t				3	t 2 o(t2 );
	(1 t)1/ 4 1									1 t								2!						t2 o(t 2 ) 1												1 t			32		t 2 o(t2 );
										4								2!																		4			32
				1/ 4							1/ 4												3						2					2
	(1 t)					(1 t)											2											t		o(t					).
	(1 t)					(1 t)											2									16		t		o(t					).

При раскрытии данным методом неопределенностей вида ∞/∞, 0·∞ и ∞ – ∞ их следует преобразовать к неопределенности вида 0/0.

Для раскрытия неопределенностей вида 00, ∞0, 1∞ необходимо предварительно прологарифмировать рассматриваемые функции.

ПРИМЕР 3.


		1
lim sin x
			x2
	x
x 0

lim

sin x

lim

o(1)

e 1/ 6.

ex 0

1			sin x	1			x		x3	o(x4 )					1			x2							1				x2
1			sin x	1			x	6		o(x4 )					1			x2			3				1				x2						2
		ln				ln											ln(1			o(x		))										o(x				)
	2	ln			2	ln										2	ln(1			o(x		))				2						o(x				)
x			x	x						x					x			6							x					6
x			x	x						x					x			6							x					6
ln(1			t) t								x	2	o(x	3	)		o		x	2	o(x		3	)			x	2			o(x		2	)



				o(t)
										6								6									6
										6								6									6

Приложения формулы Тейлора к исследованию поведения функции в окрестности точки.

В качестве примера применения формулы Тейлора для исследования поведения функции в окрестности точки приведем доказательство третьего достаточного условия экстремума, использующего производные высших порядков.

ТЕОРЕМА.

Пусть существует f (n)(x0), где n > 2, и выполняются условия:

f ´(x0) = f ´´(x0) = … = f (n-1) (x0) = 0, f (n) (x0) 0.

Тогда

Если n = 2k, то х0 – точка локального экстремума функции, а именно:

•f (n) (x0) < 0 – точка строгого локального максимума.

•f (n) (x0) > 0 – точка строгого локального минимума;

Если n = 2k+1, то x0 – не является точкой экстремума функции.

Доказательство.

Формула Тейлора n-ого порядка для функции f(x) в данном случае имеет вид:

f(x) = f(x0) + f (n)( x0)(x – x0)n/n! + о((x – x0)n). Отсюда получим

f(x) – f(x0) = f (n)( x0) /n! (1+ о(1)) (x – x0)n.

Если n = 2k, то (x – x0)n > 0 и разность f(x) – f(x0) имеет знак производной, то есть

f(x) < f(x0), если f (n) (x0) < 0, и х0 – точка локального максимума, f(x) > f(x0), если f (n) (x0) > 0, и х0 – точка локального минимума.

Если n = 2k + 1, то (x – x0)n имеет разные знаки в левой и правой полуокрестности точки x0, то есть разность f(x) – f(x0) меняет знак при переходе через точку x0. Это означает, что эта точка не является точкой экстремума.

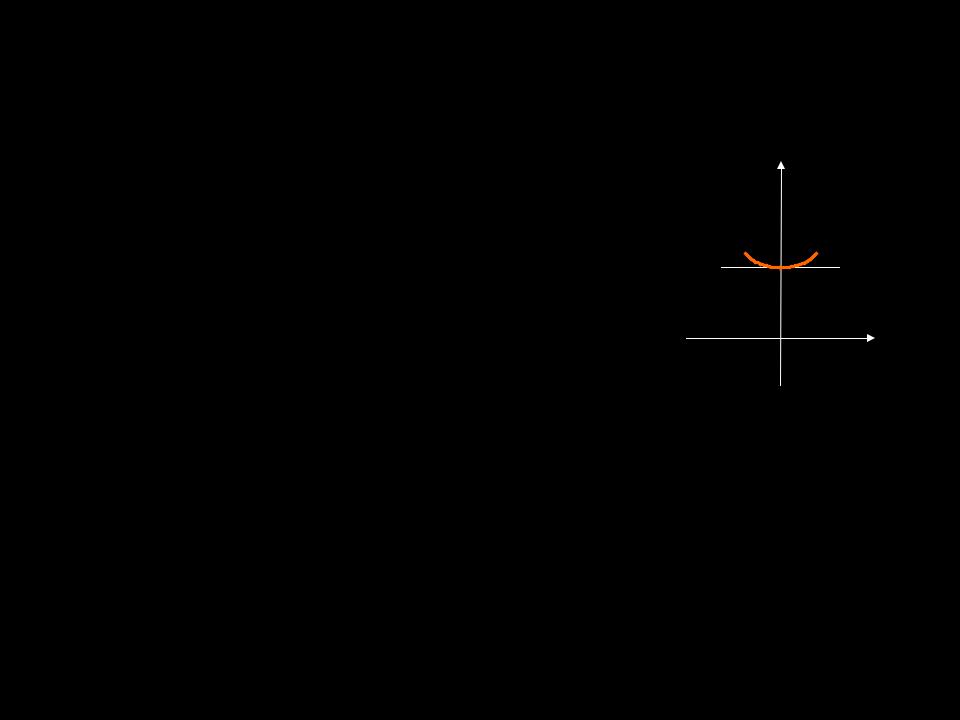
ПРИМЕР.		y cos x chx
Исследуем поведение функции		y cos x chx
в окрестности точки x0 = 0.
y sin x shx,	y (0) 0;		y
y cos x chx,	y (0) 0;			y = f(x)
y cos x chx,	y (0) 0;
y(3) sin x shx,	y(3) 0;			2
y(3) sin x shx,	y(3) 0;
y(4) cos x chx,	y(4) (0) 2	0.	0	x
y(4) cos x chx,	y(4) (0) 2	0.

Согласно третьему достаточному условию экстремума, точка x0 = 0 является точкой локального минимума функции. Значение функции в этой точке f(0) = 2.

Разложение функции по формуле Маклорена имеет вид:

f (x) 2 42! x4 o(x4 ).

Гиймон Франсуа Лопиталь (1661-1704 )

Родился в Париже в богатой и знатной семье. Носил звание маркиза (де Сен-Мэм) и графа (Антрмон). Служил капитаном кавалерии. Оставив военную службу из-за близорукости, посвятил себя математике. Ученик Иоганна Бернулли.

В 1693г. Лопиталя избрали членом Парижской академии наук.

В 1696г. вышло из печати главное творение его жизни – «Анализ бесконечно малых для познания кривых линий». Это был первый печатный учебник по дифференциальному исчислению.

Скончался от апоплексического удара 43 лет от роду.

Неопределенность вида 0

ТЕОРЕМА 1.

Пусть функции f(x) и g(x) дифференцируемы на интервале (a, b),

lim f (x) 0,	lim g(x) 0,
x a 0	x a 0

g'(x) 0 для всех х (a, b) и существует (где А – число или бесконечность)

		lim	f '(x)	A.
		x а 0 g'(x)				f(x)
Тогда существует					y	f(x)
					y
lim	f (х)	A.					g(x)
lim	f (х)	A.
x a 0 g(х)
				0	a	b	x

1 / 21 2 > Следующая >>>

Соседние файлы в папке Matan

#
20.04.20151.1 Mб42Лекц2-3A.ppt
#
20.04.20151.18 Mб25Лекц2-4A.ppt
#
20.04.20151.22 Mб24Лекц2-5A.ppt
#
20.04.20151.34 Mб30Лекц3-1a.ppt
#
20.04.20151.28 Mб37Лекц3-5a.ppt
#
20.04.20151.42 Mб30Лекц3-6a.ppt
#
20.04.20151.16 Mб29Лекц3-7a.ppt
#
20.04.20151.24 Mб25Лекц4-4a.ppt
#
20.04.20151.14 Mб28Лекц4-5a.ppt
#
20.04.20151.55 Mб36Лекц4-6a.ppt
#
20.04.2015394.75 Кб45шпора по Матану.doc

Лекция 3.6

Вычисление пределов с помощью формулы Тейлора.

Приложения формулы Тейлора к исследованию поведения функции в окрестности точки.

Доказательство.

ПРИМЕР.

Гиймон Франсуа Лопиталь (1661-1704 )