Лекция 3.7

Условия выпуклости и условие

существования точек перегиба графика функции.

Общая схема исследования и

построения графиков функций одной переменной.

Направление выпуклости графика функции.

Пусть функция f(x) дифференцируема в любой точке интервала (а,b). Тогда существует касательная к графику функции, проходящая через любую точку М(x,f(x)) этого графика, причем эта касательная не параллельна оси Оу.

ОПРЕДЕЛЕНИЕ.

График функции f(x) имеет на интервале (а,b) выпуклость, направленную вверх (вниз), если в пределах этого интервала он расположен не выше (не ниже) любой своей касательной.

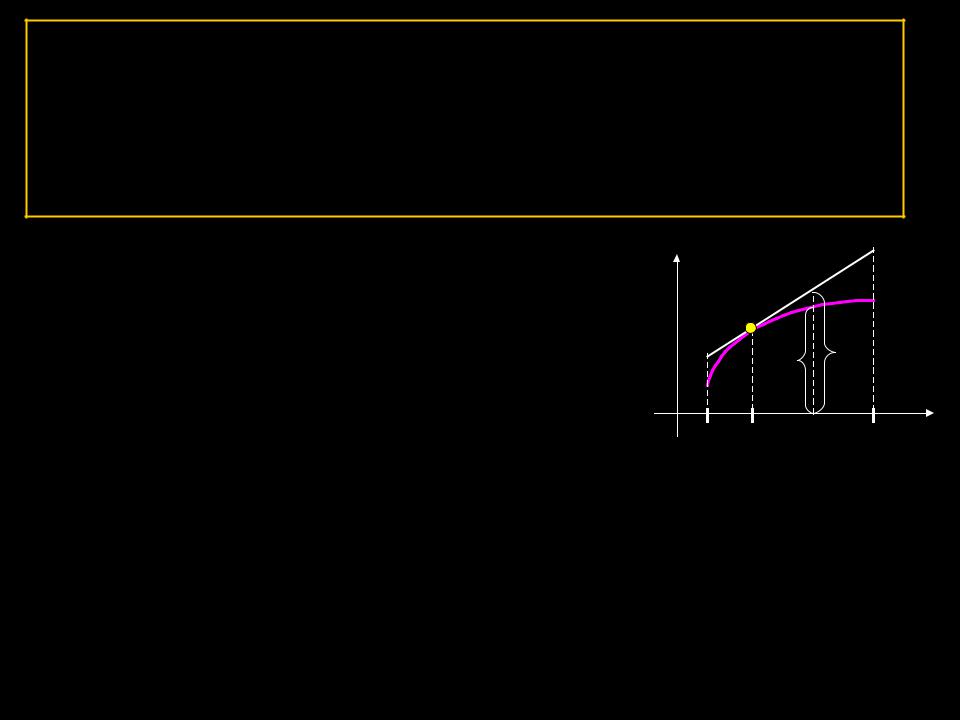
ТЕОРЕМА.

Если функции f(x) имеет на интервале (а, b) вторую производную и f ´´(x) 0 ( f ´´(x) 0)

во всех точках интервала, то график функции имеет на (а, b) выпуклость, направленную вверх (вниз).

Запишем для f(x) формулу Тейлора первого порядка в окрестности точки x0:

f(x) = f(x0) + f ( x0)(x – x0) + f ( )(х – x0)2/2. Отсюда следует, что

f(x) – Yкас = f ( )(х – x0)2/2 0

во всех точках интервала, то есть график лежит не выше касательной.

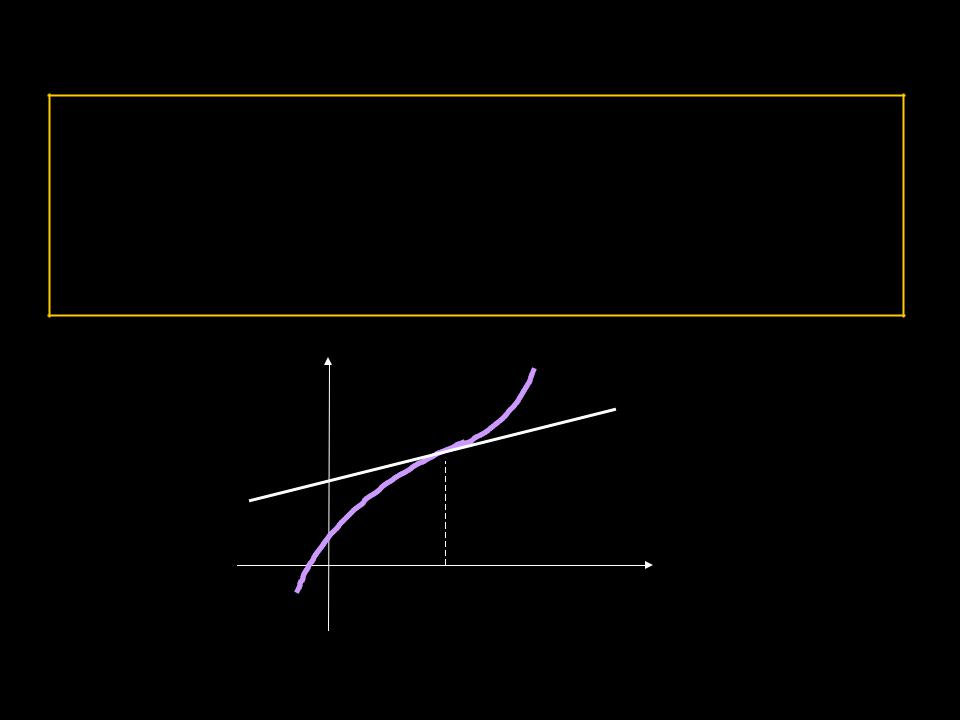
Точки перегиба графика функции.

ОПРЕДЕЛЕНИЕ.

Точка М( х0, f(х0 )) называется точкой перегиба графика функции

у = f(x), если в этой точке график имеет касательную и существует окрестность точки х0 оси ОХ, в пределах которой слева и справа от х0 график функции имеет разные направления выпуклости.

y = f(x)

y

М(хо, f(xo)) y0

ТЕОРЕМА (необходимое условие перегиба графика

функции, имеющей непрерывную вторую производную).

Если М(x0, f(x0)) точка перегиба графика функции у = f(x) и функция имеет в этой точке непрерывную вторую производную, то

f ´´(x0) = 0.

Доказательство.

Предположим, что f ´´(x0) 0.

Так как, по условию теоремы, f ´´(x) непрерывна в точке x0, то найдется такая окрестность этой точки, в которой f ´´(x) сохраняет знак числа f ´´(x0). Следовательно, функция сохраняет направление выпуклости в этой окрестности, что противоречит определению точки перегиба.

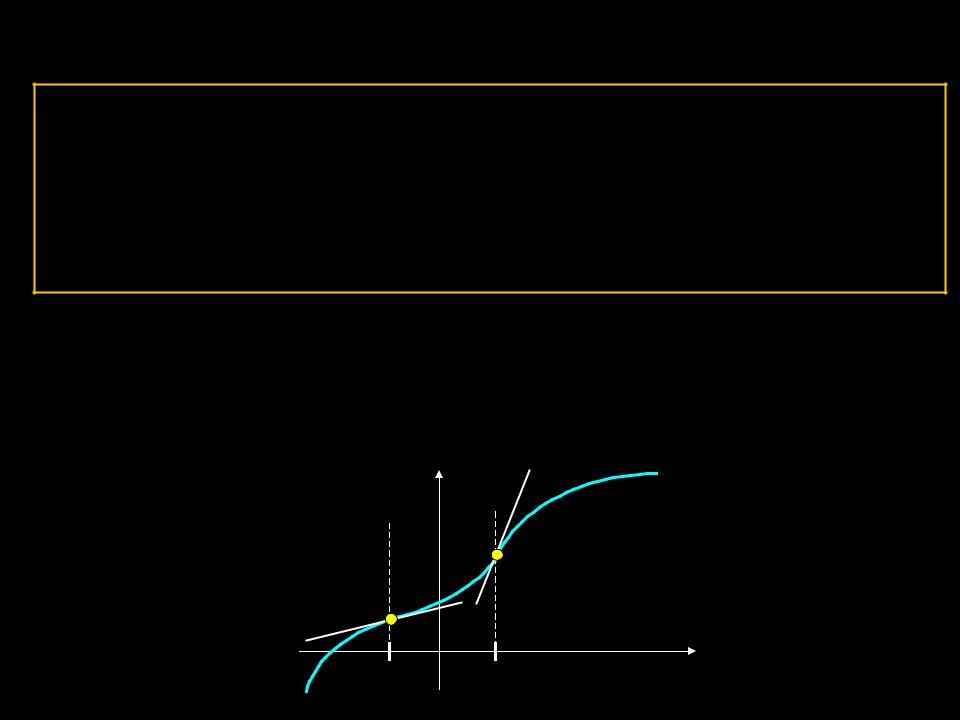
Достаточные условия перегиба.

ТЕОРЕМА 1.

Пусть у = f(x) непрерывна в точке x0, дважды дифференцируема в окрестности этой точки и график функции имеет касательную в точке М(x0, f(x0)). Если в пределах этой окрестности f ´´(x) имеет разные знаки слева и справа от x0, то М(x0, f(x0)) – точка перегиба графика функции.

Доказательство.

Так как f ´´(x) имеет разные знаки слева и справа от x0, то направление выпуклости слева и справа от точки различно, то есть М(x0, f(x0)) – точка перегиба графика функции.

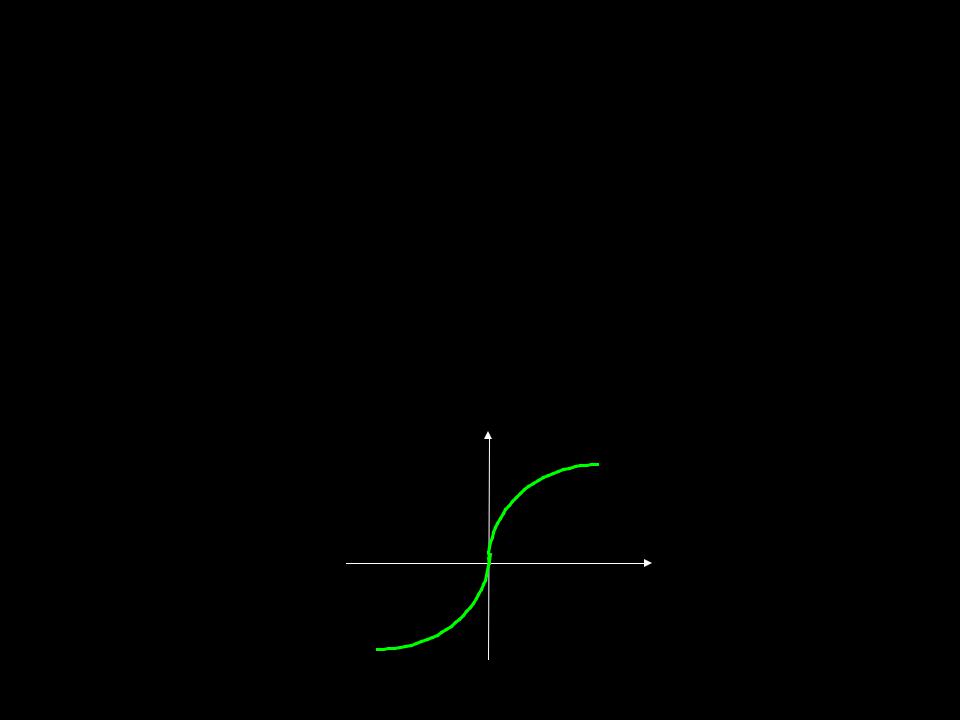
ПРИМЕР.

Найдем направления выпуклости и точки перегиба графика функции

y 3х.

Вычислим производные первого и второго порядка:

Здесь y (x) при х 0 и график функции в точке х = 0 имеет вертикальную касательную. Вторая производная в точке х = 0 не определена, а при переходе через эту точку меняет знак с плюса на минус. Итак, точка х = 0 – точка перегиба.

y

y < 0

Общая схема построения графика функции.

Изучение заданной функции f(x) и построение ее графика целесообразно проводить в следующем порядке:

Найти область определения функции. Выяснить, является ли функция четной, нечетной, периодической.

Найти точки пересечения графика с осями координат и промежутки, на которых f(x) > 0 и f(x) < 0.

Найти асимптоты графика.

Сделать приблизительный эскиз графика.

Вычислить первую производную, найти точки экстремума и промежутки возрастания (убывания) функции.

Вычислить вторую производную, найти точки перегиба и промежутки выпуклости вверх или вниз функции.

Окончательно вычертить график.

1.Область определения функции D(f) = (– , –1) (– 1, + ). Функция общего вида.

2.Найдем нули функции, решив уравнение

f(x) = 0 x = 0.

Отметим на числовой прямой промежутки знакопостоянства функции:

Знаки f(x)