20.В какой последовательности проводится проверка параметрической гипотезы?

Общая последовательность проверки гипотезы о параметрах

распределения такова:

- формулируются гипотезы Н0 и Н1;

- задается уровень значимости α;

- выбирается статистика Z для проверки Н0;

- определяется выборочное распределение статистики Z;

- в зависимости от Н1 определяется критическая область;

- вычисляется выборочное значение статистики z;

- принимается статистическое решение: если выборочное значение статистики z оказывается в области принятия решения, гипотеза Н0 принимается; если в критическую область гипотеза Н0 отклоняется, как несогласующаяся с результатами наблюдений.

21.Почему граница критической двухсторонней области определяется квантилями .?

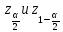Пусть, например, проверяется гипотеза о том, что параметр Θ распределения генеральной совокупности равен некоторому значению 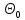, то есть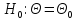. При этом возможны различные варианты альтернативных гипотез. Если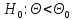, то критическая область расположена в левом «хвосте» соответствующего распределения, причем граница критической области определяется квантилью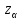(α – уровень значимости). Если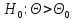, то критическая область – в правом «хвосте»; ее граница определяется квантилью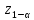. В этих двух случаях критическая область называется односторонней. Если же альтернативная гипотеза имеет вид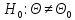, то имеем двухстороннюю критическую область, границы которой определяются соответственно квантилями.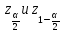

22.Как проверяется гипотеза о равенстве двух дисперсий, если известны математические ожидания? Неизвестны?

Пусть есть две независимые выборки значений нормально распределенной величины x: х₁, х₂,..., x_n - всего n элементов, и нормально распределенной величины y: y₁, y₂,..., y_m - m элементов.

Гипотеза Н₀ состоит в том, что дисперсии величин Х и У равны, т.е.

Н₀: Dx = Dy = s ² . (2)

Эта гипотеза проверяется по критерию, с которым нам еще предстоит познакомиться. Случайная величина

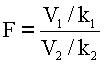, (3)

где ,, распределена по закону, получившему название "распределение Фишера".

У этого распределения два параметра k₁ и k₂, называемых числом степеней свободы для числителя и знаменателя. Очевидно, F принимает только положительные значения. Кроме того, F-распределение обладает одним очевидным свойством: если известна вероятность a того, что F > F_q (некоторого фиксированного числа), то, очевидно с такой же вероятностью 1/F<1/F_q , следовательно, с вероятностью 2a F выходит за пределы интервала (1/F_q , F_q). Поэтому таблицы F-распределения содержат только границы F_q>1 при заданном a и при определенных k₁, k₂ . Пользователь же должен помнить, что если экспериментальное значение критерия F окажется меньше 1, то его надо "перевернуть" и сравнить с табличным F_q обратную величину. Здесь приводятся таблица только для a =0.05. При необходимости введения других значений уровня значимости надо использовать более подробные статистические таблицы , в некоторых программных пакетах , например, в Mathcad , встроено вычисление F_q при любых a .

Подставив в F (3) в качестве V₁ комбинацию (n-1)*S_x²/Dx , которая, как было ранее показано, распределена по закону , а в качестве V₂ - (m-1)*S_y²/Dy , которая распределена по закону , получим, что в случае равенства дисперсий Dx и Dу (2) отношение

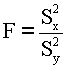(4)

подчиняется распределению Фишера, и, следовательно, может служить критерием проверки гипотезы о равенстве дисперсий (2).