- •Результаты
- •3.4.Проверка гипотезы о нормальности распределения по критерию хи-квадрат
- •3.5. Определение доверительных интервалов для математического ожидания и дисперсии генеральной совокупности
- •Контрольные вопросы
- •3.Как строится вариационный ряд?
- •4.Какое распределение называется выборочным?
- •5.Как строится гистограмма? Полигон? График выборочной функции распределения?
- •6.Как вычисляется выборочное среднее? Выборочная дисперсия? Выборочное стандартное отклонение?
- •7.В чем состоят особенности вычислений числовых характеристик для Группированного ряда?
- •8.Как определяется выборочная мода? Медиана?
- •9.Как определяется выборочный центральный момент?
- •10.Как вычисляется и что характеризует коэффициент асимметрии выборки? Коэффициент эксцесса?
- •12.Каковы точечные оценки математического ожидания и дисперсии?
- •13.В чем состоит метод максимального правдоподобия?
- •14.Доказать несмещенность и состоятельность выборочной средней как оценки математического ожидания.
- •15.Как определяется несмещенная дисперсия?
- •16.Перечислите основные распределения, используемые в статистических расчетах. Как определяются квантили этих распределений? От чего они зависят?
- •17.Используя таблицы, найти квантили
- •18.Как строится доверительный интервал для математического ожидания? Дисперсии?
- •19.Какая гипотеза называется нулевой? Альтернативной? в чем состоят ошибки первого и второго рода?
- •20.В какой последовательности проводится проверка параметрической гипотезы?
- •22.Как проверяется гипотеза о равенстве двух дисперсий, если известны математические ожидания? Неизвестны?
- •23.Какие критерии используются для проверки гипотез о виде распределения?
- •24.В чем состоит критерий хи-квадрат?
Контрольные вопросы
Что называется генеральной совокупностью?
Генеральной совокупностью называется вероятностное пространство (Ω,
F, Ρ), то есть пространство элементарных событий Ω с заданным на нем полем событий F и вероятностями P, – и определенная на этом пространстве
случайная величина Х. Эта случайная величина Х имеет определенную функцию распределения F(х) и соответствующие числовые характеристики.
Определите понятие « выборка из генеральной совокупности». В чем состоит репрезентативность выборки?
Выборкой объема n называется последовательность n независимых одинаково распределенных случайных величин Х1, Х2, …, Хn, распределение
каждой из которых совпадает с распределением исследуемой случайной величины X. Выборка – это результат n независимых последовательных наблюдений за случайной величиной Х из рассматриваемой генеральной совокупности. Результат наблюдений х1, х2, …, хn – одна из многих реализаций многомерной случайной величины Х1, Х2, …, Хn.
Для того, чтобы по выборке можно было сделать выводы об поведении интересующего нас признака генеральной совокупности , нужно, чтобы выборка правильно представляла особенности генеральной совокупности, то есть была репрезентативной(представительной). Из этого исходят свойства выборки:
Объём выборки достаточно большой;
Каждый объект выборки выбран случайно;
Для каждого объекта вероятность попасть в выборку одинакова.
3.Как строится вариационный ряд?
Пусть
интересующая нас случайная величина Х
принимает в выборке значение х1
п1
раз, х2
– п2
раз, …, хк
– пк
раз, причем
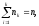 гдеп
– объем выборки. Тогда наблюдаемые
значения случайной величины х1,
х2,…,
хк
называют вариантами, а п1,
п2,…,
пк
– частотами. Если разделить каждую
частоту на объем выборки, то получим
относительные частоты
Последовательность
вариант, записанных в порядке возрастания,
называют вариационным рядом, а перечень
вариант и соответствующих им частот
или относительных частот – статистическим
рядом:
гдеп
– объем выборки. Тогда наблюдаемые
значения случайной величины х1,
х2,…,
хк
называют вариантами, а п1,
п2,…,
пк
– частотами. Если разделить каждую
частоту на объем выборки, то получим
относительные частоты
Последовательность
вариант, записанных в порядке возрастания,
называют вариационным рядом, а перечень
вариант и соответствующих им частот
или относительных частот – статистическим
рядом:
|
xi |
x1 |
x2 |
… |
xk |
|
ni |
n1 |
n2 |
… |
nk |
|
wi |
w1 |
w2 |
… |
wk |
Если объем выборки достаточно велик, то ее обработка оказывается громоздкой; в этом случае элементы выборки объединяют в группы. Для этого интервал [х(1), х(n)] разбивается на k равных интервалов. Количество
интервалов k в зависимости от объема выборки n обычно принимают от 8 до
20, или вычисляют по эмпирической формуле k = 1 + 3,32 lg n.
|
№ |
Границы интервала |
Середина
интервала( |
Частота ( |
Относи-тельная частота ( |
Накоплен- ная частота ( |
Накоплен-ная
относи-тельная частота- |
( w-длина интервала | |||||||
|
|
| |||||||||||||
|
1 |
… |
... |
… |
… |
… |
… |
… |
… | ||||||
|
k |
… |
… |
… |
… |
… |
… |
… |
… | ||||||
Далее
определяются частоты
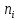 –
количество элементов выборки, попавших
в i-ый
интервал. Получающийся группированный
статистический ряд содержит середины
интервалов zi
и
частоты
–
количество элементов выборки, попавших
в i-ый
интервал. Получающийся группированный
статистический ряд содержит середины
интервалов zi
и
частоты
 (i
=
1, …, k).
Кроме того, подсчитываются накопленные
частоты , относительные частоты
(i
=
1, …, k).
Кроме того, подсчитываются накопленные
частоты , относительные частоты
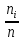 ,
накопленные относительные частоты
,
накопленные относительные частоты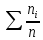 .
Таблица группированного статистического
ряда строится по данному виду:
.
Таблица группированного статистического
ряда строится по данному виду:

 )
) )
)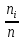 )
)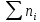 )
)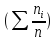
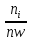 ),
),