Обработка результатов наблюдений, содержащих случайные погрешности

Среднее арифметическое значение

Повторив несколько наблюдений, получим ряд числовых значений измеряемой величины (Х₁, Х₂, ..., Х_n). Эти значения отличаются одно от другого, но если измерения проводились в одинаковых условиях и с одинаковой тщательностью, заслуживают одинакового доверия. Стремясь приблизиться к истинному значению измеряемой величины, вычисляют среднее арифметическое значение (или просто среднее) результатов ряда наблюдений по следующей формуле

 = (Х₁ + Х₂ + ... + Х_n)/n. (Пф.1)

Здесь  – среднее значение; Х_i – результат i-го наблюдения; n – число наблюдений.

При этом предполагается, что результаты наблюдений свободны от систематических погрешностей.

Отклонение от среднего

Отклонение от среднего V_i определяют по формуле

V_i = X_i - . (Пф.2)

Отклонения от среднего имеют два очень важных свойства, которые используются для контроля правильности вычислений:

1). Алгебраическая сумма отклонений от среднего равна нулю

V_i = 0. (Пф.3)

Это равенство справедливо всегда, если при вычислении среднего арифметического не производилось округление. Если же округление сделано, то всегда можно оценить, в какой степени отклонение от нуля соответствует этому округлению.

2). Сумма квадратов V_i имеет минимальное значение

V_i² = min. (Пф.4)

Если вместо среднего арифметического возьмем какое-либо другое значение и определим отклонение от него результатов отдельных наблюдений, то сумма квадратов этих отклонений всегда будет больше, чем сумма квадратов отклонений от среднего.

Определение среднего квадратического отклонения

по опытным данным

При бесконечном числе испытаний случайная величина может принимать любые значения, называемые генеральной совокупностью. Некоторое число n этих значений называют выборкой объема n. Определяя по данным этой выборки характеристики закона распределения, получаем не истинные значения дисперсии D, среднего квадратического отклонения  и т.д., характерные для всей генеральной совокупности, а лишь их оценки.

Оценка S среднего квадратического отклонения результата наблюдения (любого из ряда Х₁, Х₂, ..., Х_n) вычисляется по следующей формуле

S = . (Пф.5)

Появление в знаменателе подкоренного выражения (n-1) связано с заменой истинного значения измеряемой величины средним арифметическим результатов наблюдений.

Вычисление вероятности попадания случайной погрешности

в заданный интервал, уровень значимости

Вероятность попадания погрешности в доверительный интервал с границами +и -при нормальном распределении выражается формулой

Р[- <  < +] = Ф(t). (Пф.6)

Здесь функция Ф(t) (таблицы П.1, П.2) называется интегралом вероятностей (интегралом Лапласа); t = /; = t.

Вероятность того, что случайная погрешность окажется за границами интервала , равна P[  <  ] = 1-Ф(t). Ф(t), соответствующая данному доверительному интервалу , называется доверительной вероятностью, а значение 1-Ф(t) – уровнем значимости.

Доверительную вероятность выбирают в зависимости от конкретных условий. Часто пользуются доверительным интервалом от +3 до -3, для которого доверительная вероятность составляет 0.9973 или 99.73%.

Таблица П.1

Значения интеграла вероятностей

t	Ф(t)	t	Ф(t)	t	Ф(t)
0.00	0.0000	0.65	0.4843	1.25	0.7887
0.05	0.0399	0.70	0.5161	1.30	0.8064
0.10	0.0797	0.75	0.5467	1.35	0.8230
0.15	0.1192	0.80	0.5763	1.40	0.8385
0.20	0.1585	0.85	0.6047	1.45	0.8529
0.25	0.1974	0.90	0.6319	1.50	0.8664
0.30	0.2357	0.95	0.6579	1.55	0.8789
0.35	0.2737	1.00	0.6827	1.60	0.8904
0.40	0.3108	1.05	0.7063	1.65	0.9011
0.45	0.3473	1.10	0.7287	1.70	0.9109
0.50	0.3829	1.15	0.7499	1.75	0.9199
0.55	0.4177	1.20	0.7699	1.80	0.9281
0.60	0.4515

Пример 1. Известно, что среднее квадратическое отклонение равно  = 0.002. Определить вероятность того, что случайная погрешность измерения будет лежать в пределах доверительного интервала с границами  = 0.005 (0.5%).

Определяем t = /= 0.005/0.002 = 2.5. По таблице П.2 находим доверительную вероятность Ф(t), соответствующую t = 2.5, т.е. Ф(t) = 0.9876. Уровень значимости 1-Ф(t) = 0.0124.

Таблица П.2

Значения доверительной вероятности и уровня значимости

t	Ф(t)	1-Ф(t)	t	Ф(t)	1-Ф(t)
1.85	0.9357	0.0643	2.75	0.9940	6.0Е─3
1.90	0.9426	0.0574	2.80	0.9949	5.1Е─3
1.95	0.9488	0.0512	2.85	0.9956	4.4Е─3
2.00	0.9545	0.0455	2.90	0.9963	3.7Е─3
2.05	0.9596	0.0404	2.95	0.9968	3.2Е─3
2.10	0.9643	0.0357	3.00	0.9973	2.7Е─3
2.15	0.9684	0.0316	3.10	0.9981	1.9Е─3
2.20	0.9722	0.0278	3.20	0.9986	1.4Е─3
2.25	0.9756	0.0244	3.30	0.99904	9.6Е─4
2.30	0.9786	0.0214	3.40	0.99932	7.8Е─4
2.35	0.9812	0.0186	3.50	0.99954	4.6Е─4
2.40	0.9836	0.0174	3.60	0.99968	3.2Е─4
2.45	0.9857	0.0143	3.70	0.99978	2.2Е─4
2.50	0.9876	0.0124	3.80	0.99986	1.4Е─4
2.55	0.9892	0.0108	3.90	0.99990	1.0Е─4
2.60	0.9907	0.0093	4.00	0.999936	6.4Е─5
2.65	0.9920	0.0080	4.50	0.999994	6.0Е─6
2.70	0.9931	0.0069	5.00	0.9999994	6.0Е─7

Погрешности среднего арифметического

Если случайные погрешности результатов отдельных наблюдений подчиняются нормальному распределению, то и погрешности средних значений их повторных рядов подчиняются этому же закону, но с другим рассеянием. Рассеяние средних значений меньше, чем рассеяние результатов отдельных наблюдений.

Оценка S₀ среднего квадратического отклонения результата измерения (среднего, ) вычисляется по следующей формуле

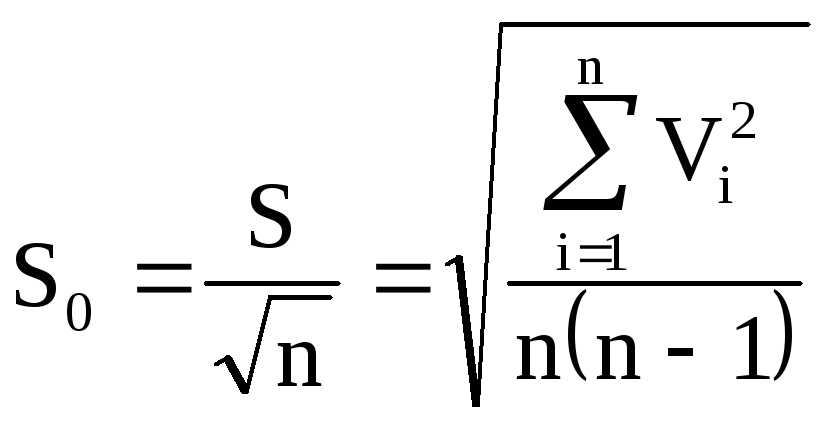. (Пф.7)

Доверительные интервалы и вероятности для среднего значения

То обстоятельство, что случайные погрешности среднего значения  также распределяются по нормальному закону, дает право определять для них доверительный интервал (Е) по формуле

. (Пф.8)

и пользоваться таблицами П.1-П.2.

Пример 2. Определить доверительный интервал для среднего значения из 64 наблюдений при S=0.04 и заданной доверительной вероятности 0.9.

Найдем среднее квадратическое отклонение среднего

S₀ = S /= 0.04 / = 0.005.

Для Ф(t) = 0.9 по таблице П.1 находим t = 1.645. Границы доверительного интервала: Е = tS₀ = 1.6450.005 0.008.

Оценка результатов при малом числе наблюдений

и неизвестной дисперсии

Рассмотренный выше способ определения доверительных интервалов справедлив только при большом количестве измерений (n>20-30). На практике значение Е приходится определять по результатам сравнительно небольшого числа измерений. При этом нужно пользоваться коэффициентами Стьюдента t_c, которые зависят от задаваемой доверительной вероятности P_c и числа измерений n (см. таблицу П.3, последняя строка дана для n ).

Таблица П.3

Коэффициенты Стьюдента t_c

n	Значения tc при Рc
	0.5	0.7	0.9	0.95	0.98	0.99	0.995	0.999
2	1.000	1.963	6.314	12.71	31.82	63.66	127.3	636.6
3	0.916	1.336	2.920	4.30	6.96	9.92	14.1	31.6
4	0.765	1.250	2.353	3.18	4.54	5.84	7.5	12.94
5	0.741	1.190	2.132	2.78	3.75	4.60	5.6	8.61
6	0.727	1.156	2.015	2.57	3.36	4.03	4.77	6.86
7	0.718	1.134	1.943	2.45	3.14	3.71	4.32	5.96
8	0.711	1.119	1.895	2.37	3.00	3.50	4.03	5.40
9	0.706	1.108	1.860	2.31	2.90	3.36	3.83	5.04
10	0.703	1.100	1.833	2.26	2.82	3.25	3.69	4.78
11	0.700	1.093	1.812	2.23	2.76	3.17	3.58	4.59
12	0.697	1.088	1.796	2.20	2.72	3.11	3.50	4.49
13	0.695	1.083	1.782	2.18	2.68	3.06	3.43	4.32
14	0.694	1.079	1.771	2.16	2.65	3.01	3.37	4.22
15	0.692	1.076	1.761	2.15	2.62	2.98	3.33	4.14
16	0.691	1.074	1.753	2.13	2.60	2.95	3.29	4.07
17	0.690	1.071	1.746	2.12	2.58	2.92	3.25	4.02
18	0.689	1.069	1.740	2.11	2.57	2.90	3.22	3.96
19	0.688	1.067	1.734	2.10	2.55	2.88	3.20	3.92
20	0.688	1.066	1.729	2.09	2.54	2.86	3.17	3.88
	0.674	1.036	1.645	1.96	2.33	2.58	2.81	3.29

При n   распределение Стьюдента сводится к нормальному. (Стьюдент - псевдоним английского статистика Уильяма Госсета).

В таблицах, приводимых в книгах по теории вероятностей, чаще указывается не число наблюдений n, а число степеней свободы k (k = n - 1).

Вместо доверительной вероятности Р_c в ряде книг указывается «Уровень значимости», равный 1-Р_c. Зная число наблюдений n и задавшись доверительной вероятностью Р_c, можно найти по таблице П.3 значение t_c, а умножив его на S₀ – определить границы доверительного интервала.

Пример 3. Шестикратное взвешивание изделия дало следующие результаты: 72.361; 72.357; 72.352; 72.346; 72.344; 72.340 г. Определить доверительный интервал для среднего при доверительной вероятности равной 0.99. Решение задачи представим в виде таблицы

Хi , г	Vi , мг	Vi2 , мг2
72.361	+ 11	121
72.357	+ 7	49
72.352	+ 2	4
72.346	- 4	16
72.344	- 6	36
72.340	-10	100
 = 72.350	Vi = 0	 Vi2 = 326

S = = = 8.1 мг; S₀ = S/ = 8.1/ = 3.3 мг.

По таблице П.3 находим для n = 6 и Р_c = 0.99 t_c = 4.03. Доверительный интервал для среднего (3.34.03) = 13 мг.

Оценка грубых результатов наблюдений

При обработке результатов наблюдений случайной величины, заведомо подчиняющейся нормальному закону распределения, при принятии решения об исключении или сохранении резко отличающихся результатов наблюдений (грубых) нужно внимательно проанализировать условия, в которых получился резко отличающийся результат. Сомнительным может быть лишь наибольший Х_max или наименьший X_min из результатов наблюдений. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами статистических гипотез.

Для проверки гипотезы, что результат не содержит грубой погрешности, вычисляют J_max = (X_max - )/S или J_min = ( - X_min)/S. Результаты J_max и J_min сравнивают с наибольшим значением J_p, которое случайная величина J может принимать по чисто случайным причинам.

Значения J_p для n = 315, при заданной доверительной вероятности, протабулированы и представлены в таблице П.4. Если вычисленное по опытным данным значение J окажется меньше J_p, то гипотеза принимается.

В противном случае результат Х_max или X_min приходится рассматривать как содержащий грубую погрешность и не принимать его во внимание при дальнейшей обработке результатов наблюдений.

Таблица П.4

Значения J_p

n	Значения Jp при Р равной
	0.9	0.95	0.975	0.99
3	1.406	1.412	1.414	1.414
4	1.645	1.689	1.710	1.723
5	1.731	1.869	1.917	1.955
6	1.894	1.996	2.067	2.130
7	1.974	2.093	2.182	2.265
8	2.041	2.172	2.273	2.374
9	2.097	2.237	2.349	2.464
10	2.146	2.294	2.414	2.540
11	2.190	2.383	2.470	2.606
12	2.229	2.387	2.519	2.663
13	2.264	2.426	2.562	2.714
14	2.297	2.461	2.602	2.759
15	2.326	2.493	2.638	2.808

Пример 4. Воспользуемся результатами наблюдений в приведенном выше примере 3. Определим, не содержит ли шестой результат (72.340 г) грубой погрешности, если принять доверительную вероятность Р = 0.975.

Из таблицы П.4 при n = 6 и Р = 0.975 находим J_p = 2.067. Поскольку J = ( - X_min)/S = (72.350 - 72.340)/0.0081 = 1.234, т.е. J < J_p, результат 72.340 не содержит грубую погрешность.

Оценка результатов неравноточных измерений

На практике не всегда можно обеспечить полную воспроизводимость условий повторных измерений. Случается так, что при проведении нескольких серий измерений некоторые из них оказываются менее надежными. Результаты этих наблюдений при обработке не следует отбрасывать. Они могут быть использованы (кроме, конечно, грубых погрешностей наблюдения). Их можно учесть, уменьшив в той или иной степени их роль, их «вес» в совокупности результатов всех измерений.

Понятие «вес» отражает степень доверия к результату измерения. Чем больше степень доверия к результату, тем больше его вес, тем больше число, выражающее этот вес. В этом случае значение измеряемой величины определяется по формуле

_o = (₁P₁" + ₂P₂" + ...+ _mP_m")/(P₁" + P₂" + ...+ P_m"). (Пф.9)

Здесь ₁, ₂, ..., _m – средние значения для отдельных групп измерений, полученные тем, или иным способом; Р₁", Р₂", ..., Р_m" – их вес; _o – среднее взвешенное значение.

Обозначение веса Р_i" тем же символом, что и вероятности (Р) не случайно. Наиболее правильным значением веса для данного результата является его вероятность. Если нет возможности определить вероятность, то числовые значения веса устанавливают, учитывая условия измерений. Рассмотрим некоторые из них (вес, в отличие от вероятности, обозначим Р").

Определение веса результата измерений

В основу вычислений могут быть взяты средние квадратические отклонения S_O. Веса соответствующих групп измерений считают обратно пропорциональными квадратам S_O, т.е.

P₁": P₂": ... : P_m" = 1/S_O1² : 1/S_O2² : ... : 1/S_Om².

Пример 5. Были проведены три группы измерений тремя наблюдателями. После обработки каждого ряда измерений были получены следующие результаты:

₁ = 20000.45; S_O1 = 0.05;

₂ = 20000.15; S_O2 = 0.20;

₃ = 20000.60; S_O3 = 0.10.

Определяем отношение весов:

Р₁" : Р₂" : Р₃" = 1/0.05² : 1/0.20² : 1/0.10² = 400 : 25 : 100 = 16 : 1 : 4.

В соответствии с этой пропорцией принимаем:

Р₁" = 16; Р₂" = 1; Р₃" = 4.

Находим среднее взвешенное значение

₀ = (1620000.45 + 120000.15 + 420000.60)/(16 + 1 + 4) = 20000.46.

Если среднее квадратическое отклонение в каждой группе S_oi одинаковы, т.е. S_oi = const, то критерием для определения весов результатов измерений нередко является число измерений n_i в каждой группе:

Р₁" : Р₂": ... : Р_m" = n₁ : n₂ : ... : n_m .

В данном случае среднее взвешенное будет равно среднему из всех измерений, рассматриваемых как один ряд

₀ = (₁n₁ + ₂n₂ + ... + _mn_m)/(n₁ + n₂ + ... + n_m).

Здесь n = n₁ + n₂ + ... + n_m – общее число наблюдений, проведенных во всех группах.