Внутренняя энергия трехмерной решетки Бравэ

В теории кристаллической решетки доказывается, что для трехмерной изотропной среды при заданном направлении волнового вектора решения уравнения движения можно выбрать таким образом, чтобы колебания ионов одной ветви нормальных мод были бы параллельны волновому вектору, а двух других ветвей - перпендикулярны. В первом случае мы имеем дело с продольной волной, а во втором - с поперечными, причем законы дисперсии всех трех волн будут различны. В общем случае, когда решетка Бравэ трехмерная, а число ионов в базисе равно p, имеется 3pN нормальных мод или 3p ветвей дисперсионной кривой. Из них три ветви акустические, а остальные 3(p-1) - оптические.

Таким образом, число нормальных мод моноатомного кристалла совпадает с числом степеней свободы образующих его ионов. Исходя из этого обстоятельства, Дебай предположил, что энергию колебаний следует приписать не отдельным ионам, а нормальным модам. Тогда внутреннюю энергию кристалла можно вычислять подобно тому, как ранее вычислялась энергия системы эйнштейновских осцилляторов (1.12)

. (1.42)

Разница заключается лишь в том, что теперь среднее число элементарных возбуждений данной моды , как и их энергия, зависят от волнового вектора, поэтому для вычисления внутренней энергии необходимо просуммировать (1.42) по всемиs:

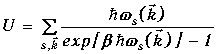. (1.43)

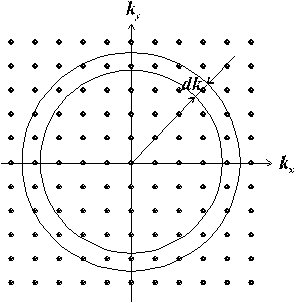
Рис. 1.7

Изображение нормальных мод в виде точек k-пространства.

Предположим для простоты, что кристалл, внутреннюю энергию которого необходимо вычислить, имеет простую кубическую решетку с периодом a и форму параллелепипеда со сторонами . Соответственно, первая зона Бриллюэна будет иметь форму куба со стороной. Если нормальные моды рассматриваемой решетки изображать при помощи соответствующих волновых векторов, а точнее - при помощи точек, в которые упираются концы этих векторов, то мы получим картину подобную той, что изображена на рисунке 1.7. При этом расстояние между точками в направлении осейx, y и z будет равно ,и, соответственно. При характерных размерах кристалла порядкарасстояние между двумя точками (состояниями) будет величиной порядка, что пренебрежимо мало по сравнению с размерами зоны Бриллюэна, имеющими порядок. Другими словами, суммирование в (1.43) можно заменить интегрированием по первой зоне Бриллюэна

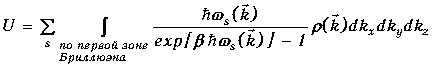, (1.44)

где - плотность изображающих точек или плотность состояний. В данном случае плотность состояний - величина постоянная, и ее можно найти как величину обратную объемуk-пространства, приходящемуся на одно состояние

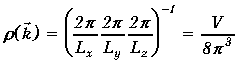, (1.45)

где V - объем кристалла.

Для вычисления интеграла (1.44) необходимо знать зависимость частоты от волнового вектора, которая нам неизвестна. Поэтому Дебай предложил использовать при расчете простую интерполяционную схему, согласно которой закон дисперсии полагается линейным и одинаковым для всех трех кристаллографических направлений трех ветвей дисперсионной кривой

. (1.46)

Здесь фазовая скорость одновременно играет роль подгоночного параметра. Тогда с учетом (1.45) и (1.46) выражение (1.44) можно переписать в виде

. (1.47)

Теперь, когда под интегралом в (1.47) стоит функция модуля волнового вектора, нет смысла вычислять тройной интеграл по первой зоне Бриллюэна. Очевидно, что в рамках схемы Дебая изоэнергетической поверхностью в k-пространстве будет сфера (рис. 1.7). Поэтому целесообразно перейти к сферическим координатам, а число состояний в элементарном объеме вычислять как отношение элементарного объема к объему одного состояния. Однако при этом возникают проблемы с пределами интегрирования, для устранения которых Дебай предложил заменить интегрирование по первой зоне Бриллюэна интегралом по сфере радиуса, содержащей столько же состояний, что и зона Бриллюэна.

Учитывая сделанные выше допущения и принимая во внимание, что , выражение (1.47) можно переписать в виде

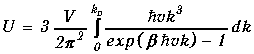. (1.48)

Радиус сферы Дебая найдем, приравняв произведение объема сферы Дебая на плотность состояний к числу состояний

(1.49)

откуда

, (1.50)

где - концентрация ионов кристаллической решетки.

В (1.48) введем новую переменную

, (1.51)

где

. (1.52)

Параметры с индексом "D" в (1.52) получили название частоты Дебая, энергии Дебая и температуры Дебая. С учетом соотношения комплекс параметров перед интегралом (1.51) преобразуем к виду

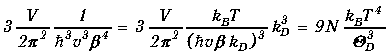(1.53)

и, заменив верхний предел интегрирования в соответствии с (1.52), получим

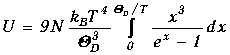. (1.54)

Теплоемкость кристалла найдем как производную (1.54) по температуре

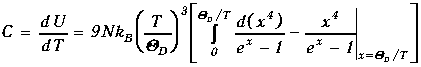. (1.55)

Вычисляя интеграл в (1.55) по частям и принимая во внимание, что , находим

. (1.56)

Подставив (1.56) в (1.55) и положив , получим окончательное выражение для молярной теплоемкости кристаллического диэлектрика

. (1.57)

Функция (1.57) относится к числу специальных функций и ее численные значения приведены в соответствующих справочниках.

Необходимо помнить, что выражение (1.57) - лишь результат интерполяции, который хорошо согласуется с экспериментом только при соответствующем выборе подгоночного параметра. Этим параметром первоначально была скорость v, одинаковая для всех ветвей закона дисперсии, которая при замене переменных вошла в температуру Дебая. Таким образом, температура Дебая, к которой перешла роль подгоночного параметра, должна выбираться так, чтобы зависимость (1.57) наилучшим образом согласовывалась с результатами эксперимента во всем интервале температур.