Нормальные моды одномерной решетки с базисом.

Рассмотрим одномерную решетку Бравэ с двумя ионами в элементарной ячейке. Пусть равновесные положения ионов (рис. 1.5) находятся в точках na и na + l. Будем считать, что ионы идентичны и взаимодействуют лишь c ближайшими соседями. Тогда жесткость связи G между ионами, находящимися на расстоянии a - l, будет меньше, чем жесткость K связи между ионами, отстоящими на расстояние l, поскольку a - l > l. Отклонение ионов, находящихся в узлах na от

Рис. 1.5

Одномерная решетка Бравэ с базисом

положения равновесия, обозначим как , а отклонение ионов от узловna + l обозначим через . Потенциальная энергия взаимодействия всей цепочки ионов будет равна

. (1.34)

Уравнения движения для ионов в ячейке na имеют вид

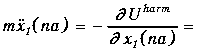
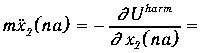
(1.35)

с периодическим граничным условием (1.26).

Решения уравнений (1.35) ищем в виде

,(1.36)

где и- комплексные амплитуды колебаний. Подставляя (1.36) в (1.35) приходим к следующей системе уравнений относительно комплексных амплитуд

.(1.37)

Условием ненулевых решений системы (1.37) будет равенство нулю ее детерминанта, раскрыв который приходим к следующему квадратному уравнению

. (1.38)

Преобразуя квадрат модуля и извлекая квадратный корень, найдем закон дисперсии нормальных мод

. (1.39)

Поделив почленно уравнения (1.37), несложно получить следующее соотношение

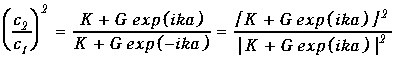. (1.40)

Извлекая квадратный корень из (1.40), приходим к следующему соотношению между комплексными амплитудами колебаний

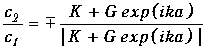(1.41)

Как следует из (1.39), для каждого из N значений волнового вектора имеется два значения частоты или две нормальные моды, а в целом число нормальных мод составляет 2N. Изображая нормальные моды с помощью дисперсионных кривых в первой зоне Бриллюэна, мы получим две зависимости , о которых обычно говорят как о двух ветвях закона дисперсии. Нижняя ветвь дисперсионной кривой, показанной на рис. 1.6, соответствует волнам того же типа, что и в моноатомной решетке Бравэ. В области длинных волны частота линейно зависит от волнового числа, а фазовая и групповая скорости совпадают. Такой закон дисперсии характерен для звуковых волн, поэтому нижнюю ветвь называют акустической. На границе зоны Бриллюэна акустическая ветвь параллельна оси абсцисс, а. Очевидно, что в этом случае групповая скорость волн акустической ветви равна нулю, тогда как фазовая скорость составляет. Верхняя ветвь дисперсионной кривой начинается в точкеи, опускаясь с ростом волнового числа, достигает значенияна краю зоны Бриллюэна. Соответственно, групповая скорость обращается в ноль в центре и на границах зоны, тогда фазовая скорость изменяется от бесконечности до.

Рис. 1.6

Закон дисперсии нормальных мод одномерной решетки с базисом

Чтобы лучше понять, каким волновым движениям соответствует вторая ветвь дисперсионной кривой, исследуем соотношение (1.41). Последнее представляет собой отношение комплексных амплитуд, включающих помимо собственно амплитуды также и фазу колебаний. При имеем, где нижний знак соответствует акустической ветви - такому движению, при котором фазы двух ионов в одной ячейке одинаковы, т.е. оба иона движутся в одну сторону. Верхнему знаку отвечает верхняя ветвь дисперсионной кривой, когда ионы движутся в противофазе, т.е. в противоположные стороны. Подобным образом колеблются ионы изолированной молекулы, когда сохраняется импульс, но изменяется дипольный момент. Такая колебательная мода может взаимодействовать с электромагнитным излучением, поэтому ее называют оптической.

При имеем, что означает изменение фазы колебаний на противоположную. Теперь оптической ветви дисперсионной кривой соответствуют синфазные движения ионов одной ячейки, а акустической ветви - движения в противофазе. Но при этом фазы колебаний ионов соседних ячеек сдвинуты на, в результате чего на границе зоны Бриллюэна деформируются связи только одного типа:K - в оптической ветви и G - в акустической ветви.