Модель Эйнштейна
Закон Дюлонга и
Пти находится в хорошем соответствии
с экспериментальными данными в области
температур выше комнатной и нарушается
при низких температурах, когда теплоемкость
кристалла падает по закону
(см.
рис.1.1). Чтобы привести модель независимых
осцилляторов в соответствие с
экспериментальными данными, Эйнштейн
в 1907 году предложил использовать
Рис. 1.1
Температурная зависимость теплоемкости серебра
представление о
квантовых осцилляторах. В отличие от
более ранней механической модели
предполагалось, что энергия колебаний
ионов изменяется конечными порциями
(квантами) равными
и
может принимать только значения из ряда
,
(1.9)
где
-
постоянная Планка. Среднее значение
энергии отдельного осциллятора
вычисляется как среднее значение
случайной величины
.
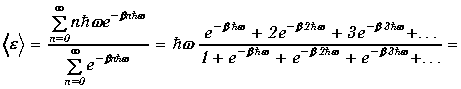
(1.10)
Выражение под
логарифмом представляет собой сумму
членов геометрической прогрессии со
знаменателем
.
Воспользовавшись известной формулой
,
несложно вычислить среднее значение энергии осциллятора
.
(1.11)
Этот результат обычно записывается в виде
,
(1.12)
и интерпретируется
следующим образом: среднее
значение энергии осциллятора есть
произведение энергии элементарного
возбуждения
на
среднее число элементарных возбуждений
.
(1.13)
Внутреннюю энергию одного моля можно выразить как произведение средней энергии осциллятора на число Авогадро и число степеней свободы
.
(1.14)
Дифференцируя (1.14) по T, получим молярную теплоемкость кристалла
.
(1.15)
Очевидно, что
выражение (1.15) при высоких температурах
должно переходить в закон Дюлонга и
Пти, поскольку дискретность энергетических
состояний осцилляторов при высоких
температурах не играет существенной
роли. Напротив, при низких температурах
квантовые свойства системы играют
определяющую роль, и температурная
зависимость теплоемкости должна
отклоняться от закона
.
Таким образом, существует некоторая
характеристическая температура, ниже
которой осцилляторы проявляют квантовые
свойства, а выше - ведут себя как
классические осцилляторы. Эта температура
называетсятемпературой
Эйнштейна
и
вводится при помощи соотношения
.
(1.16)
Подставляя (1.16) в (1.15) получим выражение
,
(1.17)
более удобное, нежели (1.15) для исследования асимптотического поведения теплоемкости, к которому мы и переходим.
Первоначально
рассмотрим область высоких температур
,
где температура Эйнштейна величина
порядка
.
В этом случае показатель экспоненты в
соотношении (1.11), которое с учетом (1.16)
принимает вид
,
(1.18)
много меньше единицы и экспоненту можно разложить в ряд, ограничившись линейным членом
.
(1.19)
Тогда выражение для молярной теплоемкости в пределе высоких температур будет стремиться к закону Дюлонга и Пти
.
(1.20)
При низких
температурах
,
когда в знаменателе (1.17) можно пренебречь
единицей по отношению к экспоненте,
имеем экспоненциальную зависимость
теплоемкости от температуры
.
(1.21)
Как видно графиков, представленных на рис. 1.2 теплоемкость по Эйнштейну весьма близка к реальности. Тем не менее в области низких температур модель
Рис. 1.2
Сравнение теплоемкости по Эйнштейну (кривая 2) с экспериментальной температурной зависимостью теплоемкости серебра (кривая 1).
Эйнштейна предсказывает экспоненциальное убывание теплоемкости (1.21), тогда как из эксперимента следовало, что теплоемкость спадает по кубическому закону.