Курсовые / Свойства суспензии сферических магнитных частиц

Московский институт электронной техники.

(Технический Университет)

Кафедра КФН.

Голохов М.Г.

Курсовая работа

по курсу:

Квантовая теория и

статистическая физика.

Москва 2004 г.

Введение.

В данной курсовой работе мы рассмотрим электропроводную ньютоновскую жидкость, в которой взвешено большее количество твердых сферических однородно намагниченных частиц. Мы также установим, что в гидродинамическом отношении суспензия сферических магнитных частиц в электропроводной жидкости в отсутствие внешних полей подобна суспензии эллипсоидов вращения в обычной жидкости.

Эффективная вязкость суспензии магнитных частиц в

электропроводной жидкости.

Для начала вычислим эффективную вязкость суспензии твердых шариков. Жидкость, в которой взвешено большое количество мелких твердых частиц (суспензия), можно рассматривать как однородную среду, если мы интересуемся явлениями, характеризующимися расстояниями, большими по сравнению с размерами частиц. Такая среда будет обладать эффективной вязкостью , отличной от вязкости основной жидкости. Эта вязкость может быть вычислена для случая малых концентраций взвешенных частиц (т.е. суммарный объем всех частиц предполагается малым по сравнению с объемом всей жидкости). Вычисления сравнительно просты для случая шарообразных частиц.

В качестве вспомогательной задачи необходимо предварительно рассмотреть влияние, которое оказывает один погруженный в жидкость твердый шарик на течение, обладающее постоянным градиентом скорости. Пусть невозмущенное шариком течение описывается линейным распределением скоростей

, (1)

где – постоянный симметрический тензор. Давление в жидкости при этом постоянно: ; условимся в дальнейшем отсчитывать давление от этого постоянного значения. В силу несжимаемости жидкости () тензор должен иметь равной нулю след:

. (2)

Пусть теперь в начало координат помещен шарик радиуса . Скорость измененного им течения обозначим посредством ; на бесконечности должно обращаться в нуль, но вблизи шарика отнюдь не мало по сравнению с . Из симметрии течения ясно, что шарик останется неподвижным, так что граничное условие гласит: при .

Рассмотрим уравнение Навье-Стокса для движений с малым числом Рейнольдса. Для стационарного движения несжимаемой жидкости это уравнение имеет вид

.

Член имеет порядок величины . Выражение же . Отношение первой величины ко второй есть как раз число Рейнольдса. Поэтому при членом можно пренебречь, и уравнение движения сводится к линейному уравнению

. (3)

Вместе с уравнением непрерывности

(4)

оно полностью определяет движение. Полезно также заметить уравнение

, (5)

получающееся применением операции к уравнению (3)

Рассмотрим прямолинейное и равномерное движение шара в вязкой жидкости. Эта задача вполне эквивалентна задаче об обтекании шара потоком жидкости, имеющим на бесконечность заданную скорость . Распределение скоростей в первой задаче получается из решения второй задачи просто вычитанием скорости ; тогда жидкость на бесконечности оказывается неподвижной, а шар движется со скоростью – . Если мы рассматриваем движение как стационарное, то надо, конечно, говорить именно об обтекании жидкостью неподвижного шара, так как при движущемся шаре скорость жидкости в каждой точке пространства меняется со временем.

Поскольку , то может быть представлена в виде ротора некоторого вектора :

,

причем обращается на бесконечность в нуль. Вектор должен быть аксиальным для того, чтобы его ротор был полярным вектором, как скорость. В задаче об обтекании полностью симметричного тела–шара–нет никаких выделенных направлений за исключением направления . Этот параметр должен входить в линейно – в виду линейности уравнения движения и граничных условий к нему. Общий вид векторной функции , удовлетворяющей всем этим требованиям, есть , где – единичный вектор в направлении радиус-вектора (начало координат выбираем в центре шара), а – скалярная функция от . Произведение можно представить в виде градиента некоторой другой функции . Таким образом, получаем

, (6)

где , , .

Искомое решение уравнений движения (3)-(5) может быть получено непосредственно из найденного решения (6), если заметить, что производные от последнего по координатам тоже являются решениями. В данном случае мы ищем решение, зависящее как от параметров от компонент тензора (а не от вектора ). Таковым является

,

где () обозначает вектор с компонентами . Раскрывая эти выражения и выбирая постоянные и в функции так, чтобы удовлетворить граничным условиям на поверхности шарика, получим в результате следующие формулы для скорости и давления:

, (7)

(8)

(– единичный вектор в направлении радиус-вектора).

Переходя теперь к самому вопросу об определении эффективной вязкости суспензии, вычислим среднее (по всему объему) значение тензора плотности потока импульса , совпадающего в линейном по скорости приближении с тензором напряжений – :

.

Интегрирование можно производить здесь по объему сферы большего радиуса, который затем устремляется к бесконечности.

Прежде всего, пишем тождественно:

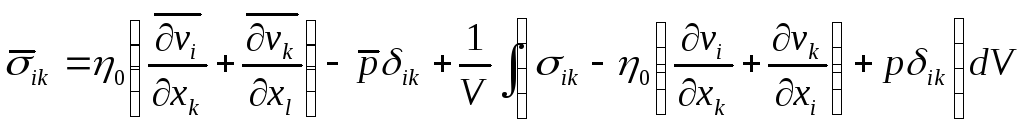. (9)

В стоящем здесь интеграле подынтегральное выражение отлично от нуля лишь внутри твердых шариков; ввиду предполагаемой малости концентрации суспензии его можно вычислять для одного отдельного шарика, как если бы других вообще не было, после чего результат должен быть умножен на концентрацию суспензии (число шариков в единице объема). Непосредственное вычисление такого интеграла требовало бы исследование внутренних напряжений в шариках. Можно, однако, обойти это затруднение путем преобразования интеграла по объему в интеграл по поверхности бесконечно удаленной сферы, проходящей только через жидкость. Для этого замечаем, что ввиду уравнения движения имеет место тождество

;

поэтому преобразование объемного интеграла в поверхностный дает

.

Член с мы опустили, имея в виду, что среднее давление непременно обращается в нуль (действительно, это есть скаляр, который должен определяться линейной комбинацией компонент тензора ; но единственный такой скаляр ).

При вычислении интеграла по сфере очень большого радиуса в выражении (7) для скорости следует, конечно, сохранить лишь члены ~. Простое вычисление дает для этого интеграла

,

где черта обозначает усреднение по направлениям единичного вектора . Искомые средние значения произведений компонент единичного вектора представляют собой симметричные тензоры, которые могут быть составлены только из единичных тензоров . Имея это в виду, легко найти, что

, .

Производя усреднение, получаем окончательно:

. (10)

Первое слагаемое в (10) после подстановки в него из (1) дает ; член же первого порядка малости в этом слагаемом тождественно обращается в ноль после усреднения по направлениям (как и должно было быть, поскольку весь эффект заключен в выделенном в (9) интеграле). Поэтому искомая относительная поправка в эффективной вязкости суспензии определяется отношением второго члена в (10) к первому. Таким образом, получим

, , (11)

где – малое отношение суммарного объема всех шариков к полному объему суспензии.

Уже для суспензии с частицами в виде эллипсоидов вращения и окончательные формулы становятся очень громоздкими. В потоке суспензии с нешарообразными частицами наличие градиентов скорости оказывает ориентирующее действие на частицы. Под влиянием одновременного воздействия ориентирующих гидродинамических сил и дезориентирующего вращательного броуновского движения устанавливается анизотропное распределение частиц по их ориентации в пространстве. Этот эффект, однако, не должен учитываться при вычислении поправки к вязкости : анизотропия ориентационного распределения сама зависит от градиентов скорости (в первом приближении – линейно) и ее учет привел бы к появлению в тензоре напряжений нелинейных по градиентам членов.

Представляет интерес изучить этот вопрос для суспензии магнитных частиц в электропроводной жидкости. Хотя в отсутствии внешних полей такая суспензия не обладает макроскопической намагниченностью и в ней нет макроскопических токов проводимости, локальные магнитные поля частиц и индуцируемые ими в окрестности частиц токи придают задаче большое своеобразие.

Рассмотрим электропроводную ньютоновскую жидкость* [см. стр. 11], в которой взвешено большое количество твердых сферических однородно намагниченных частиц. Вычислим эффективную вязкость и тензор вязких напряжений такой среды, следуя программе энергетического метода. Покажем, что в гидродинамическом отношении суспензия сферических намагниченных частиц в электропроводной жидкости подобна суспензии эллипсоидов вращения в обычной жидкости.

Отправной точкой энергетического метода является исследование магнитной гидродинамики в окрестности уединенной частицы, помещенной в потенциальный поток

. (12)

Здесь – постоянный тензор** [см. стр. 11] скорости деформации невозмущенного частицей течения. В случае чисто вязкого обтекания для скорости и давления найдено:

,

. (13)

Здесь – радиус частицы, – расстояние от начала координат, где помещена частица, – вязкость несущей жидкости. Расчет дополнительных возмущений, вносимых МГД-эффектами. В приближении малых значений чисел Гартмана, Рейнольдса и магнитного числа Рейнольдса для поправок давления , скорости , электрических потенциалов индуцированного поля в жидкости () и в частице () найдено:

,

, (14)

.

Здесь – величина магнитного момента частицы и – его орт, – коэффициенты электропроводимости жидкости () и частицы (), – скорость света.

Энергию, диссипируемую в единице объема суспензии за единицу времени, вычислим как произведение числа частиц в единице объема на вклад отдельной частицы:

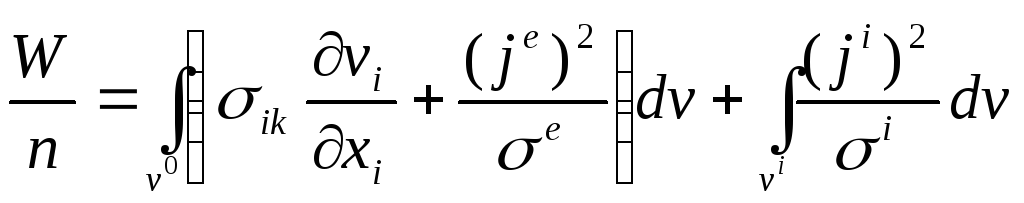. (15)

Здесь первый интеграл вычисляется по объему жидкости, а второй – частицы; далее

–

тензор напряжений в жидкости,

, () – (16)

плотность тока проводимости в жидкости и частице, – напряженность магнитного поля в жидкости. Отметим, что плотность тока в (16) определяется по чисто вязкому профилю скорости (13) и невозмущенной напряженности поля , . Учитывая уравнения движения

, ,

имеем

.

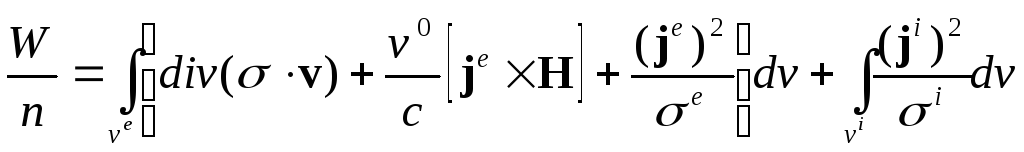Используя (16) и закон сохранения заряда , запишем

,

.

Тогда в первом приближении по возмущению

. (17)

Здесь – чисто вязкий вклад. Переходя в (17) к интегралам по поверхности и учитывая непрерывность на поверхности частицы электрического потенциала и нормальной компоненты тока, имеем

(18)

Здесь – внешняя поверхность объема , – нормаль к ней. При интегрировании по бесконечно удаленной поверхности сохранится вклад слагаемых в подынтегральном выражении, уменьшающихся с расстоянием как. Используя соотношения (13), (14), (16), найдем, что вклад электромагнитного слагаемого обращается в нуль, а в разложениях по степеням ненулевой вклад дадут члены разложения

;

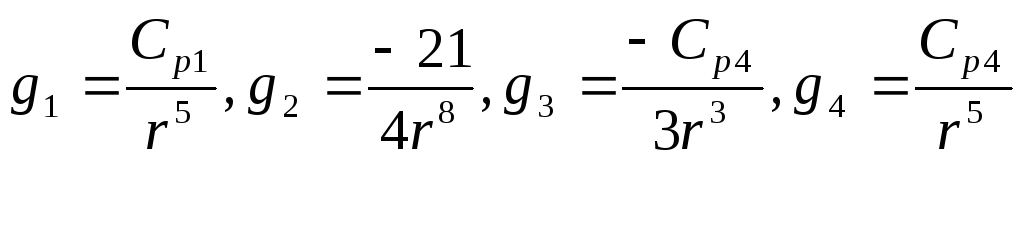; (19)

,

.

В результате интегрирования находим выражение через тензор скорости деформации невозмущенного течения

(20)

Здесь

, ,

;

,

, .

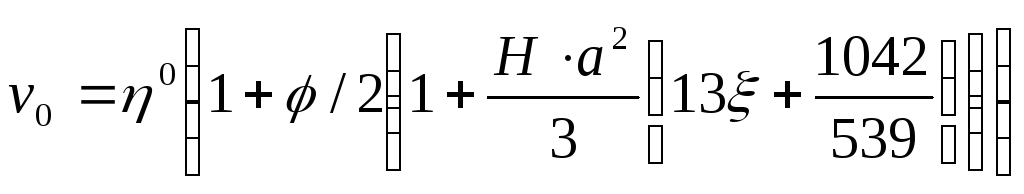Средний тензор скорости вычисляется путем усреднения локального значения тензора скорости сдвига

,

по объему, содержащему большое число частиц. Окончательный результат вычислений, следующий:

. (21)

Здесь

,

. (22)

, .

Эффективная вязкость суспензии есть тензор четвертого ранга в выражении мощности диссипации через средний тензор скорости сдвига:

. (23)

Соотношение (23) можно получить из соотношения (10), подставив в него выражение для тензора скорости деформации невозмущенного течения через усредненный тензор деформации , разрешив уравнение (21) относительно :

. (24)