§2.3. Системы линейных уравнений.

Общий вид СЛУ задается системой:

(*)

Набор чисел такой, который при подстановке вместо, каждое из уравнений системы обращает в тождество, называется еечастным решением. Найти общее решение СЛУ, значит указать метод, позволяющий получить все частные ее решения. СЛУ называется совместной, если она имеет хотя бы одно частное решение, и несовместной– иначе.

Классической является следующая

ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ. Система линейных уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу расширенной.

ДОКАЗАТЕЛЬСТВО. Пусть СЛУ (*) имеет частное решение . Видно, что столбец из свободных членов СЛУ является линейной комбинацией столбцов ее основной матрицы. Поэтому ранг основной матрицы равен рангу расширенной.

Обратно, пусть ранг основной матрицы СЛУ равен рангу расширенной. С точностью до перестановки уравнений и переименования неизвестных можно считать, что минор наивысшего порядка r находится на пересечении первых r строк и столбцов основной матрицы. Следовательно, существуют такие числа , что столбец из свободных членов равен линейной комбинации первыхстолбцов основной матрицы. Полагая, видно, что() является решением СЛУ (*). □

Две СЛУ от одного и того же числа неизвестных называются равносильными, если они обе не совместны, либо множества их частных решений равны. Нетрудно показать, что полученная СЛУ равносильна исходной, если

• из СЛУ вычеркнуть уравнение вида ;

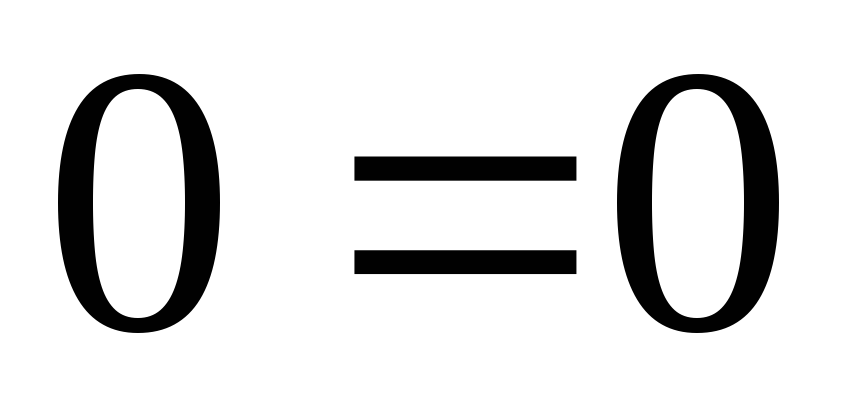• обе части какого-то уравнения СЛУ умножить на число, отличное от нуля;

• прибавить к одному из уравнений другое, умноженное на некоторое число.

Изложим один метод решения СЛУ (*), называемый методом последовательного исключения переменных (или методом Гаусса). Будем считать, что (этого можно всегда добиться с помощью перестановок строк). Попытаемся теперь, умножая первое уравнение на подходящие числа и прибавляя его к последующим, уничтожить в них слагаемые, содержащие. Для этого, умножаем первое уравнение наи прибавляем ко второму, и так далее, пока не умножим первое уравнение наи не прибавим к последнему. Получим равносильную СЛУ вида

Полагаем, что (этого можно добиться, переставляя строки или переименовывая переменные). Затем временно «забываем» про первое уравнение и продолжаем такую процедуру с оставшимися. Если в результате этой процедуры возникнет уравнение видаи, то система несовместна, если же одно из уравнений окажется вида, то это уравнение можно опустить. В результата придем к ступенчатой СЛУ, которая имеет вид

Эта часть метода Гаусса часто носит название «прямого хода». Заметим, что число является рангом основной матрицы СЛУ и он равен рангу расширенной. Теперь для нахождения общего решения СЛУ (*) воспользуемся «обратным ходом». Для этого из последнего уравнения системы выразимчерез. Зная это выражение из предпоследнего уравнения можно выразитьтакже через, и так далее. Наконец получим систему

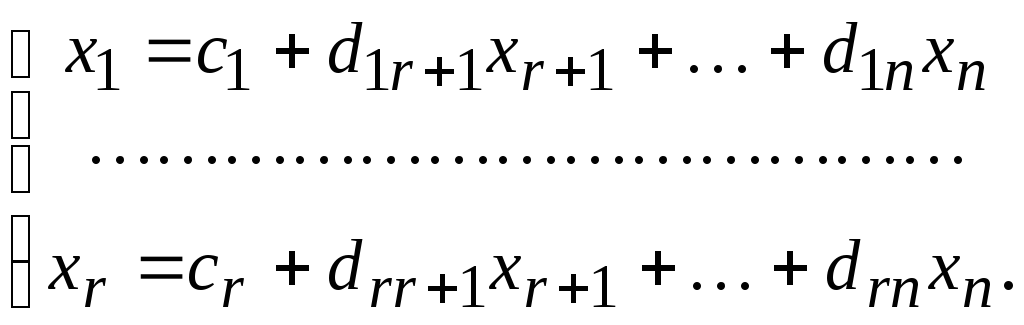
Она равносильна исходной и называется общим решением СЛУ (*). Теперь подставляя вместо неизвестных произвольные значения и вычисляяможно получить все частные решения () СЛУ (*).

Пример 3. Решить систему уравнений

Решение. Подвергнем преобразованиям расширенную матрицу этой системы:

Ранг основной матрицы системы равен рангу расширенной матрицы и равен двум. Приходим, следовательно, к системе уравнений, равносильной исходной

,

в которой одна переменная является независимой. В качестве независимой переменной возьмём , и выразим через неё остальные, получим:

.

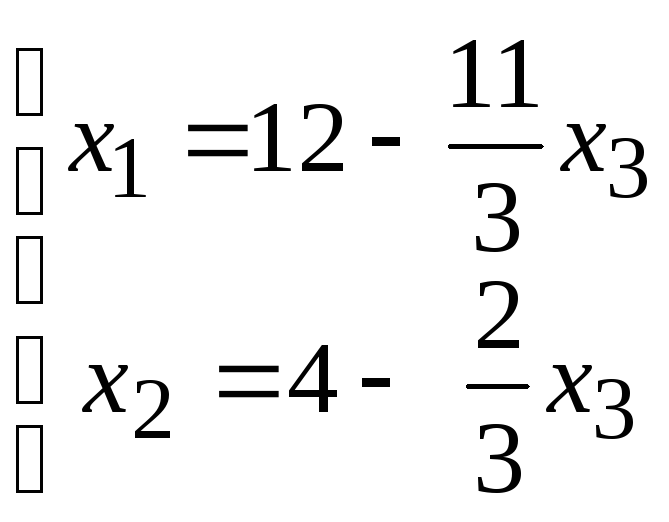Полагая, например, , получим одно из частных решений системы:

Если все свободные члены СЛУ равны, то СЛУ называется системой линейных однородных уравнений (СЛОУ). СЛОУ всегда имеет тривиальное (нулевое) решение . Несложно проверить истинность следующих утверждений:

• сумма двух частных решений СЛОУ также является ее частным решением;

• если число умножить на частное решение СЛОУ, то получится также ее частное решение.

В частности, если СЛОУ зависит от n неизвестных, то множество всех частных решений ее образует подпространство в пространстве . Базис этого подпространства называетсяфундаментальной системой решений СЛОУ.

ТЕОРЕМА (о СЛОУ). Фундаментальная система решений СЛОУ состоит из некоторых ее частных решений, гдечисло неизвестных СЛОУ, аранг ее основной матрицы.

ДОКАЗАТЕЛЬСТВО. Рассмотрим СЛОУ (*), считая, что . Найдем ее общее решение, которое будет иметь вид

Далее свободным неизвестным будем приписывать последовательно, а всем остальным. Получим частных решений, которые сведем в следующую таблицу

				1	0		0
				0	1		0
				0	0		1

Покажем, что векторы

образуют фундаментальную систему СЛОУ (*).

Минор, стоящий на пересечении всех ее решений и последних их столбцов не равен . Значит, решения линейно независимы. Пусть теперькакое-то ее частное решение. Докажем, что векторлинейно выражается через векторы. Рассмотрим линейную комбинацию, вектортоже является решением СЛОУ. Имеем,. Ноиоднозначно определяются в общем решении через значения, придаваемых свободным неизвестным. Поэтому. Таким образом, векторыявляются и системой порождающих подпространства решений СЛОУ, т.е. ее базисом. □

СЛЕДСТВИЕ. СЛОУ имеет тривиальное решение в том и только в том случае, когда ранг ее основной матрицы равен числу неизвестных. □

Таблица, приведенная выше, позволяет практически находить фундаментальную систему решений СЛОУ, чем должно заканчиваться ее решение.

Пример 4. Решить систему

Решение. Это система однородных уравнений, причём число уравнений меньше числа неизвестных; она будет иметь множество решений. Так как все свободные члены равны нулю, то будем подвергать преобразованиям лишь матрицу из коэффициентов системы:

Мы пришли к системе уравнений

В качестве независимых выберем две переменные, например . Выразим остальные переменные через независимые. Получим

Тогда фундаментальная система будет иметь следующий вид:

-8	-5	1	0
19	11	0	1

Любое частное решение системы может быть представлено в виде линейной комбинации фундаментальных решений, т. е. общее решение системы

ЗАДАЧИ К ГЛАВЕ II.

Найти ранг следующих матриц методом окаймления миноров:

78.

79.

80.

Вычислить ранг следующих матриц при помощи элементарных преобразований:

81.

82.

83.

84.

85.

86.

Определить ранг матриц при различных значениях :

87.

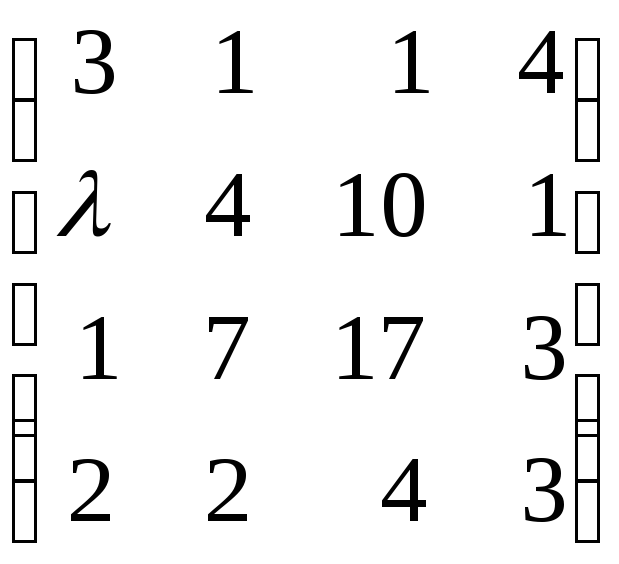
88.

Исследовать совместность и найти общее и одно частное решение системы уравнений:

89.

90.

91.

92.

93.

94.

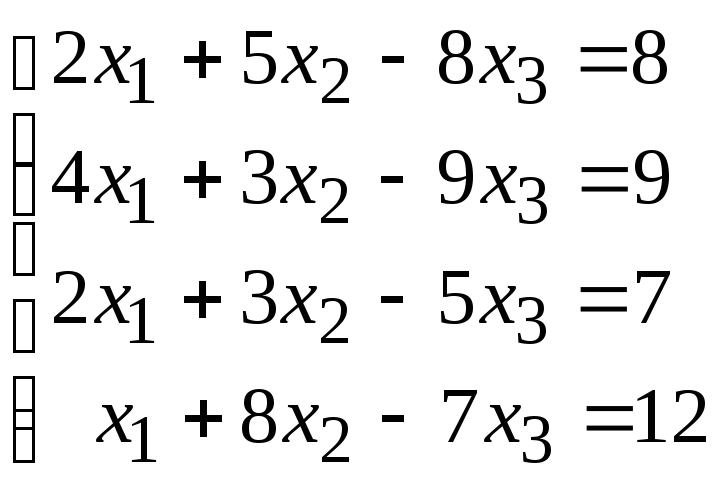
95.

96.

97.

98.

99.

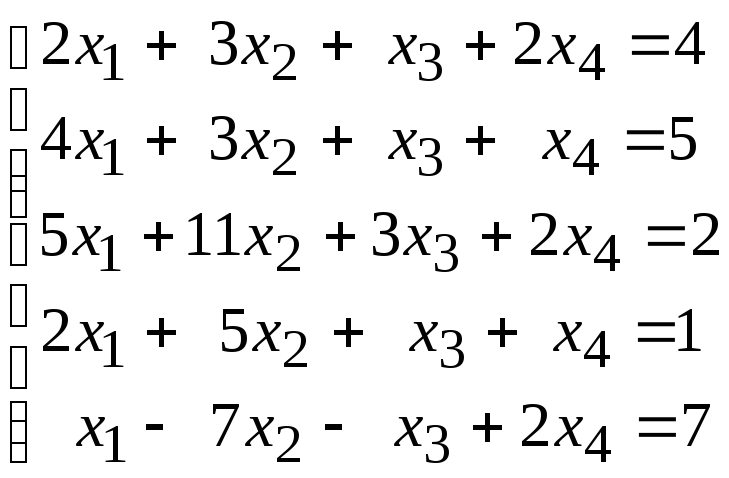
Исследовать систему и найти общее решение в зависимости от значений параметра :

100.

101.

Найти общее решение и фундаментальную систему решений для систем уравнений:

102.

103.

104.

105.

106.

107.

108.

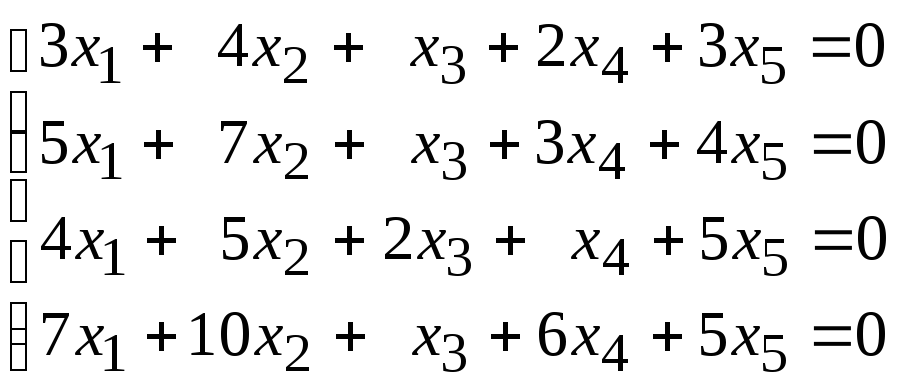
109. Какие из строк матрицы

образуют фундаментальную систему решений для системы уравнений