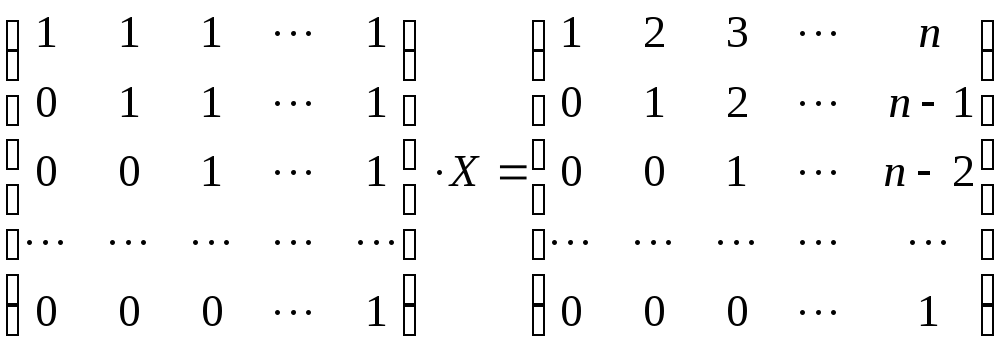§1.3. Теоремы о произведении определителей и обратной матрице. Правило Крамера.

ТЕОРЕМА (о произведении определителей). Определитель произведения двух квадратных матриц иодного и того же порядка _{равен произведению их определителей, т.е.}

ДОКАЗАТЕЛЬСТВО. Рассмотрим вспомогательный определитель порядка

Используя теорему Лапласа, вычислим ,разлагая его по первым строкам. Так как в них лишь один минор может быть не равен , а его алгебраическое дополнение есть, то . Используя свойство 9 определителей, добьемся, что все элементы обратились в. Для этогостолбец умножим на и прибавим кстолбцу , и так для каждых и. Получим

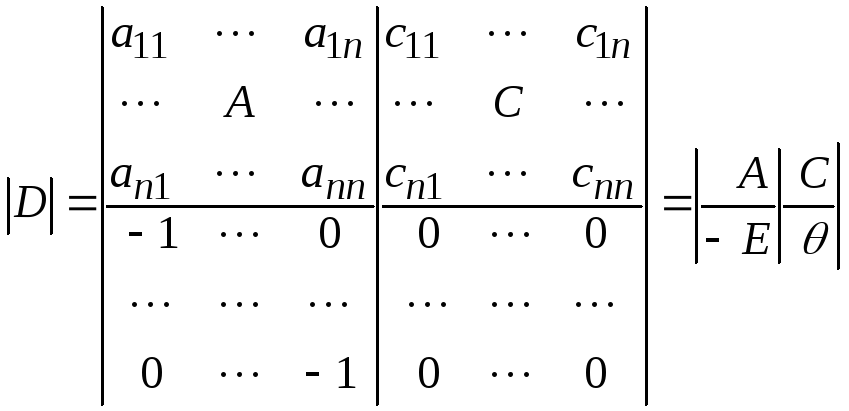
Вычислим ,разлагая его по последним столбцам. Получим , где.

Тогда и. Но нетрудно проверить, что.□

Пусть иматрицы порядка. Матрицаназываетсяобратной для матрицы , если. Матрицаназываетсяневырожденной, если .

ЛЕММА (к теореме об обратной матрице).

(а) если имеет обратную матрицу, то- невырожденная;

(б) если обратная матрица для существует, то она единственна.

ДОКАЗАТЕЛЬСТВО.

(а) Имеем . По теореме о произведении определителей получаем. Значит.

(б) Пусть также обратная матрица для. Используя ассоциативность умножения матриц, имеем.□

Оказывается утверждение (а) можно обратить.

ТЕОРЕМА (об обратной матрице). Если матрица - невырожденная матрица, то она имеет обратную матрицу, где

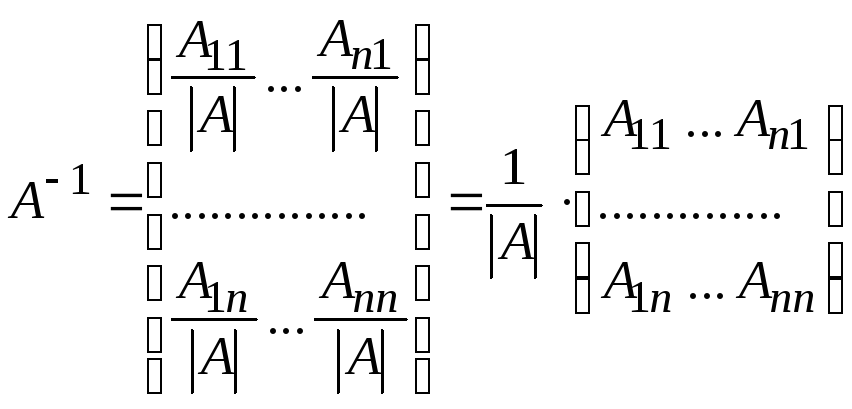(4)

Иными словами, элементравен алгебраическому дополнениюэлемента, деленному на.

ДОКАЗАТЕЛЬСТВО. Найдем элемент произведения матрицына указанную матрицу(4). Он равен

.

Но по следствиям 1 и 2 из теоремы Лапласа сумма в скобках равна , если, и равна 0, если. Следовательно. Аналогично, используя замечание после следствия 2, доказывается, что.□

Пример 7.

Дана матрица 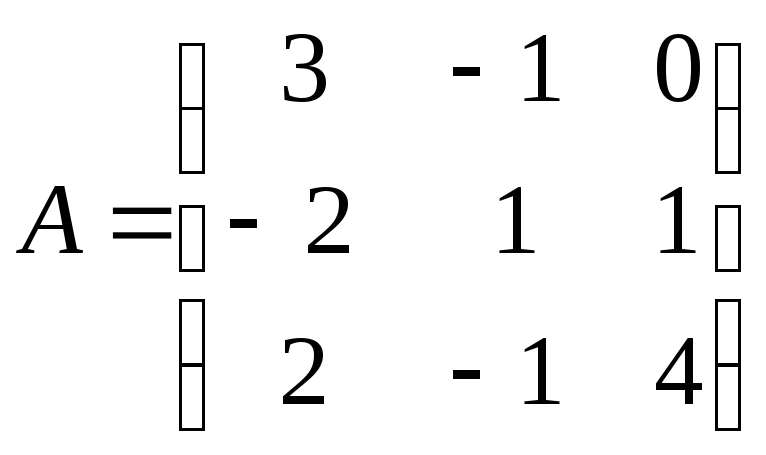. Её определитель, поэтому обратная матрицасуществует. Найдём алгебраические дополнения элементов матрицы:

;

;

;

;

.

Тогда

Линейным уравнением от неизвестныхназывается уравнением вида

.

Поэтому системой линейных уравнений (СЛУ) называется система вида

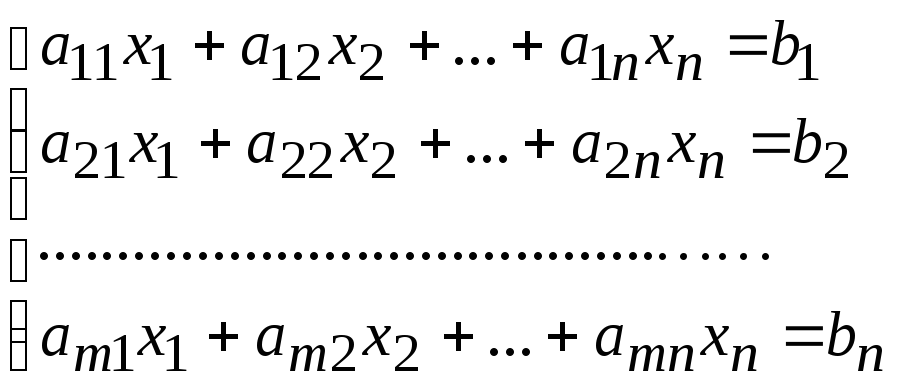(5)

Эта СЛУ состоит из уравнений отнеизвестных. Матрица, составленная из коэффициентов при неизвестных, называетсяосновной, а если к ней приписать столбец из - свободных членов СЛУ (5), то полученную матрицу называютрасширенной. СЛУ (5) можно записать и в матричном виде

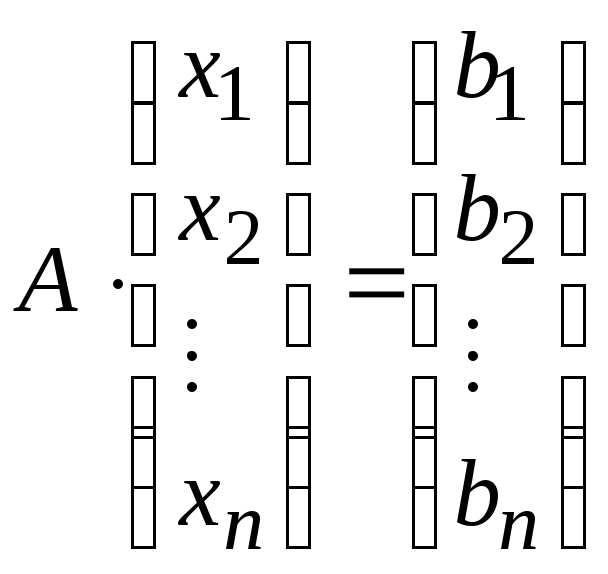(6)

СЛУ (5) называется крамеровской, если число уравнений в ней равно числу неизвестных и основная матрица ее невырожденная.

ПРАВИЛО КРАМЕРА. Крамеровская СЛУ имеет единственное решение , которое находится по формулам

,

где определитель основной матрицы СЛУ, аполучается изв результате замены встолбца на столбец из свободных членов.

ДОКАЗАТЕЛЬСТВО. Так как , то существует обратная матрица. Домножая обе части равенства (6) слева на, получим

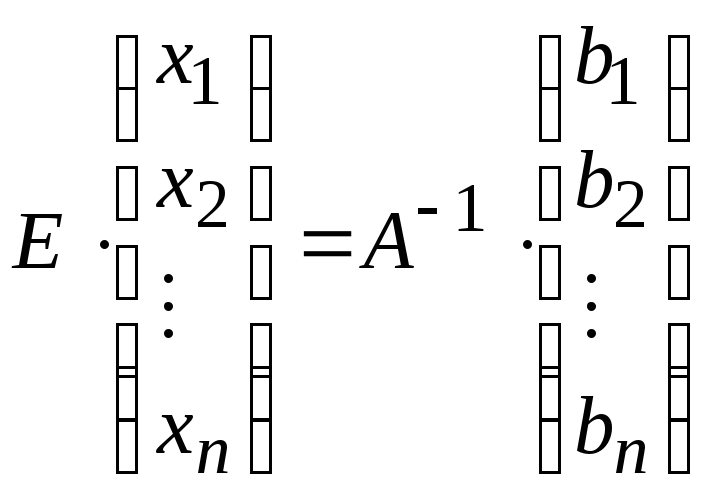(7)

Вспоминая, чему равна матрица и находя произведение в правой части (7) получаем

(8)

Но по следствию 1 из теоремы Лапласа числитель (7) есть , если вычислить, разлагаяпостолбцу.□

Пример 8. Решить систему уравнений

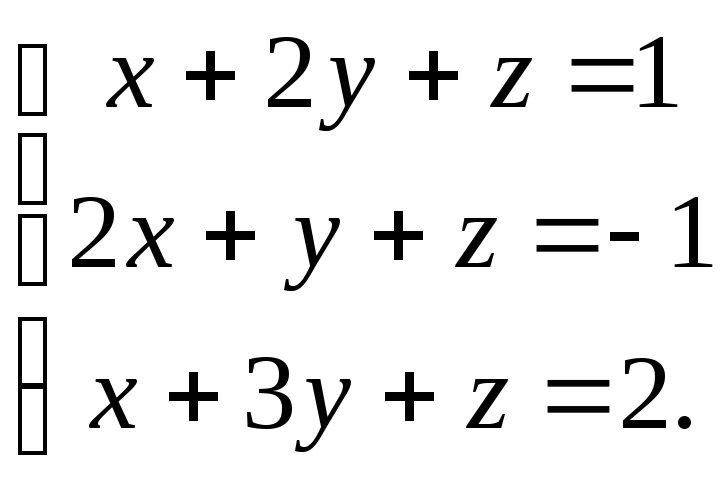
Решение.

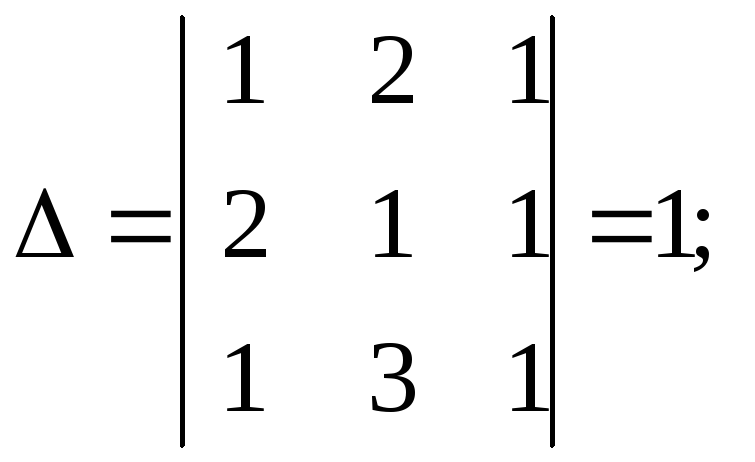
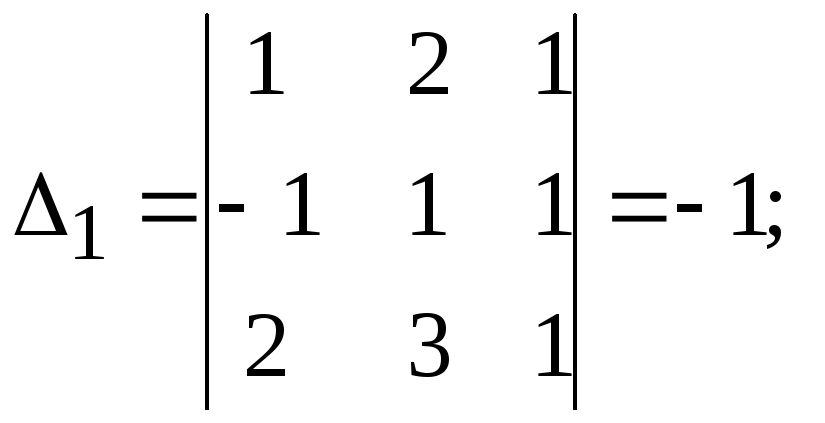
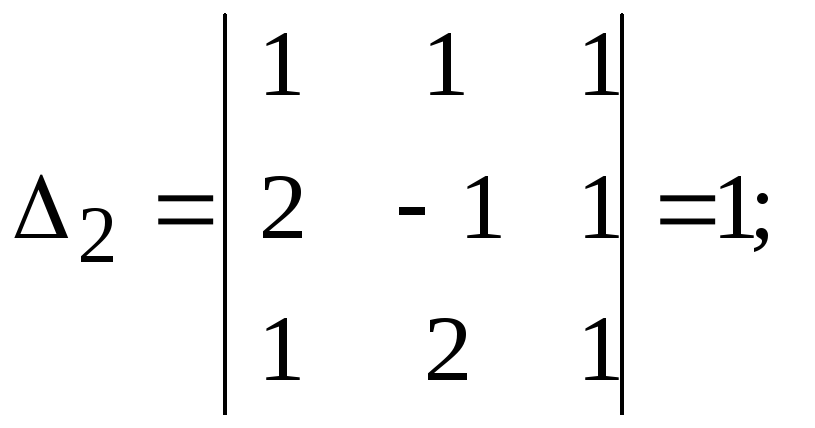
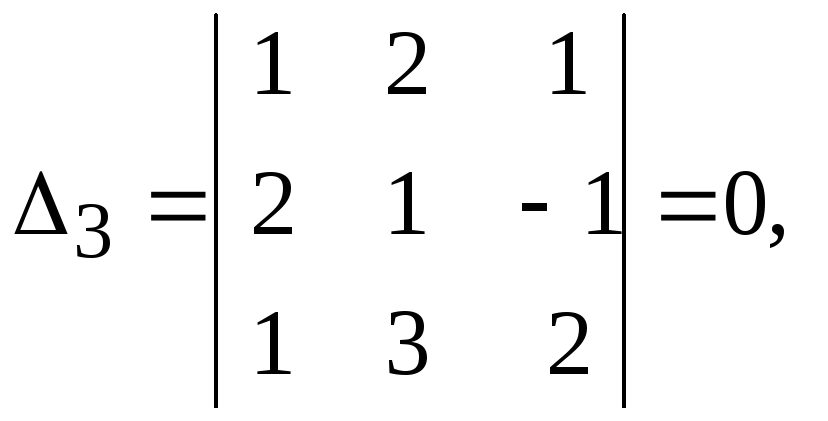
т. о.

ЗАДАЧИ К ГЛАВЕ I.

Вычислить выражения:

1.

2.

3.

4.

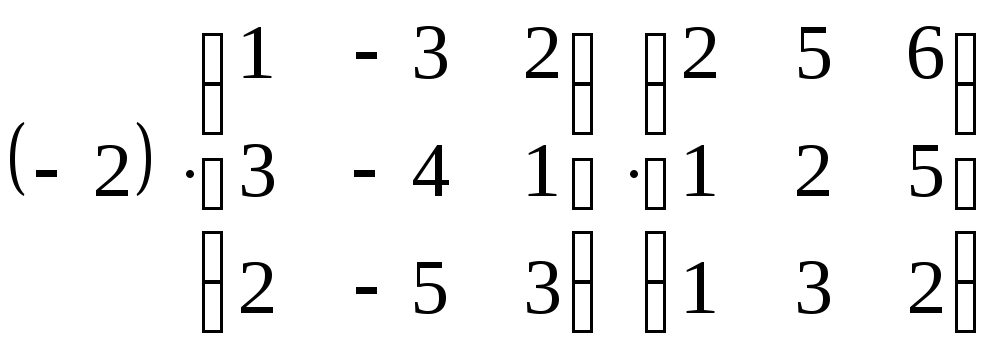
5.

6.

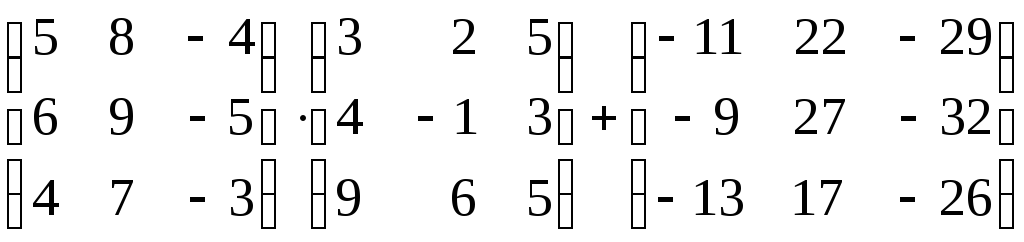
7.

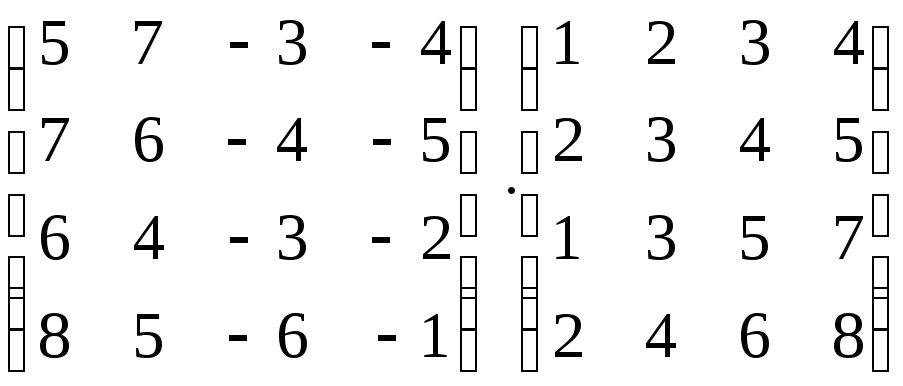
8.

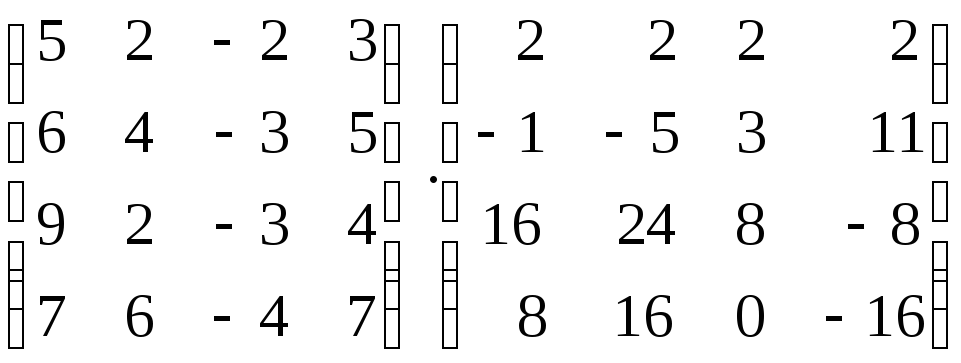
9.

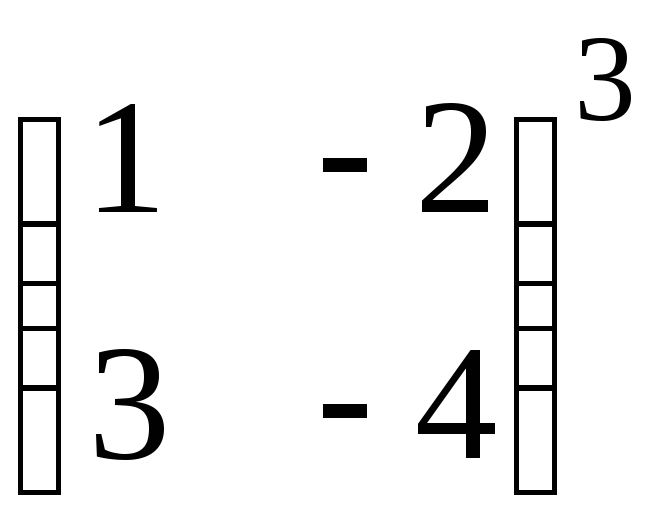
10.

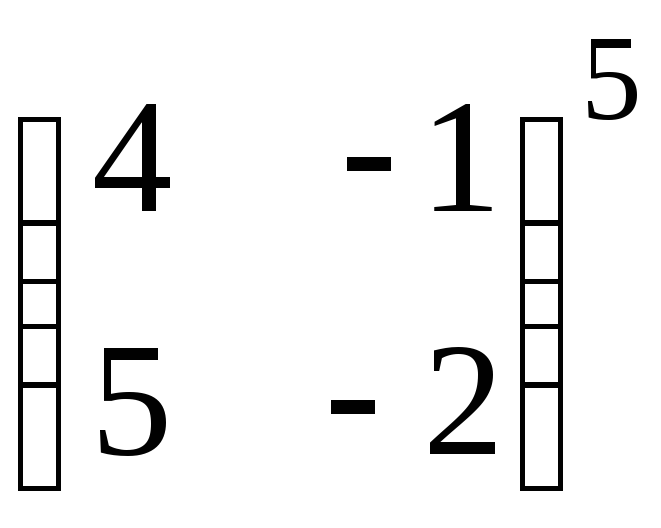
11.

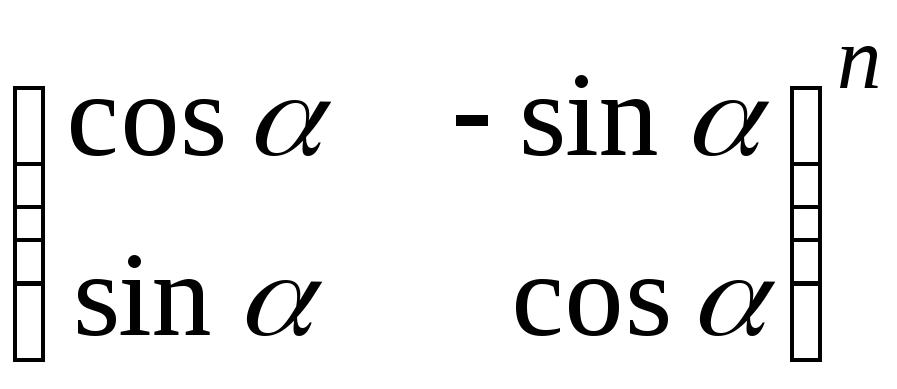
12.

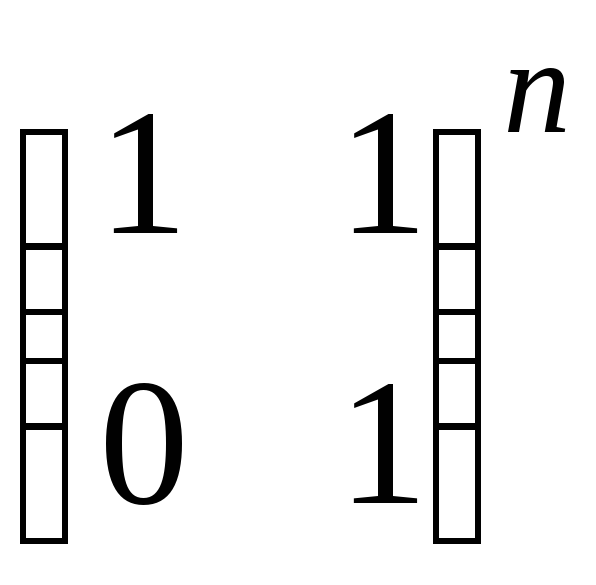
13.

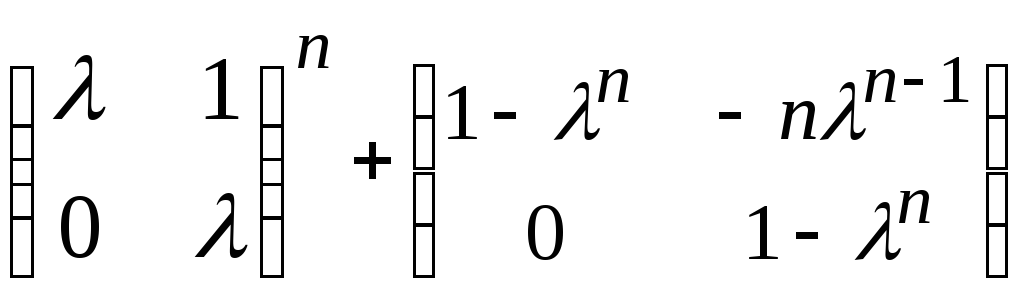
Вычислить определители:

14.

15.

16.

17.

18.

19.

20.

21.

22.

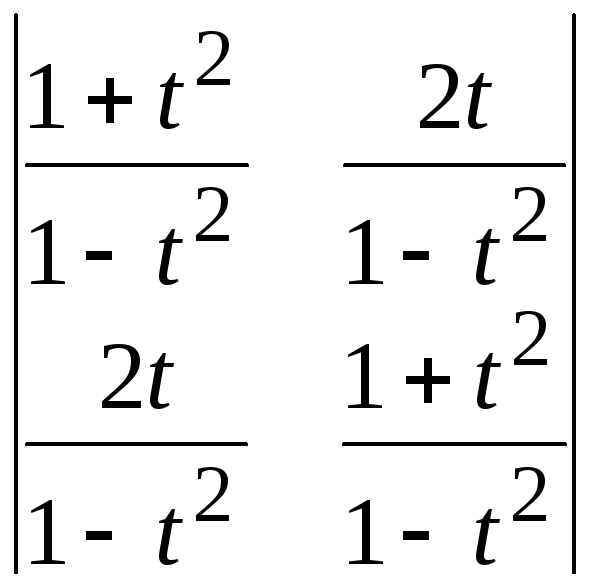
23.

24.

25.

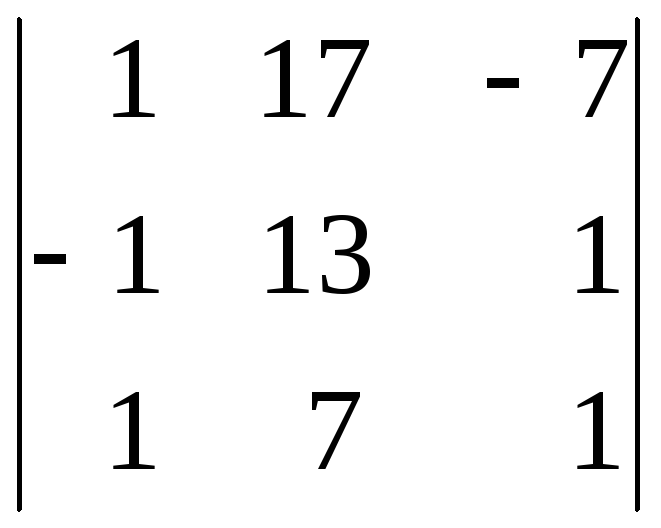
26.

27.

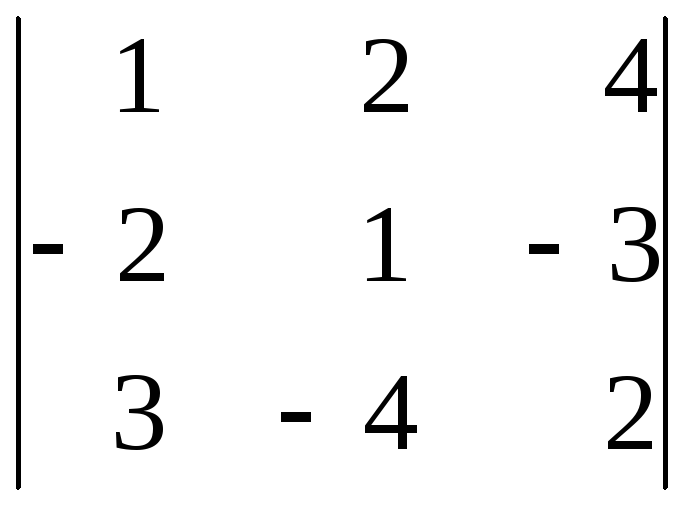
28.

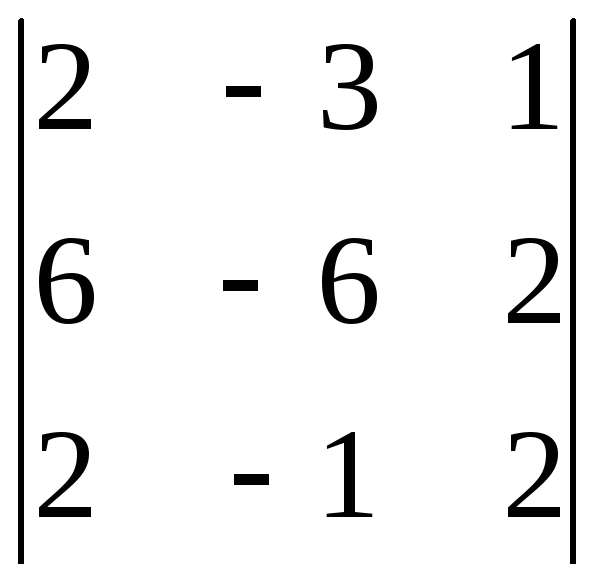
29.

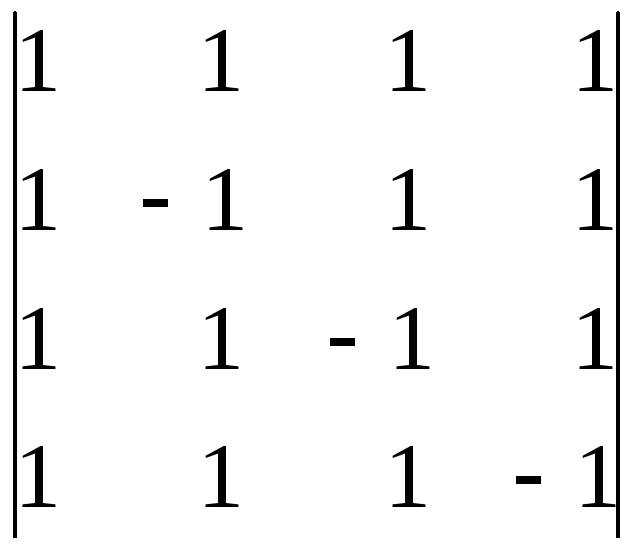
30.

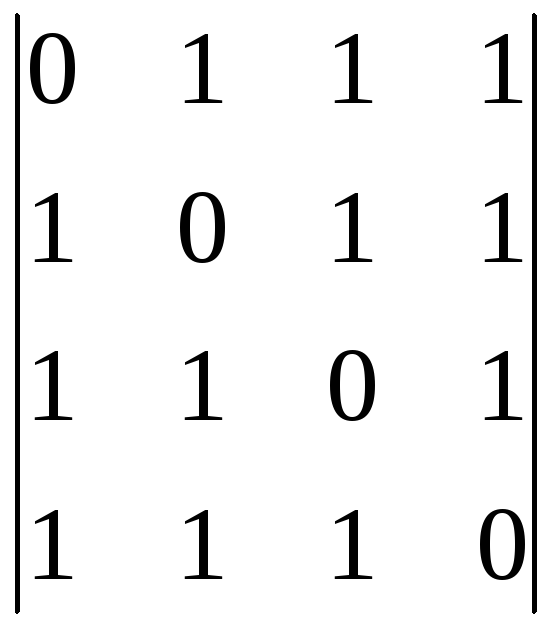
31.

32.

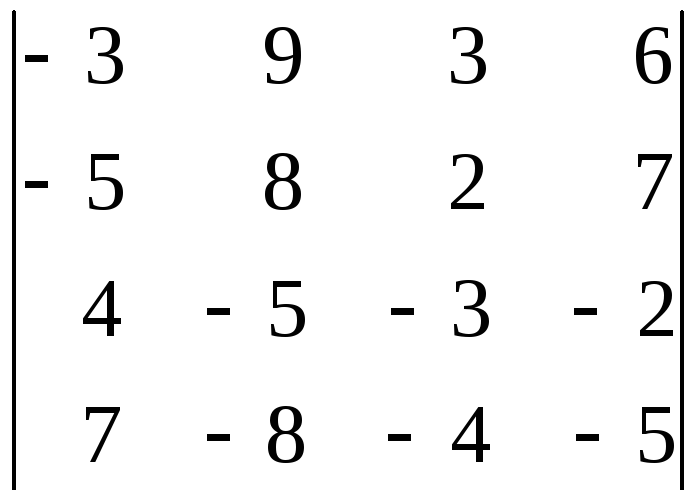
33.

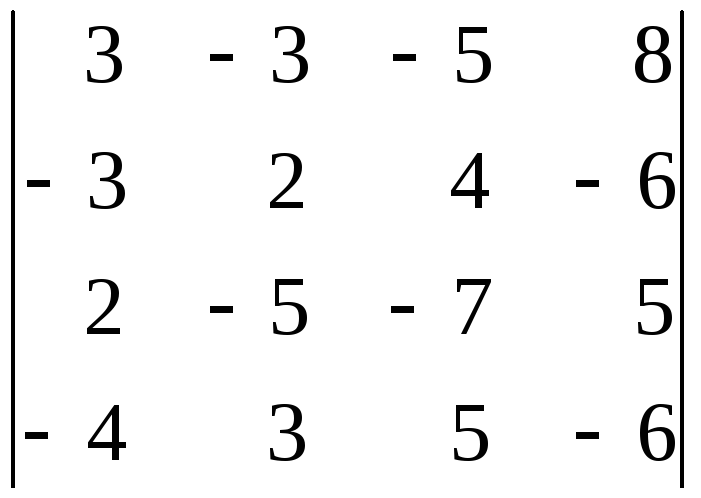
34.

35.

36.

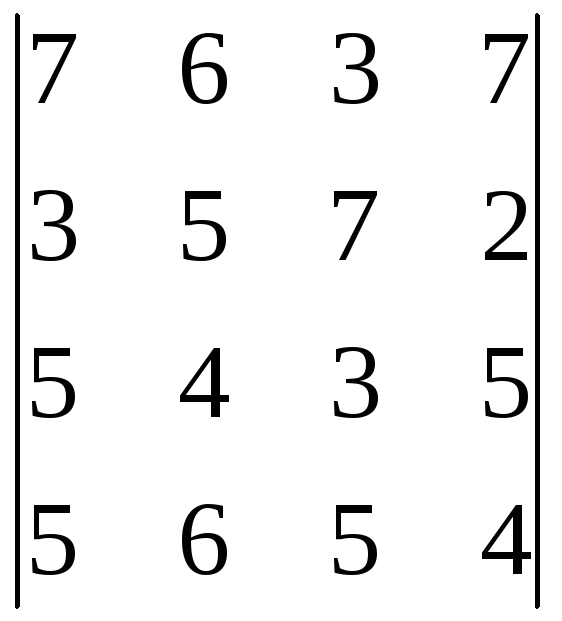
37.

38.

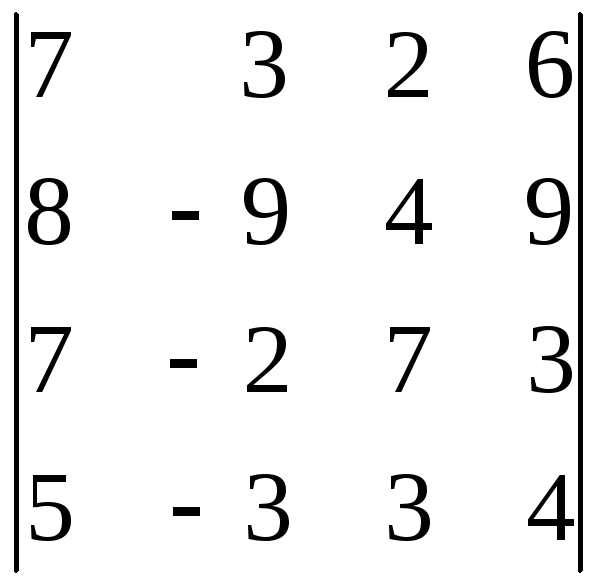
39.

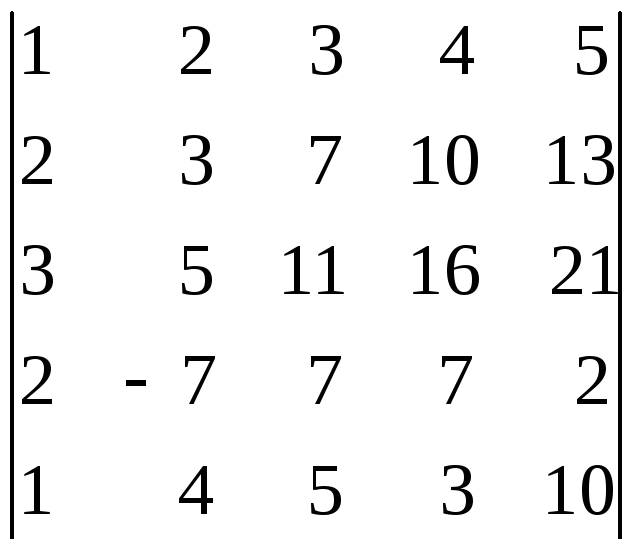
40.

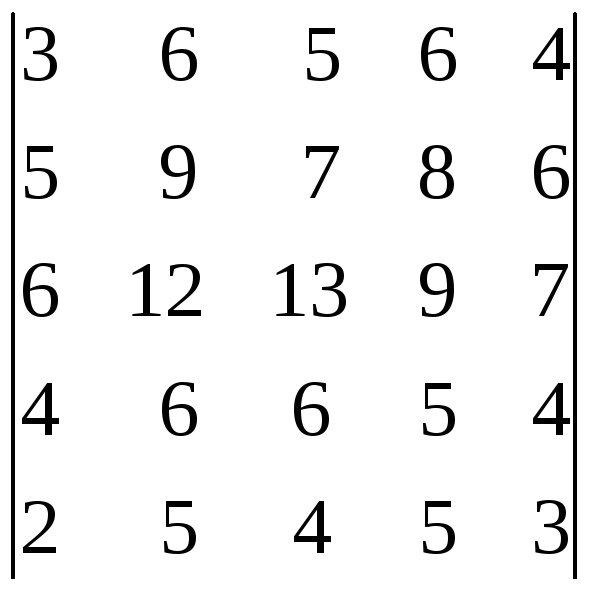
41.

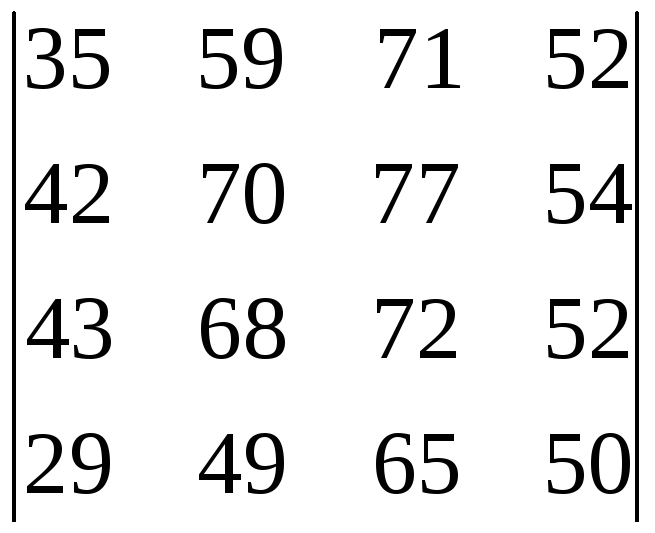
42.

43.

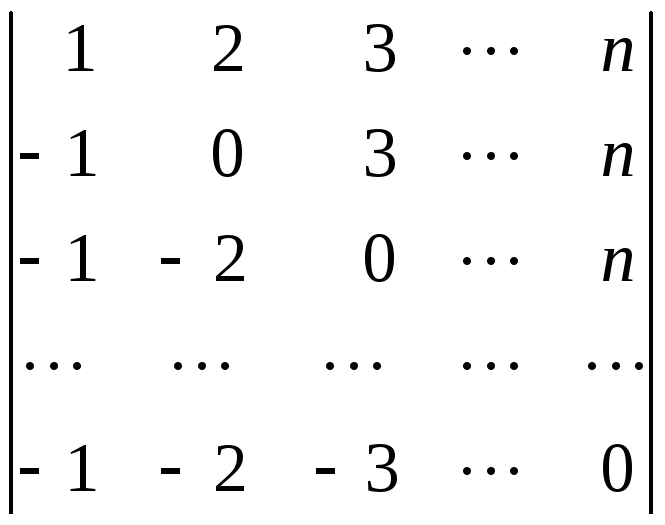
44.

45.

46.

47.

48.

49.

Доказать, что система имеет единственное решение, и найти его методом Крамера:

50.

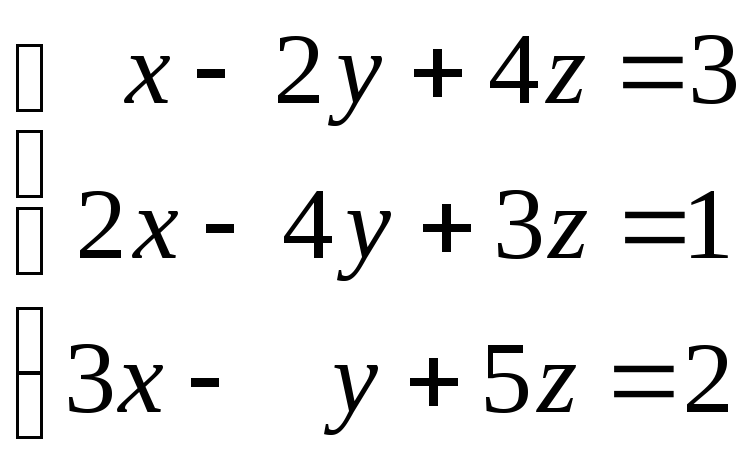
51.

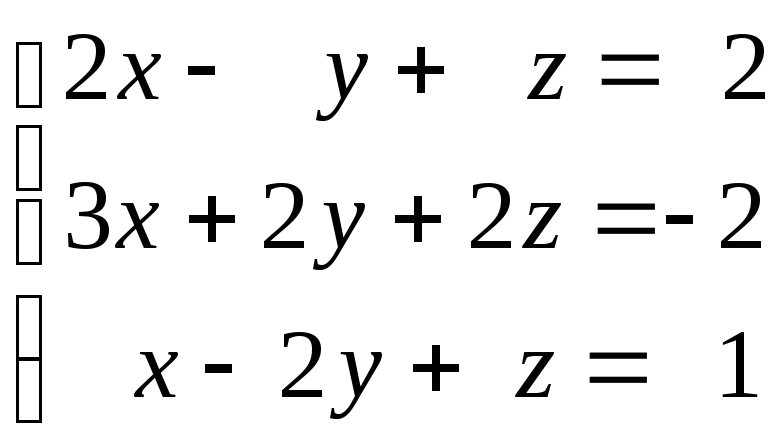
52.

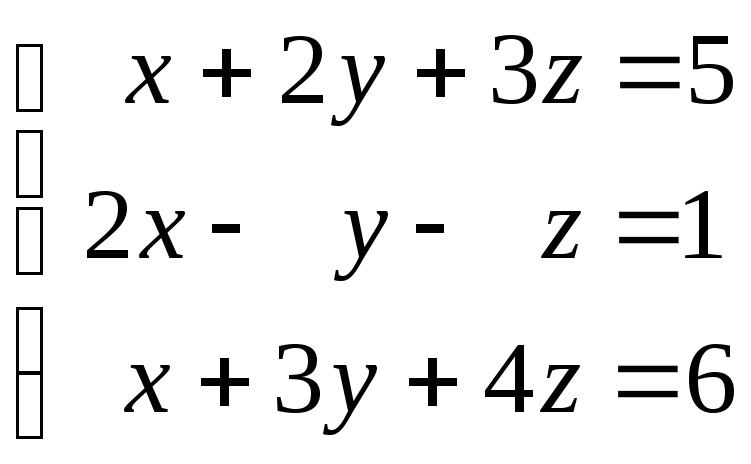
53.

54.

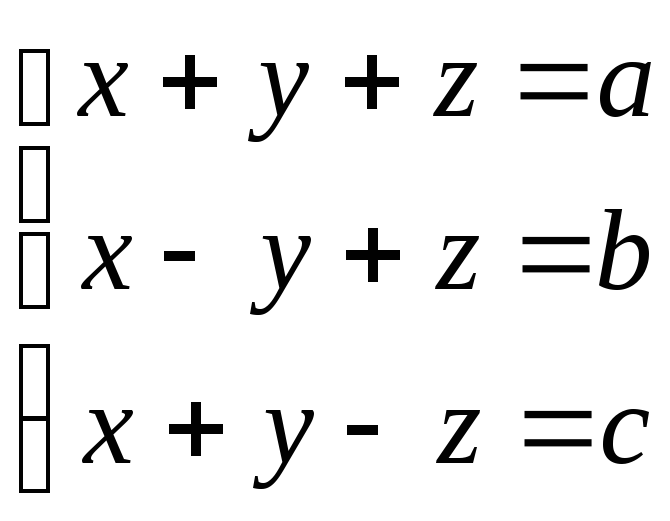
55.

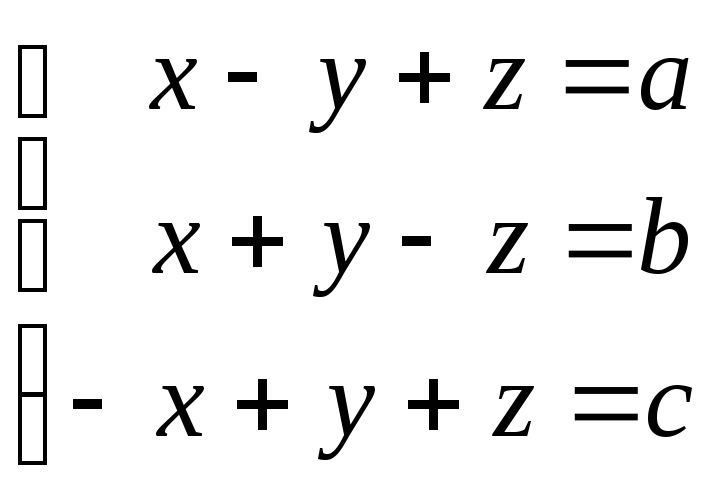
56.

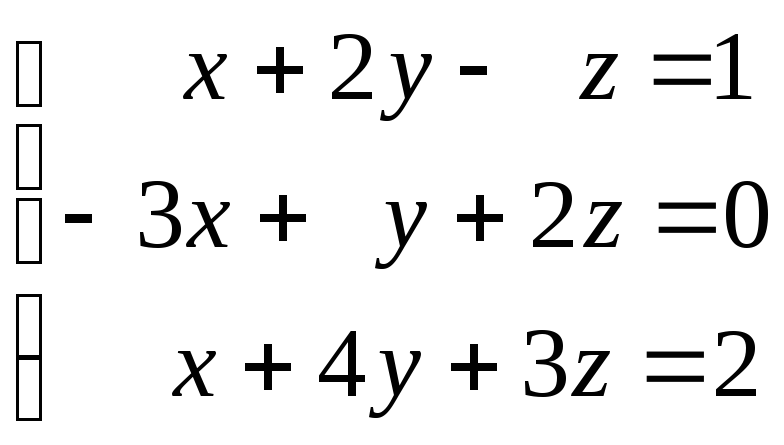
57.

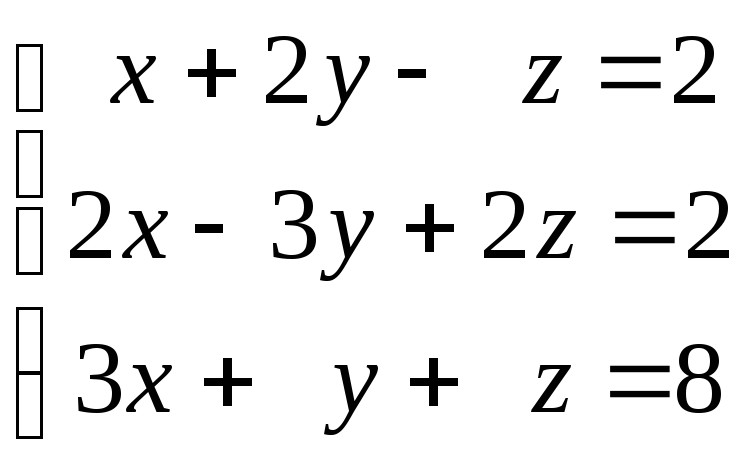
58. Определить, при каких значениях a и b система

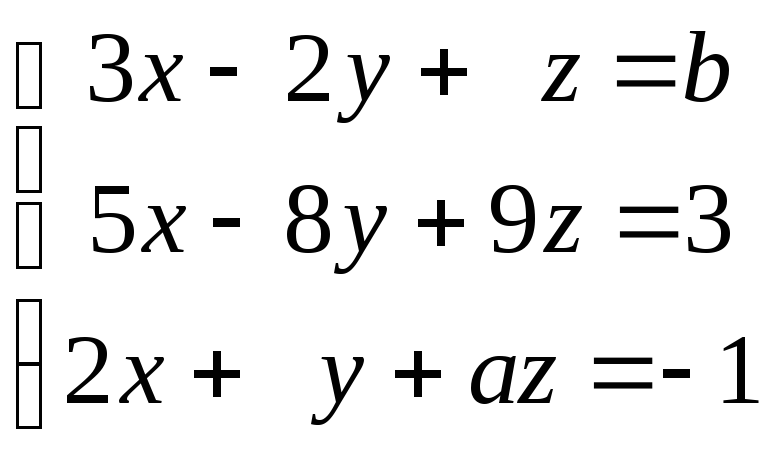
1) имеет единственное решение;

2) не имеет решений;

3) имеет бесконечно много решений.

Найти обратные матрицы для следующих матриц:

59.

60.

61.

62.

63.

64.

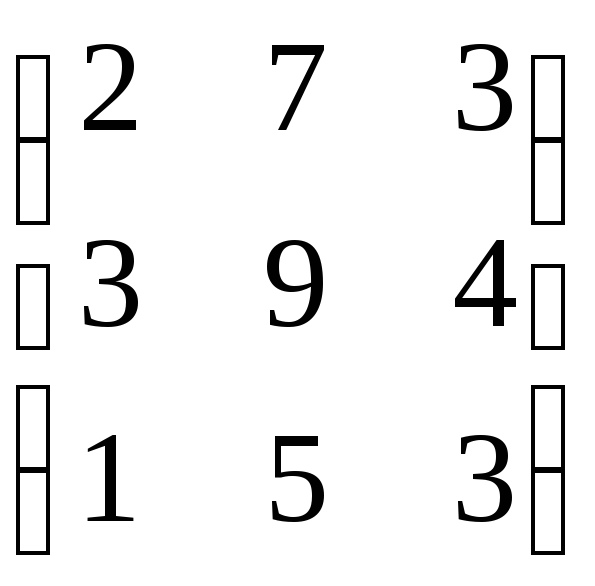
65.

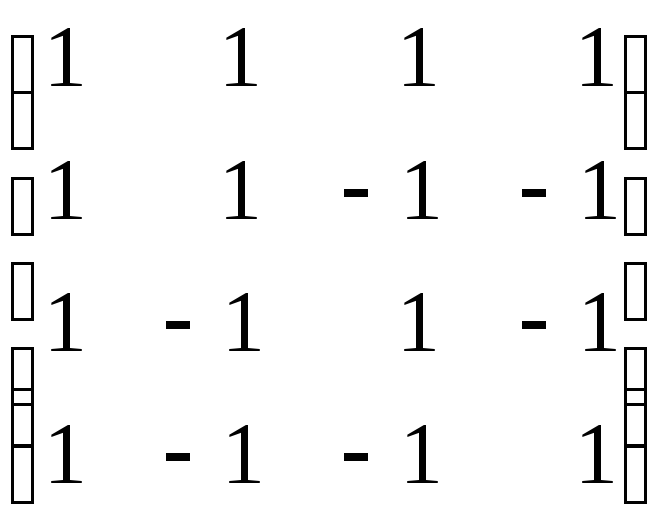
66.

67.

68.

69.

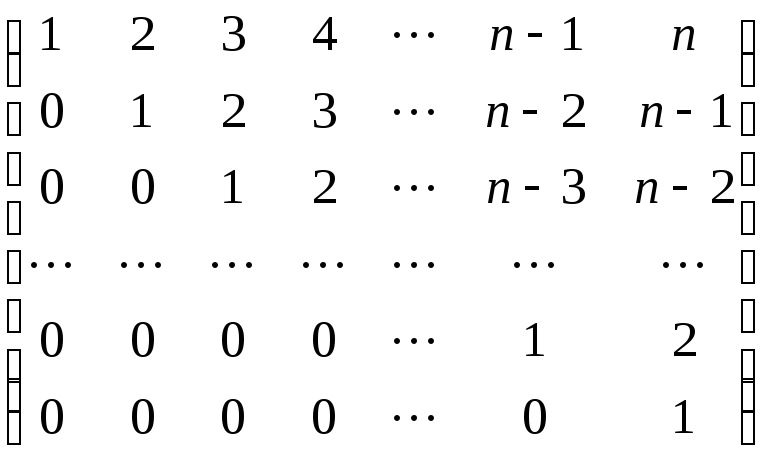
70.

Решить матричные уравнения:

71.

72.

73.

74.

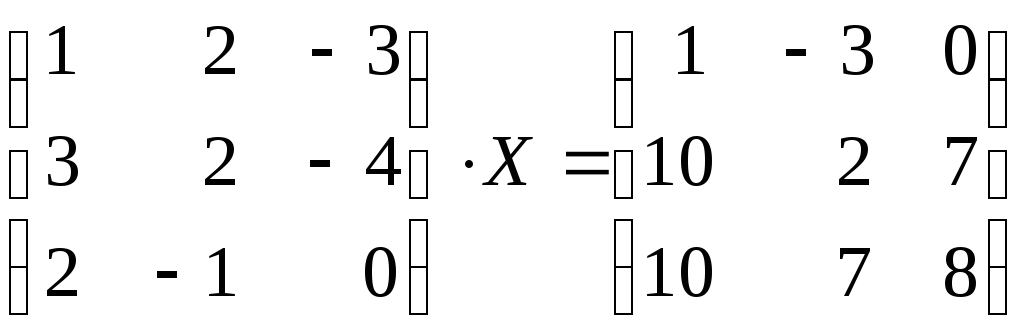
75.

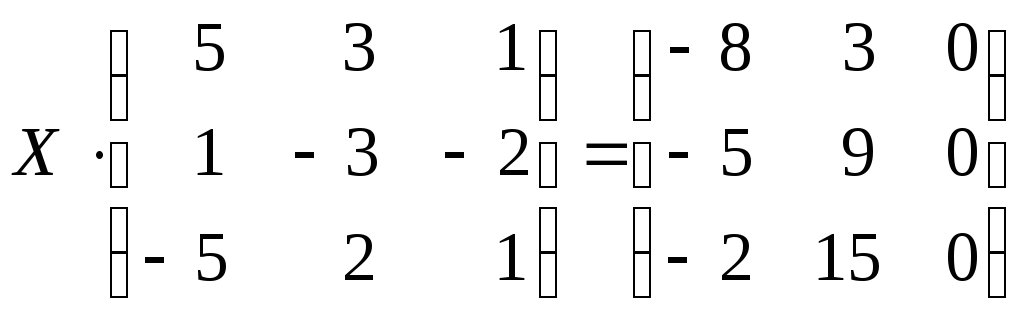
76.

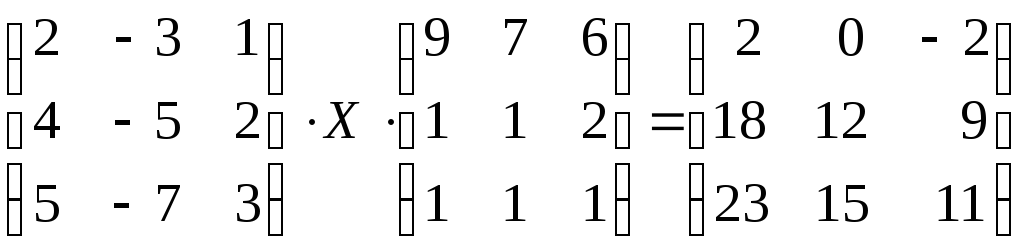
77.