
- •Глава I.
- •§1.1. Матрицы и операции над ними.
- •§1.2. Определители. Теорема Лапласа.
- •§1.3. Теоремы о произведении определителей и обратной матрице. Правило Крамера.
- •Глава II. Линейные пространства и
- •§2.1. Арифметическое линейное пространство .
- •§2.2. Ранг матриц.
- •§2.3. Системы линейных уравнений.
- •Глава 3.
- •§3.1. Матрицы линейных операторов.
- •§3.2. Ранг и дефект линейного оператора.
- •§3.3. Характеристические корни и собственные значения.
- •Глава 4.
- •§4.1. Группы, кольца, поля.
- •§4.2. Поле комплексных чисел.
- •§4.3. Поля вычетов.
- •§4.4. Кольца многочленов.
- •Глава I. Матрицы и определители. 5
§4.3. Поля вычетов.
Пусть
![]() множество всех остатков от деления
целых чисел на натуральное число
множество всех остатков от деления
целых чисел на натуральное число![]() ,
т. е.
,
т. е.![]() .Суммой
(произведением)
двух элементов будем считать остаток
от деления этой суммы (произведения)
на число
.Суммой
(произведением)
двух элементов будем считать остаток
от деления этой суммы (произведения)
на число
![]() .
Рассмотрим полученную структуру
.
Рассмотрим полученную структуру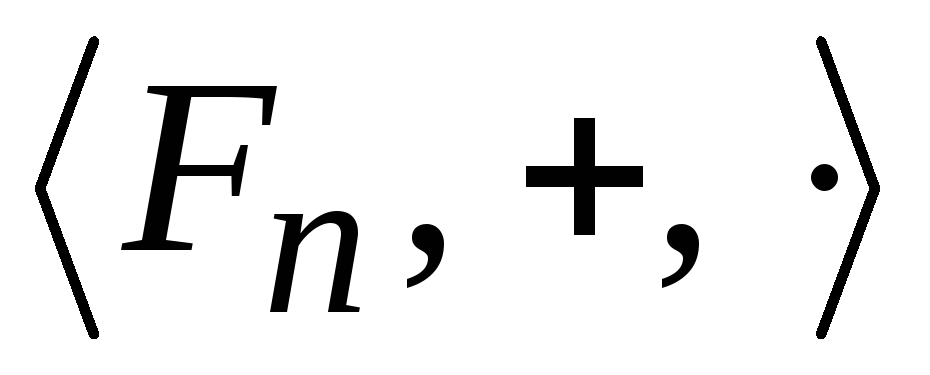 .
.
ТЕОРЕМА 6. Если
![]() составное, то
составное, то![]() не является полем.
не является полем.
ДОКАЗАТЕЛЬСТВО.
Пусть
![]() составное, т. е.
составное, т. е.
![]() ,
где
,
где![]() и
и![]() .
Тогда по модулю
.
Тогда по модулю
![]() получаем
получаем
![]() ,
но
,
но![]() и
и![]() .
Так как в поле такого быть не может
(теорема 5), то при составном
.
Так как в поле такого быть не может
(теорема 5), то при составном
![]() остатки
с операциями по модулю
остатки
с операциями по модулю
![]() не образуют поля. □
не образуют поля. □
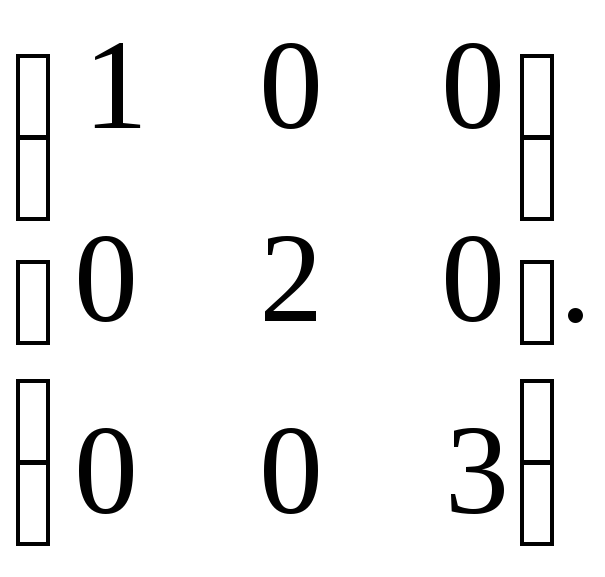
Покажем
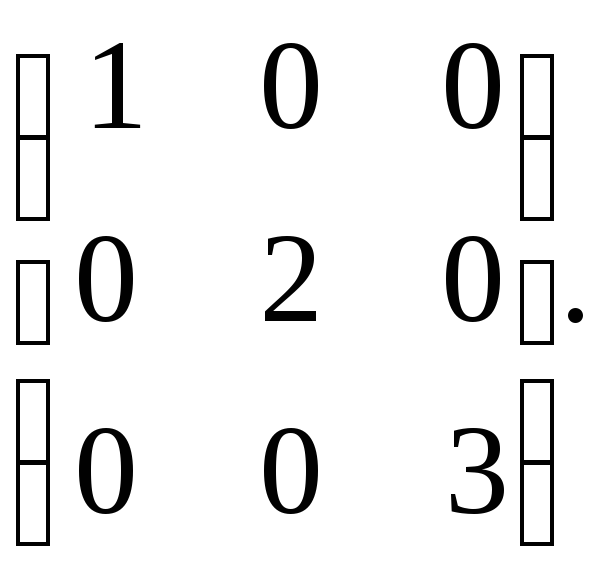
теперь, что в случае простого
![]() ,
,
![]() является полем. Вначале заметим
следующее. Пусть
является полем. Вначале заметим
следующее. Пусть
![]() и
и![]() — два целых числа,
— два целых числа,![]()
остатки от деления их на
остатки от деления их на
![]() ,
т. е.
,
т. е.
![]() и
и![]() .
Тогда
.
Тогда![]() и
и![]() ,
откуда получаем, что числа
,
откуда получаем, что числа![]() и
и![]() ,
а также числа
,
а также числа![]() и
и![]() дают при делении на
дают при делении на
![]() одинаковые остатки. Другими словами,
мы получим одинаковый результат, если
сначала возьмем остатки от деления
одинаковые остатки. Другими словами,
мы получим одинаковый результат, если
сначала возьмем остатки от деления
![]() и
и![]() на
на![]() и потом сложим (или умножим) их по модулю
и потом сложим (или умножим) их по модулю![]() ,
или, если мы сначала сложим (или умножим)
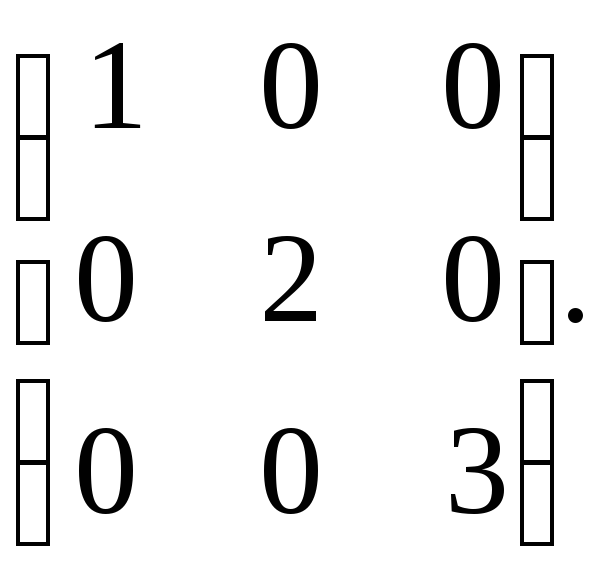
,
или, если мы сначала сложим (или умножим)![]() и
и![]() ,
как обычные натуральные числа, а затем
возьмем остаток от деления полученного
числа на
,
как обычные натуральные числа, а затем
возьмем остаток от деления полученного
числа на![]() .
Таким образом, при вычислении некоторого
выражения с операциями по модулю
.
Таким образом, при вычислении некоторого
выражения с операциями по модулю![]() можно не брать остаток от деления на
можно не брать остаток от деления на![]() после каждой операции, а произвести
вычисления сначала как с обычными
натуральными числами и обычными
операциями и только в конце взять
остаток от деления полученного числа
на
после каждой операции, а произвести
вычисления сначала как с обычными
натуральными числами и обычными
операциями и только в конце взять
остаток от деления полученного числа
на![]() .
Это позволяет утверждать, что операции
сложения и умножения ассоциативны и
коммутативны, а также справедлива
дистрибутивность умножения относительно
сложения.
.
Это позволяет утверждать, что операции
сложения и умножения ассоциативны и
коммутативны, а также справедлива
дистрибутивность умножения относительно
сложения.
Нейтральным
элементом по сложению является
![]() ,
а единичным элементом по умножению
,
а единичным элементом по умножению
![]() .
Остается показать, что при
.
Остается показать, что при![]() простом у каждого остатка
простом у каждого остатка![]() ,
отличного от
,
отличного от![]() ,
есть обратный, т. е. что найдется остаток
,
есть обратный, т. е. что найдется остаток![]() такой, что
такой, что![]() по модулю
по модулю![]() .
Итак, пусть
.
Итак, пусть![]() .
Рассмотрим числа
.
Рассмотрим числа
![]() (умножение обычное).
(умножение обычное).
Разность
любых двух из этих чисел
![]() не делится на
не делится на![]() ,
так как
,
так как![]() простое, а
простое, а![]() и
и![]() .
Таким образом, все эти
.
Таким образом, все эти![]() чисел дают разные и, следовательно,
всевозможные остатки при делении на
чисел дают разные и, следовательно,
всевозможные остатки при делении на![]() .
Значит, одно из этих чисел дает при
делении на
.
Значит, одно из этих чисел дает при
делении на![]() остаток
остаток![]() ,
т. е.
,
т. е.![]() по модулю
по модулю![]() для некоторого остатка
для некоторого остатка![]() .
.
Таким
образом, при
![]() простом все свойства поля выполняются.
простом все свойства поля выполняются.
В качестве примера приведём таблицы сложения и умножения элементов поля вычетов по модулю 5.
|
|
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
0 |
|
2 |
2 |
3 |
4 |
0 |
1 |
|
3 |
3 |
4 |
0 |
1 |
2 |
|
4 |
4 |
0 |
1 |
2 |
3 |
|
|
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 |
|
2 |
0 |
2 |
4 |
1 |
3 |
|
3 |
0 |
3 |
1 |
4 |
2 |
|
4 |
0 |
4 |
3 |
2 |
1 |
По этим таблицам также можно получить разность и частное любых двух элементов.
§4.4. Кольца многочленов.
Пусть
![]() произвольное поле. Через
произвольное поле. Через![]() обозначим множество многочленов от
обозначим множество многочленов от![]() с коэффициентами из
с коэффициентами из![]() .
Многочлен имеет вид:
.
Многочлен имеет вид:
![]() .
.
Если коэффициент
![]() отличен от нулевого элемента поля
отличен от нулевого элемента поля![]() ,
то его называютстаршим
коэффициентом
,
то его называютстаршим
коэффициентом
![]() ,
а число
,
а число![]() степенью
многочлена.
Сами ненулевые элементы поля
степенью
многочлена.
Сами ненулевые элементы поля
![]() будут являться многочленами нулевой
степени, а нулевой элемент
многочленом неопределённой степени.
будут являться многочленами нулевой
степени, а нулевой элемент
многочленом неопределённой степени.
Если все коэффициенты
многочлена
комплексные числа, то
![]() называют множеством многочленов над
полем комплексных чисел. Определим во
множестве
называют множеством многочленов над
полем комплексных чисел. Определим во
множестве![]() операции сложения и умножения следующим
образом. Для произвольных многочленов
операции сложения и умножения следующим
образом. Для произвольных многочленов![]() и
и![]() ,
таких что:
,
таких что:
![]()
![]()
и
![]() ,
ихсуммой
назовём многочлен
,
ихсуммой
назовём многочлен
![]() ,
,
коэффициенты
которого получаются сложением
коэффициентов многочленов
![]() и
и![]() ,
стоящих при одинаковых степенях
неизвестного,
т. е.
,
стоящих при одинаковых степенях
неизвестного,
т. е.![]() причём при
причём при![]() коэффициенты
коэффициенты![]() следует считать равными нулю.Степень
суммы будет равна
следует считать равными нулю.Степень
суммы будет равна
![]() ,
если
,
если
![]() больше
больше![]() ,
но
при
,
но
при
![]() она может случайно оказаться меньше
она может случайно оказаться меньше![]() ,
а
именно в случае
,
а
именно в случае
![]() .
.
Произведением
многочленов
![]() и
и![]() называется
многочлен
называется
многочлен
![]() ,
,
коэффициенты которого определяются следующим образом:
![]() ,
,
т. е.
коэффициент
![]() есть
результат перемножения таких коэффициентов
многочленов
есть
результат перемножения таких коэффициентов
многочленов
![]() и
и![]() ,
сумма
индексов которых равна
,
сумма
индексов которых равна
![]() ,
и
сложения всех таких произведений; в
частности,
,
и
сложения всех таких произведений; в
частности,
![]() .
Из последнего равенства вытекает
неравенство
.
Из последнего равенства вытекает
неравенство![]() и поэтомустепень
произведения, двух многочленов равна
сумме степеней этих многочленов. Отсюда
следует, что произведение
многочленов, отличных от нуля, никогда
не будет равным нулю.
и поэтомустепень
произведения, двух многочленов равна
сумме степеней этих многочленов. Отсюда
следует, что произведение
многочленов, отличных от нуля, никогда
не будет равным нулю.
Какими
свойствами обладают введенные нами
операции для многочленов? Коммутативность
и ассоциативность сложения немедленно
вытекают из справедливости этих свойств
для сложения чисел, так как складываются
коэффициенты при каждой степени
неизвестного отдельно. Вычитание
оказывается выполнимым: роль нуля
играет число нуль, включенное нами в
число многочленов, а противоположным
для записанного выше многочлена
![]() будет
многочлен
будет
многочлен
![]()
Коммутативность
умножения
вытекает из коммутативности умножения
чисел и того факта, что в определении
произведения многочленов коэффициенты
обоих множителей
![]() и
и![]() используются
совершенно равноправным образом.
Ассоциативность умножения доказывается
следующим образом: если, помимо
многочленов
используются
совершенно равноправным образом.
Ассоциативность умножения доказывается
следующим образом: если, помимо
многочленов
![]() и
и![]() ,
дан
еще многочлен
,
дан
еще многочлен
![]() ,
,
то
коэффициентом при
![]() в произведении
в произведении![]() будет
служить число
будет
служить число
![]() ,
,
а в
произведении
![]()
равное ему число
равное ему число
![]() .
.
Наконец, справедливость закона дистрибутивности вытекает из равенства
![]() ,
,
так
как левая часть этого равенства является
коэффициентом при
![]() в многочлене
в многочлене![]() ,
а
правая часть
коэффициентом при той же степени
неизвестного в многочлене
,
а
правая часть
коэффициентом при той же степени
неизвестного в многочлене
![]() .
.
Заметим,
что роль единицы при умножении многочленов
играет
число 1, рассматриваемое как
многочлен нулевой степени. С другой
стороны, многочлен
![]() тогда и только тогда обладает обратным
многочленом
тогда и только тогда обладает обратным
многочленом
![]() ,
,
![]() (1),
(1),
если
![]() является многочленом нулевой степени.
Действительно,
если
является многочленом нулевой степени.
Действительно,
если
![]() является
отличным от нуля числом
является
отличным от нуля числом
![]() ,
то обратным многочленом служит для
него число
,
то обратным многочленом служит для
него число![]() .
Если же
.
Если же
![]() имеет
степень
имеет
степень
![]() ,
то степень левой части равенства (1),
если бы многочлен
,
то степень левой части равенства (1),
если бы многочлен
![]() существовал,
была бы не меньше
существовал,
была бы не меньше
![]() ,
в
то время как справа стоит многочлен
нулевой степени.
Отсюда
вытекает, что для
умножения многочленов обратная операция
деление
не
существует.
,
в
то время как справа стоит многочлен
нулевой степени.
Отсюда
вытекает, что для
умножения многочленов обратная операция
деление
не
существует.
Следовательно,
множество
![]() с введёнными таким образом операциями
сложения и умножения образует
коммутативное кольцо с единицей, но не
поле. Это же утверждение будет справедливо
для многочленов над произвольным полем.
с введёнными таким образом операциями
сложения и умножения образует
коммутативное кольцо с единицей, но не
поле. Это же утверждение будет справедливо
для многочленов над произвольным полем.
ТЕОРЕМА 7. Для
любых двух многочленов
![]() и
и![]() можно найти такие многочлены
можно найти такие многочлены![]() и
и![]() ,
что
,
что
![]() ,
(2)
,
(2)
причем
степень
![]() меньше степени
меньше степени![]() или же
или же![]() .
Многочлены
.
Многочлены
![]() и
и![]() ,
удовлетворяющие этому условию,
определяются однозначно.
,
удовлетворяющие этому условию,
определяются однозначно.
ДОКАЗАТЕЛЬСТВО.
Докажем сперва вторую половину теоремы.
Пусть существуют еще многочлены
![]() и
и![]() ,
также удовлетворяющие равенству
,
также удовлетворяющие равенству
![]() ,
(3)
,
(3)
причем
степень
![]() снова
меньше степени
снова
меньше степени
![]() (или же
(или же
![]() ).
Приравнивая друг другу правые части
равенств (2) и (3), получим:
).
Приравнивая друг другу правые части
равенств (2) и (3), получим:
![]() .
.
Степень
правой части этого равенства меньше
степени
![]() ,
степень же левой части была бы при
,
степень же левой части была бы при
![]() больше или равна степени
больше или равна степени
![]() .
Поэтому
должно быть
.
Поэтому
должно быть
![]() ,
т.
е.
,
т.
е.
![]() ,
а
тогда и
,
а
тогда и
![]() .
.
Переходим
к доказательству первой половины
теоремы. Пусть многочлены
![]() и
и
![]() имеют
соответственно степени
имеют
соответственно степени
![]() и
и![]() .
.
![]()
![]()
Если
![]() ,
то можно положить
,
то можно положить![]() ,
,![]() .
Если
же
.
Если
же
![]() ,
то
воспользуемся индукцией по степени
,
то
воспользуемся индукцией по степени
![]() .
Пусть утверждение справедливо для
степеней, меньших
.
Пусть утверждение справедливо для
степеней, меньших![]() .
Положив
.
Положив
![]() ,
,
получим
многочлен, степень которого меньше
![]() .
По предположению индукции, существуют
многочлены
.
По предположению индукции, существуют
многочлены
![]() и
и
![]() такие, что
такие, что
![]() ,
где степень
,
где степень
![]() строго меньше степени
строго меньше степени
![]() .
Тогда
.
Тогда
![]() .
□
.
□
Как и в случае
чисел,
![]() и
и
![]() называют соответственно частным
и остатком
от деления
называют соответственно частным
и остатком
от деления
![]() на
на
![]() .
Если
.
Если
![]() ,
то говорят, что
,
то говорят, что
![]() делит
делит
![]() или
или
![]() делится на
делится на
![]() (без остатка). В этом случае многочлен
(без остатка). В этом случае многочлен
![]() называется делителем
многочлена
называется делителем
многочлена
![]() .
.
Очевидно,
что многочлен
![]() тогда и только тогда будет делителем
многочлена
тогда и только тогда будет делителем
многочлена
![]() ,
если существует многочлен
,
если существует многочлен
![]() ,
удовлетворяющих равенству
,
удовлетворяющих равенству
![]() .
.
Действительно,
если
![]() является делителем для
является делителем для
![]() ,
то в качестве
,
то в качестве
![]() следует взять частное от деления
следует взять частное от деления
![]() на
на
![]() .
Обратно, пусть такой многочлен
.
Обратно, пусть такой многочлен
![]() существует. Из
единственности многочленов
существует. Из
единственности многочленов
![]() и
и
![]() ,
удовлетворяющих
равенству
,
удовлетворяющих
равенству
![]()
и
условию, что степень
![]() меньше
степени
меньше
степени
![]() ,
в нашем случае следует,
что частное от деления
,
в нашем случае следует,
что частное от деления
![]() на
на
![]() равно
равно
![]() ,
а
остаток равен
нулю.
,
а
остаток равен
нулю.
Укажем некоторые основные свойства делимости многочленов, которые найдут в дальнейшем многочисленные применения.
Свойство 1.
Если
![]() делится на
делится на
![]() ,
a
,
a
![]() делится на
делится на
![]() ,
то
,
то
![]() будет
делиться на
будет
делиться на
![]() .
.
В
самом деле, по условию
![]() и
и
![]() ,
а
поэтому
,
а
поэтому
![]() .
.
Свойство 2. Если
![]() и
и
![]() делятся на
делятся на
![]() ,
то их сумма и разность
также делятся на
,
то их сумма и разность
также делятся на
![]() .
.
Действительно,
из равенств
![]() и
и![]() вытекает
вытекает
![]() .
.
Свойство 3. Если
![]() делится на
делится на
![]() ,
то произведение
,
то произведение
![]() на любой многочлен
на любой многочлен
![]() также будет делиться на
также будет делиться на
![]() .
.
Действительно,
если
![]() ,
то
,
то![]() .
.
Из свойств 2 и 3 вытекает:
Свойство 4. Если
каждый из многочленов
![]() делится
на
делится
на
![]() ,
то на
,
то на
![]() будет
делиться и многочлен
будет
делиться и многочлен
![]() ,
,
где
![]() произвольные
многочлены.
произвольные
многочлены.
Свойство 5. Всякий
многочлен
![]() делится на любой многочлен нулевой
степени.
делится на любой многочлен нулевой
степени.
Действительно,
если
![]() ,
а
,
а
![]() произвольное
число, не равное нулю, т. е. произвольный
многочлен нулевой
степени, то
произвольное
число, не равное нулю, т. е. произвольный
многочлен нулевой
степени, то
![]() .
.
Свойство 6. Если
![]() делится на
делится на
![]() ,
то
,
то
![]() делится и на
делится и на
![]() ,где
,где
![]() произвольное число, отличное от нуля.
произвольное число, отличное от нуля.
В
самом деле, из равенства
![]() следует
равенство
следует
равенство
![]() .
.
Свойство 7.
Многочлены
![]() ,
,![]() ,
и
только они будут делителями многочлена
,
и
только они будут делителями многочлена
![]() ,
имеющими такую же степень, что и
,
имеющими такую же степень, что и
![]() .
.
Действительно,
![]() ,
т.
е.
,
т.
е.
![]() делится
на
делится
на
![]() .
Если,
с другой стороны,
.
Если,
с другой стороны,
![]() делится
на
делится
на
![]() ,
причем степени
,
причем степени
![]() и
и
![]() совпадают,
то степень частного от деления
совпадают,
то степень частного от деления
![]() на
на
![]() должна
быть равной нулю, т. е.
должна
быть равной нулю, т. е.
![]() ,
,
![]() ,откуда
,откуда
![]() .
.
Отсюда вытекает следующее свойство:
Свойство 8. Тогда
и только тогда многочлены
![]() ,
,
![]() одновременно делятся
друг на друга, когда
одновременно делятся
друг на друга, когда
![]() .
.
Наконец, из свойств 8 и 1 вытекает:
Свойство 9. Всякий
делитель одного из двух многочленов
![]() ,
,
![]() ,где
,где
![]() ,
будет
делителем и для другого многочлена.
,
будет
делителем и для другого многочлена.
Пусть
даны произвольные многочлены
![]() и
и
![]() .
Многочлен
.
Многочлен
![]() будет называться общим
делителем
для
будет называться общим
делителем
для
![]() и
и
![]() ,
если
он служит делителем для каждого из этих
многочленов. Свойство 5 показывает, что
к числу общих
делителей многочленов
,
если
он служит делителем для каждого из этих
многочленов. Свойство 5 показывает, что
к числу общих
делителей многочленов
![]() и
и
![]() принадлежат
все многочлены
нулевой степени. Если других общих
делителей эти два многочлена
не имеют, то они называются взаимно
простыми.
принадлежат
все многочлены
нулевой степени. Если других общих
делителей эти два многочлена
не имеют, то они называются взаимно
простыми.
Наибольшим
общим делителем отличных
от нуля многочленов
![]() и
и
![]() называется
такой многочлен
называется
такой многочлен
![]() ,
который
является их
общим делителем и, вместе с тем, сам
делится на любой другой общий
делитель, этих многочленов. Обозначается
наибольший общий делитель
многочленов
,
который
является их
общим делителем и, вместе с тем, сам
делится на любой другой общий
делитель, этих многочленов. Обозначается
наибольший общий делитель
многочленов
![]() и
и
![]() символом
символом
![]() .
.
Это
определение оставляет открытым вопрос,
существует ли наибольший
общий делитель для любых многочленов
![]() и
и
![]() .
Положительный
ответ на этот вопрос, а так же метод для
практического разыскания наибольшего
общего делителя
даёт алгоритм
последовательного деления или
алгоритм
Евклида,
который состоит
в следующем. Пусть даны многочлены
.
Положительный
ответ на этот вопрос, а так же метод для
практического разыскания наибольшего
общего делителя
даёт алгоритм
последовательного деления или
алгоритм
Евклида,
который состоит
в следующем. Пусть даны многочлены
![]() и
и![]() .
Делим
.
Делим![]() на
на![]() и получаем некоторый остаток
и получаем некоторый остаток![]() .
Делим затем
.
Делим затем![]() на
на![]() и получаем остаток
и получаем остаток![]() ,
делим
,
делим![]() на
на![]() и т. д. Так как степени остатков все
время понижаются, то в этой цепочке
последовательных делений мы должны
дойти до такого места, на котором деление
совершится нацело и
поэтому процесс остановится.
и т. д. Так как степени остатков все
время понижаются, то в этой цепочке
последовательных делений мы должны
дойти до такого места, на котором деление
совершится нацело и
поэтому процесс остановится.
ТЕОРЕМА 8. Тот
остаток
![]() ,
на который нацело делится предыдущий
остаток
,
на который нацело делится предыдущий
остаток![]() ,
ибудет
наибольшим общим делителем многочленов
,
ибудет
наибольшим общим делителем многочленов
![]() и
и
![]() .
.
ДОКАЗАТЕЛЬСТВО. Для доказательства запишем изложенное в предыдущем абзаце в виде следующей цепочки равенств:
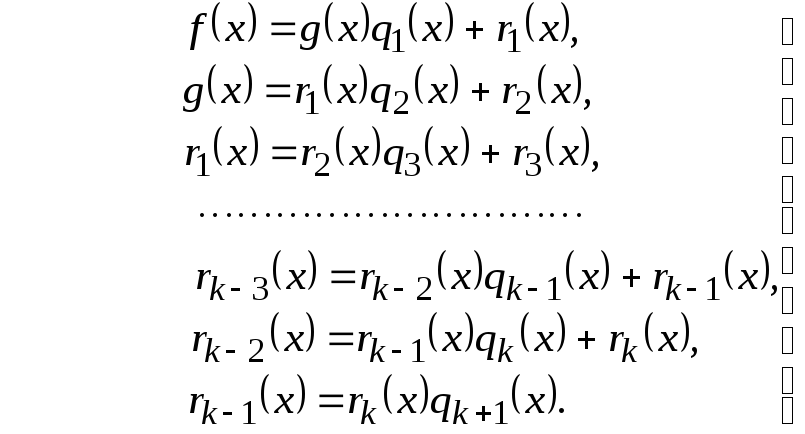 (4)
(4)
Последнее
равенство показывает, что
![]() служит делителем для
служит делителем для![]() .Отсюда
следует, что оба слагаемых правой части
предпоследнего
равенства делятся на
.Отсюда
следует, что оба слагаемых правой части
предпоследнего
равенства делятся на
![]() ,а
поэтому
,а
поэтому
![]() будет
делителем и
для
будет
делителем и
для
![]() .
Далее,
таким же путем, поднимаясь вверх,
получим,
что
.
Далее,
таким же путем, поднимаясь вверх,
получим,
что
![]() является
делителем и для
является
делителем и для
![]() .Отсюда,
ввиду второго равенства, будет следовать,
что
.Отсюда,
ввиду второго равенства, будет следовать,
что
![]() служит
делителем
для
служит
делителем
для
![]() ,а
поэтому, на основании первого равенства,
и
для
,а
поэтому, на основании первого равенства,
и
для
![]() .
Таким
образом,
.
Таким
образом,
![]() является общим делителем для
является общим делителем для
![]() и
и![]() .
.
Возьмем
теперь произвольный общий делитель
![]() многочленов
многочленов
![]() и
и![]() .
Так
как левая часть и первое слагаемое
правой части первого
из равенств (4) делятся на
.
Так
как левая часть и первое слагаемое
правой части первого
из равенств (4) делятся на
![]() ,
то
,
то
![]() также
будет делиться
на
также
будет делиться
на
![]() .
Переходя
ко второму и следующему равенствам, мы
таким же способом получим, что на
.
Переходя
ко второму и следующему равенствам, мы
таким же способом получим, что на
![]() делятся
многочлены
делятся
многочлены
![]() Наконец,
если уже будет доказано, что
Наконец,
если уже будет доказано, что
![]() и
и
![]() делятся
на
делятся
на
![]() ,
то
из предпоследнего равенства мы получим,
что
,
то
из предпоследнего равенства мы получим,
что
![]() делится
на
делится
на
![]() .
Таким образом,
.
Таким образом,
![]() на
самом деле будет наибольшим общим
делителем для
на
самом деле будет наибольшим общим
делителем для
![]() и
и![]() .
□
.
□
Мы
доказали, следовательно, что любые два
многочлена обладают наибольшим
общим делителем, и получили способ для
его вычисления. Этот
способ показывает, что если
многочлены
![]() и
и
![]() имеют оба
рациональные или действительные
коэффициенты, то и коэффициенты
их наибольшего общего делителя также
будут рациональными
или, соответственно, действительными.
имеют оба
рациональные или действительные
коэффициенты, то и коэффициенты
их наибольшего общего делителя также
будут рациональными
или, соответственно, действительными.
Если
![]() есть
наибольший общий делитель многочленов
есть
наибольший общий делитель многочленов
![]() и
и![]() ,
то,
как показывают свойства 8 и 9, в качестве
наибольшего
общего делителя этих многочленов можно
было бы выбрать
также многочлен
,
то,
как показывают свойства 8 и 9, в качестве
наибольшего
общего делителя этих многочленов можно
было бы выбрать
также многочлен
![]() ,где
,где
![]() произвольное число, отличноеот
нуля. Иными словами, наибольший
общий делитель двух многочленов
определен лишь с точностью до множителя
нулевой степени.
Ввиду
этого можно условиться, что
старший коэффициент наибольшего
общего делителя двух многочленов будет
всегда считаться равным единице.
Используя это условие, можно сказать,
что
два
многочлена тогда и
только тогда взаимно просты, когда их
наибольший общий делитель
равен единице.
произвольное число, отличноеот
нуля. Иными словами, наибольший
общий делитель двух многочленов
определен лишь с точностью до множителя
нулевой степени.
Ввиду
этого можно условиться, что
старший коэффициент наибольшего
общего делителя двух многочленов будет
всегда считаться равным единице.
Используя это условие, можно сказать,
что
два
многочлена тогда и
только тогда взаимно просты, когда их
наибольший общий делитель
равен единице.
Пример 11. Найти наибольший общий делитель многочленов:
![]()
Решение. Применяя алгоритм Евклида к многочленам с целыми коэффициентами, мы можем, чтобы избежать дробных коэффициентов, умножить делимое или сократить делитель на любое не равное нулю число, причём, не только начиная какое-либо из последовательных делений, но и в процессе самого этого деления. Это будет приводить, понятно, к искажению частного, но интересующие нас остатки будут приобретать лишь некоторый множитель нулевой степени, что, как мы знаем, при разыскании наибольшего общего делителя допускается.
Делим
![]() на
на![]() ,
предварительно умножив
,
предварительно умножив![]() на 3:
на 3:
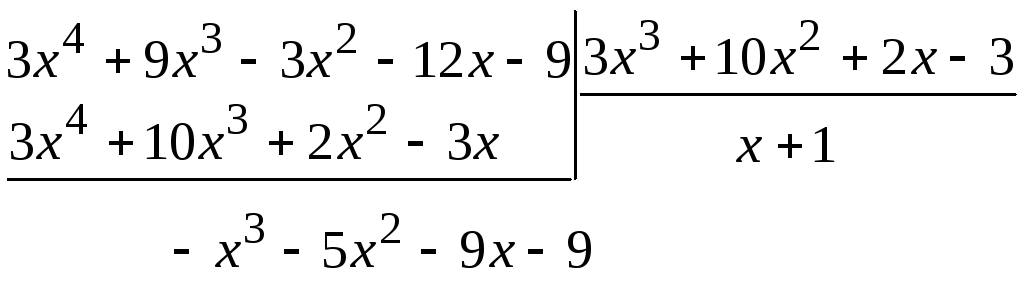
(умножаем на 3)
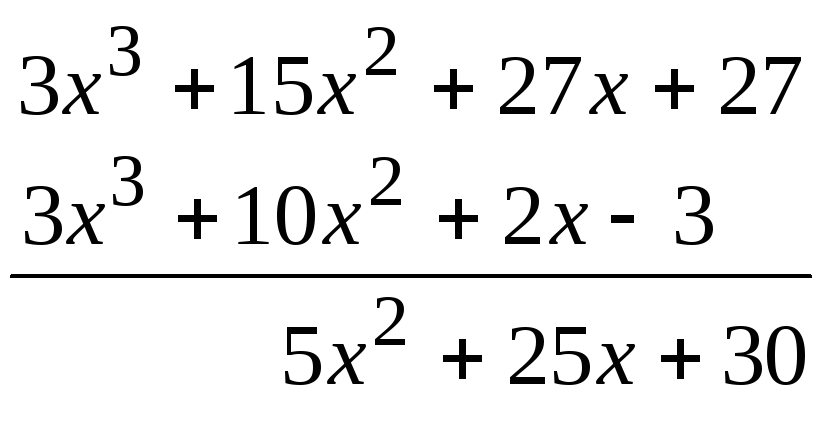
Степень
остатка стала меньше степени делителя,
таким образом, после сокращения на 5
получим первый остаток
![]() .
Делим на него многочлен
.
Делим на него многочлен![]() :
:

Вторым
остатком, после сокращения на 9, будет
![]() .
Очевидно, что
.
Очевидно, что![]() ,
т. е. последним остатком, отличным от
нуля будет
,
т. е. последним остатком, отличным от
нуля будет![]() .
Он и будет искомым наибольшим делителем:
.
Он и будет искомым наибольшим делителем:
![]()
Используем алгоритм Евклида для доказательства следующей теоремы:
ТЕОРЕМА 9. Если
![]() есть наибольший общий делитель
многочленов
есть наибольший общий делитель
многочленов
![]() и
и
![]() ,
то можно найти такие многочлены
,
то можно найти такие многочлены
![]() и
и
![]() ,что
,что
![]() (3)
(3)
Можно
считать при этом, если степени многочленов
![]() и
и
![]() больше
нуля, что степень
больше
нуля, что степень
![]() меньше степени
меньше степени
![]() ,
а степень
,
а степень
![]() меньше степени
меньше степени
![]() .
.
ДОКАЗАТЕЛЬСТВО.
Воспользуемся равенствами (4). Если мы
учтем, что
![]() ,
и
положим
,
и
положим
![]() ,
то
предпоследнее
из равенств (4) даст:
,
то
предпоследнее
из равенств (4) даст:
![]() .
.
Подставляя
сюда выражение
![]() через
через
![]() и
и
![]() из
предшествующего
равенства (4), мы получим;
из
предшествующего
равенства (4), мы получим;
![]() ,
,
где,
очевидно,
![]() .Продолжая
подниматься вверх по равенствам (4), мы
придем, наконец, к доказываемому
равенству (5).
.Продолжая
подниматься вверх по равенствам (4), мы
придем, наконец, к доказываемому
равенству (5).
Дли
доказательства второго утверждения
теоремы предположим, что
многочлены
![]() и
и
![]() ,
удовлетворяющие
равенству (5), уже найдены, но, например,
степень
,
удовлетворяющие
равенству (5), уже найдены, но, например,
степень
![]() больше или равна степени
больше или равна степени
![]() .
Делим
.
Делим
![]() на
на
![]() :
:
![]() ,
,
где степень
![]() меньше степени
меньше степени
![]() ,
и подставляем это выражение в(5).
Получим равенство
,
и подставляем это выражение в(5).
Получим равенство
![]() .
.
Степень
множителя, стоящего при
![]() ,
уже меньше степени
,
уже меньше степени
![]() .Степень
многочлена, стоящего в квадратных
скобках, будет в свою очередь
меньше степени
.Степень
многочлена, стоящего в квадратных
скобках, будет в свою очередь
меньше степени
![]() ,так
как в противном случае степень второго
слагаемого левой части была бы не меньше
степени произведения
,так
как в противном случае степень второго
слагаемого левой части была бы не меньше
степени произведения
![]() ,
а так как степень первого слагаемого
меньшестепени
этого произведения, то вся левая часть
имела бы степень, большую
или равную степени
,
а так как степень первого слагаемого
меньшестепени
этого произведения, то вся левая часть
имела бы степень, большую
или равную степени
![]() ,тогда
как многочлен
,тогда
как многочлен
![]() заведомо
имеет, при наших предположениях, меньшую
степень. □
заведомо
имеет, при наших предположениях, меньшую
степень. □
Одновременно
мы получаем, что если многочлены
![]() и
и![]() имеют
рациональные или действительные
коэффициенты,
то и многочлены
имеют
рациональные или действительные
коэффициенты,
то и многочлены
![]() и
и
![]() ,
удовлетворяющие
равенству
(5), можно подобрать так, что их коэффициенты
будут рациональными
или, соответственно, действительными.
,
удовлетворяющие
равенству
(5), можно подобрать так, что их коэффициенты
будут рациональными
или, соответственно, действительными.
Пример 12.
Найти многочлены
![]() и
и![]() ,
удовлетворяющие равенству (3) при
,
удовлетворяющие равенству (3) при![]()
Решение.
Применим к этим многочленам алгоритм
Евклида, причём теперь при выполнении
делений уже нельзя допускать искажения
частных, так как эти частные используются
при разыскании многочленов
![]() и
и![]() .
Получим такую систему равенств:
.
Получим такую систему равенств:
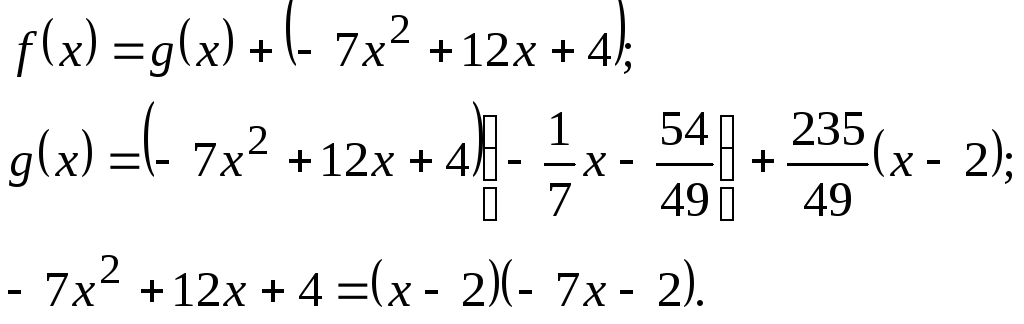
Отсюда следует,
что
![]() и что
и что
![]()
СЛЕДСТВИЕ
4. Многочлены
![]() и
и
![]() тогда и только тогда взаимно просты,
если
можно найти многочлены
тогда и только тогда взаимно просты,
если
можно найти многочлены
![]() и
и
![]() ,
удовлетворяющие равенству
,
удовлетворяющие равенству
![]()
Опираясь на этот результат, можно доказать несколько простых, но важных утверждений о взаимно простых многочленах:
УТВЕРЖДЕНИЕ
1. Если
многочлен
![]() взаимно прост с каждым из многочленов
взаимно прост с каждым из многочленов
![]() и
и![]() ,
то он взаимно прост и с их произведением.
,
то он взаимно прост и с их произведением.
ДОКАЗАТЕЛЬСТВО.
В
самом деле, по предыдущему следствию,
существуют такие многочлены
![]() и
и
![]() ,
что
,
что
![]()
Умножая
это равенство на
![]() ,
получаем:
,
получаем:
![]() ,
,
откуда
следует, что всякий общий делитель
![]() и
и
![]() был бы делителем
и для
был бы делителем
и для
![]() ,
однако
по условию
,
однако
по условию
![]() .
□
.
□
УТВЕРЖДЕНИЕ
2. Если
произведение многочленов
![]() и
и
![]() делится на
делится на
![]() ,но
,но
![]() и
и
![]() взаимно просты, то
взаимно просты, то
![]() делится на
делится на
![]() .
.
ДОКАЗАТЕЛЬСТВО.
Умножим
равенство
![]() на
на
![]() ,
получим:
,
получим:
![]() .
.
Оба
слагаемых левой части этого равенства
делятся на
![]() ;
на него делится,
следовательно, и
;
на него делится,
следовательно, и
![]() .
□
.
□
УТВЕРЖДЕНИЕ
3. Если
многочлен
![]() делится на каждый из многочленов
делится на каждый из многочленов
![]() и
и![]() ,
которые между собой взаимно просты, то
,
которые между собой взаимно просты, то
![]() делится
и на их произведение.
делится
и на их произведение.
ДОКАЗАТЕЛЬСТВО.
Действительно,
![]() ,
так что произведение, стоящеесправа,
делится на
,
так что произведение, стоящеесправа,
делится на
![]() .
Поэтому,
по утверждению 2,
.
Поэтому,
по утверждению 2,
![]() делится на
делится на
![]() ,
,
![]() ,откуда
,откуда
![]() .
□
.
□
Определение
наибольшего общего делителя может быть
распространено
на случай любой конечной системы
многочленов: наибольшим
общим
делителем многочленов
![]() называется такой общий делитель этих
многочленов, который делится на любойдругой
общий делитель этих многочленов.
Существование наибольшего общего
делителя для любой конечной системы
многочленов вытекает из следующей
теоремы, дающей также способ его
вычисления.
называется такой общий делитель этих
многочленов, который делится на любойдругой
общий делитель этих многочленов.
Существование наибольшего общего
делителя для любой конечной системы
многочленов вытекает из следующей
теоремы, дающей также способ его
вычисления.
ТЕОРЕМА 10. Наибольший
общий делитель многочленов
![]() равен
наибольшему общему делителю многочлена
равен
наибольшему общему делителю многочлена
![]() и наибольшего
общего делителя многочленов
и наибольшего
общего делителя многочленов
![]() .
.
ДОКАЗАТЕЛЬСТВО.
В самом деле, при
![]() теорема очевидна. Пусть она справедлива
для случая
теорема очевидна. Пусть она справедлива
для случая![]() ,
т. е., в частности, уже доказано
существование наибольшего общего
делителя
,
т. е., в частности, уже доказано
существование наибольшего общего
делителя![]() многочленов
многочленов![]() .
Обозначим через
.
Обозначим через![]() наибольший общий делитель многочленов
наибольший общий делитель многочленов![]() и
и![]() .
Он будет, очевидно, общим делителем для
всех заданных многочленов. С другой
стороны, всякий другой общий делитель
этих многочленов будет делителем также
и для
.
Он будет, очевидно, общим делителем для
всех заданных многочленов. С другой
стороны, всякий другой общий делитель
этих многочленов будет делителем также
и для![]() ,
а поэтому и для
,
а поэтому и для![]() .
.
В
частности, система многочленов
![]() называетсявзаимно
простой,
если общими делителями этих многочленов
являются лишь многочлены нулевой
степени, т. е. если их наибольший общий
делитель
равен 1.
□
называетсявзаимно
простой,
если общими делителями этих многочленов
являются лишь многочлены нулевой
степени, т. е. если их наибольший общий
делитель
равен 1.
□
ЗАДАЧИ К ГЛАВЕ IV.
Вычислить выражения:
133.
![]()
134.
![]()
135.
![]()
136.
![]()
137.
![]()
138.
![]()
139.
![]()
140.
![]()
141.
![]()
142.
![]()
143.
![]()
144.
![]()
145.
Вычислить
![]()
Решить уравнения:
146.
![]()
147.
![]()
148.
![]()
149.
![]()
150.
![]()
151.
![]()
Найти тригонометрическую форму комплексных чисел:
152.
![]()
153.
![]()
154.
![]()
155.
![]()
156.
![]()
157.
![]()
158.
![]()
159.
![]()
160.
![]()
161.
![]()
162.
![]()
163.
![]()
164.
![]()
165.
![]()
166.
![]()
167.
![]()
Вычислить выражения:
168.
![]()
169.
![]()
170.
![]()
171.
![]()
172.
![]()
173.
![]()
174.
![]()
175.
![]()
Решить уравнения:
176.
![]()
177.
![]()
При
![]() вычислить выражения:
вычислить выражения:
178.
![]()
179.
![]()
180. Доказать,
что если комплексное число
![]() является одним из корней степени
является одним из корней степени![]() из вещественного числа
из вещественного числа![]() ,
то и сопряжённое число
,
то и сопряжённое число![]() является одним из корней степени
является одним из корней степени![]() из
из![]() .
.
Вычислить:
181.
![]()
182.
![]()
183.
![]()
184.
![]()
185.
![]()
186.
![]()
187.
![]()
188.
![]()
189.
![]()
190.
![]()
191.
![]()
192.
![]()
193.
![]()
194.
![]()
195.
![]()
196.
![]()
197.
![]()
198.
![]()
199.
![]()
Решить уравнения:
200.
![]()
201.
![]()
202.
![]()
203.
Найти произведение всех корней степени
![]() из единицы.
из единицы.
Используя
алгоритм Евклида, Разделить многочлен
![]() с остатком на многочлен
с остатком на многочлен![]() :
:
204.
![]()
205.
![]()
Найти
наибольший общий делитель многочленов
![]() и
и![]() :
:
206.
![]()
207.
![]()
208.
![]()
209.
![]()
210.
![]()
211.
![]()
212.
![]()
213.
![]()
214.
![]()
215.
![]()
216.
![]()
Найти
наибольший общий делитель многочленов
![]() и
и![]() и его линейное выражение через
и его линейное выражение через![]() и
и![]() :
:
217.
![]()
218.
![]()
ОТВЕТЫ.
1.
![]()
2.
![]()
3.
![]()
4.
5.
6.
7.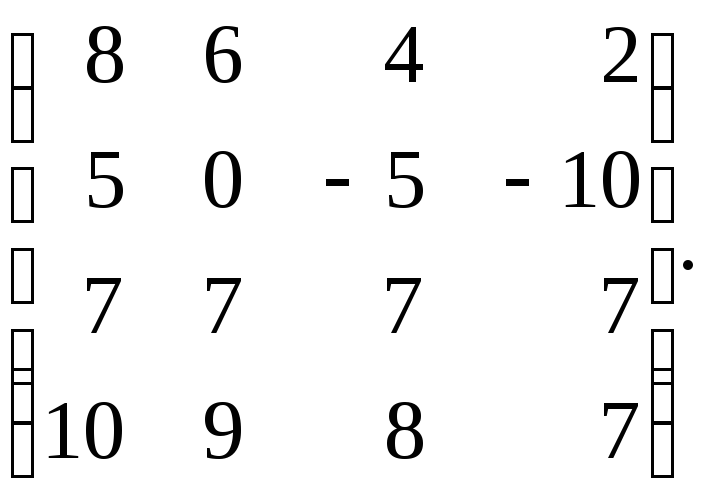
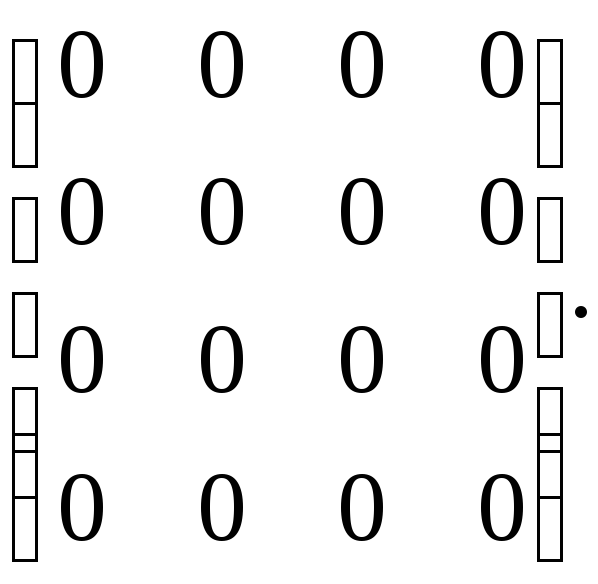
8.
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14. 1.
15. -2.
16. 0.
17. 0.
18.
![]()
19 .![]()
20. 0.
21. 0.
22. 1.
23. 40.
24. -10.
25. 180.
26. 87.
27. 0.
28. 10.
29. -8.
30. -3.
31. -9.
32. 18.
33. 18.
34. 17.
35. -6.
36. -10.
37. 100.
38. 150.
39. 52.
40. 5.
41. 10.
42. 1.
43.
![]()
44.
![]()
45. 0.
46.
![]()
47.
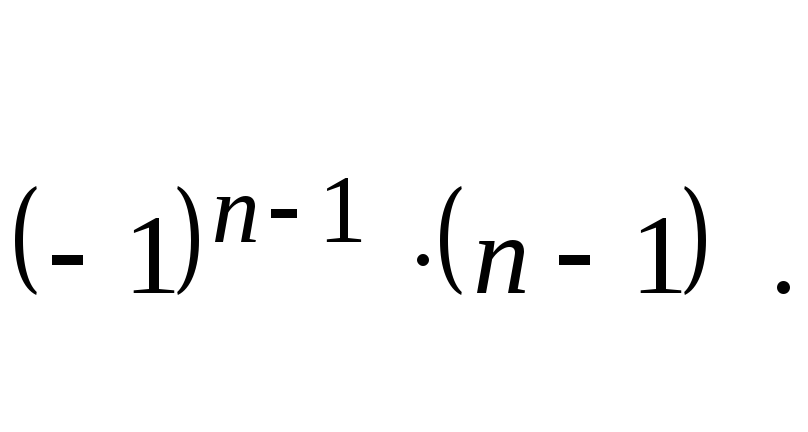
48.
![]()
49.
![]()
50.
![]()
51.
![]()
52.
![]()
53.
![]()
54.
![]()
55.
![]()
56.
![]()
57.
![]()
58.
![]()
59.
![]()
60.
![]()
61.
![]()
62.
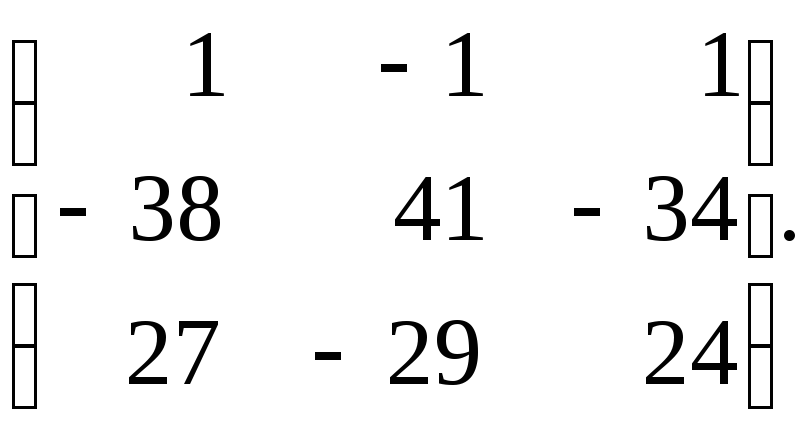
63.
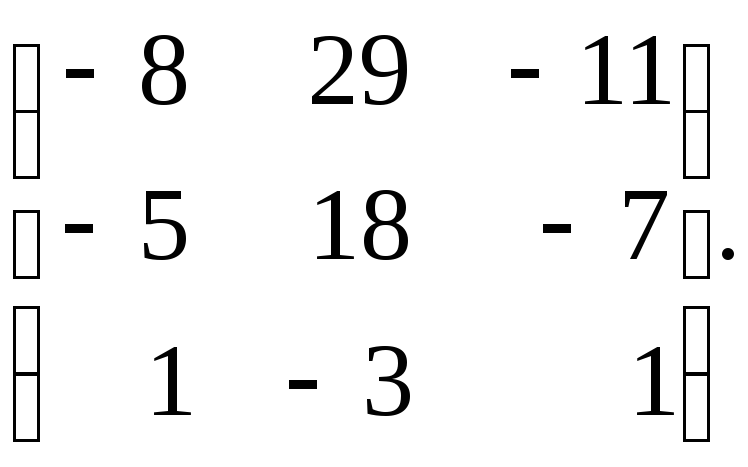
64.
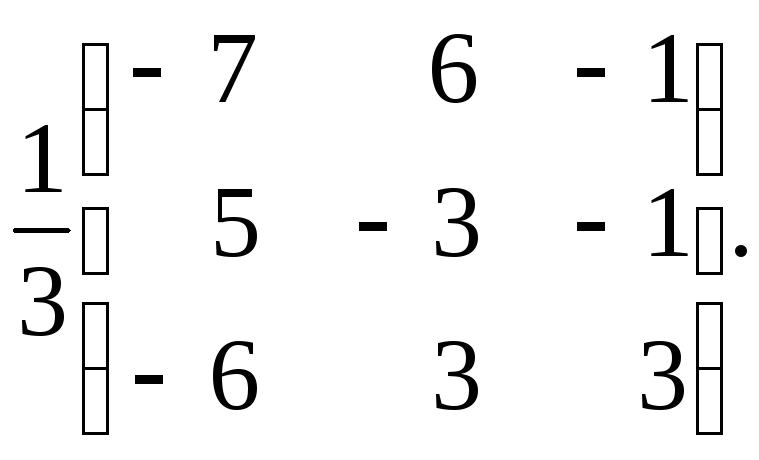
65.
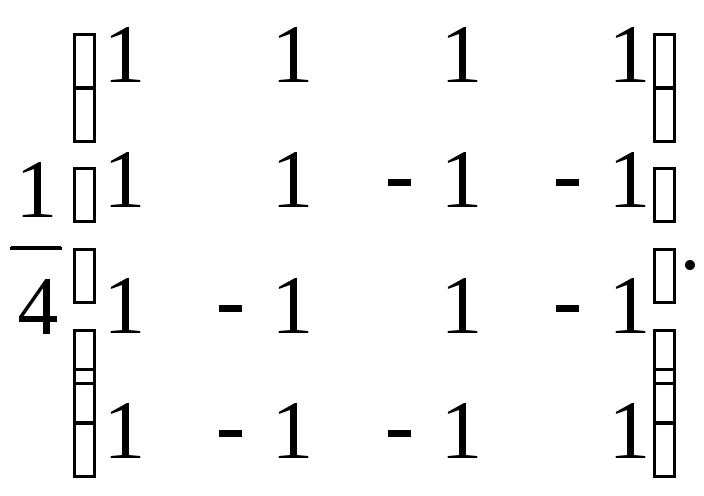
66.

67.

68.

69.
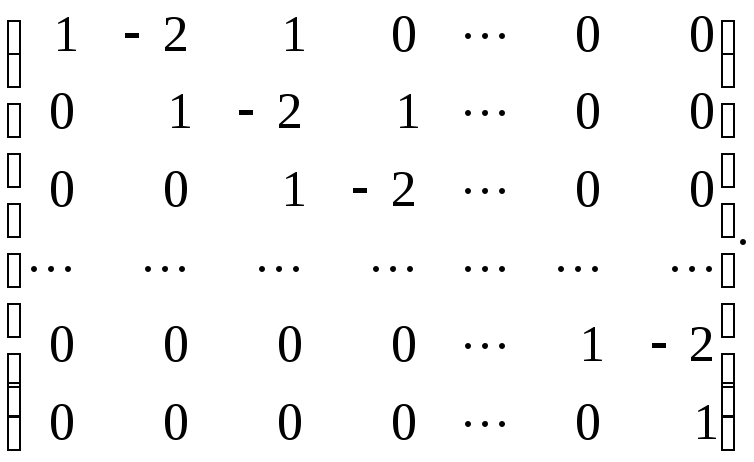
70.

71.
![]()
72.
![]()
73.
![]()
74.

75.
76.
77.

78. 2.
79. 3.
80. 3.
81. 2.
82. 2.
83. 2.
84. 3.
85. 3.
86. 2.
87. При
![]() ранг матрицы равен 2, при
ранг матрицы равен 2, при![]() ранг равен 3.
ранг равен 3.
88. При
![]() ранг матрицы равен 2, при
ранг матрицы равен 2, при![]() ранг равен 3.
ранг равен 3.
89. Общее решение, например:
![]() ,
,
![]() ;
частное решение:
;
частное решение:![]()
90. Общее решение:
![]() ,
,
![]() ;
частное решение:
;
частное решение:![]()
91. Общее решение:
![]() ,
,
![]() ;
частное решение:
;
частное решение:![]()
92. Общее решение:
![]() ;
частное решение:
;
частное решение:![]()
93. Система несовместна.
94. Система имеет
единственное решение:
![]()
95. Система несовместна.
96. Общее
решение:
![]() частное решение:
частное решение:![]()
97. Общее
решение:
![]() частное решение:
частное решение:![]()
98. Система имеет единственное решение:
![]()
99. Система несовместна.
100. При
![]() система несовместна. При
система несовместна. При![]() она совместна, и общее решение имеет
вид:
она совместна, и общее решение имеет
вид:![]()
101. Система
совместна при любых значениях
![]() .
При
.
При![]() общее решение имеет вид:
общее решение имеет вид:![]() При
При![]() общее решение имеет вид:
общее решение имеет вид:![]()
102. Общее
решение, например:
![]() ,
,![]() .
Фундаментальная система решений:
.
Фундаментальная система решений:
|
|
|
|
|
|
8 |
-6 |
1 |
0 |
|
-7 |
5 |
0 |
1 |
103. Общее
решение:
![]() Фундаментальная система решений:
Фундаментальная система решений:
|
|
|
|
|
|
1 |
0 |
|
|
|
0 |
1 |
5 |
7 |
104. Система имеет только нулевое решение.
105. Система имеет только нулевое решение.
106. Общее
решение:
![]() Фундаментальная система решений:
Фундаментальная система решений:
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
0 |
|
-1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
-1 |
0 |
0 |
0 |
1 |
107. Общее
решение:
![]() Фундаментальная система решений:
Фундаментальная система решений:
|
|
|
|
|
|
|
0 |
|
1 |
0 |
0 |
|
0 |
|
0 |
0 |
1 |
108. Общее
решение:
![]() Фундаментальная система решений:
Фундаментальная система решений:
|
|
|
|
|
|
|
-3 |
2 |
1 |
0 |
0 |
|
-5 |
3 |
0 |
0 |
1 |
109. Четвёртая строка вместе с любыми двумя из первых трёх строк образуют фундаментальную систему, а остальные системы строк не образуют.
110.
![]()
111.
![]()
112.
![]()
113.
![]()
114.
![]()
115.
![]()
116.

117.

118.
119.
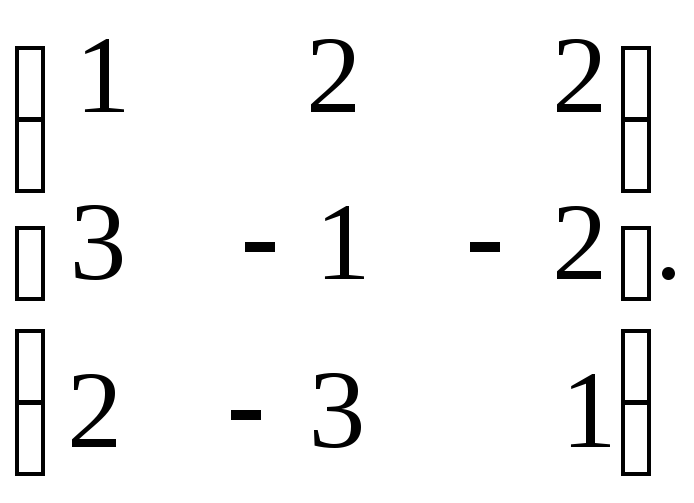
120. а)

б)

121. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]()
![]()
![]() где
где![]()
122. Собственные
значения:
![]() Собственные векторы имеют вид:
Собственные векторы имеют вид:![]() где
где![]()
123. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]()
![]()
![]() где
где![]()
124. Собственные
значения:
![]() Собственные векторы имеют вид:
Собственные векторы имеют вид:![]() где
где![]() и
и![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
125. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]()
![]() где
где![]()
126. Собственные
значения:
![]() Собственные векторы имеют вид:
Собственные векторы имеют вид:![]() где
где![]()
127. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]()
![]() где
где![]()
128. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]() ,
где
,
где![]()
![]() где
где![]() и
и![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
129. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]() ,
где
,
где![]()
![]() где
где![]() и
и![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
130. Собственные
значения:
![]() Соответствующие собственные векторы:
Соответствующие собственные векторы:![]() ,
где
,
где![]() и
и![]() и
и![]() не равны нулю одновременно;
не равны нулю одновременно;![]() где
где![]() и
и![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
131. Собственные
значения:
![]() Собственные векторы имеют вид:
Собственные векторы имеют вид:![]() где
где![]() и
и![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
132. Собственные
значения:
![]() Собственные векторы имеют вид:
Собственные векторы имеют вид:![]() где
где![]() и
и![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
133.
![]()
134.
![]()
135.
![]()
136.
![]()
137.
![]()
138.
![]()
139.
![]()
140.
![]()
141.
![]()
142.
![]()
143.
![]()
144.
![]()
145. ![]() при
при![]() ,
,![]() при
при![]() ,
,![]() при
при![]() ,
,![]() при
при![]() ,
где
,
где![]() целое
число;
целое
число;![]()
146.
![]()
147.
![]()
148.
![]()
149.
![]()
150.
![]()
151.
![]()
152.
![]()
153.
![]()
154.
![]()
155.
![]()
156.
![]()
157.
![]()
158.
![]()
159.
![]()
160.
![]()
161.
![]()
162.
![]()
163.
![]()
164.
![]()
165.
![]()
166.
![]()
167.
![]()
168.
![]()
169.
![]()
170.
![]()
171.
![]()
172.
![]()
173.
![]()
174.
![]()
175.
![]()
176.
![]()
177.
![]()
181.
![]()
182.
![]()
183.
![]()
184.
![]()
185.
![]()
186.
![]()
187.
![]()
188.
![]()
189.
![]()
190.
![]()
191.
![]()
192.
![]()
193.
![]()
194.
![]()
195.
![]()
196.
![]()
197.
![]()
198.
![]()
199.
![]()
203.
![]()
204.
![]()
205.
![]()
206.
![]()
207.
![]()
208.
![]()
209.
![]()
210.
![]()
211.
![]()
212.
![]()
213.
![]()
214.
![]()
215.
![]()
216.
![]()
217.
![]()
218.
![]()
СПИСОК ЛИТЕРАТУРЫ.
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб.: Для ВУЗов. М.: Физматлит, 2001.
Курош А. Г. Курс высшей алгебры. М.: Наука, 1971.
Проскуряков И. В. Сборник задач по линейной алгебре. М.: Наука, 1984.
Шипачёв В. С. Задачник повысшей математике: Учеб. пособие для ВУЗов. М.: Высшая школа, 2002.
СОДЕРЖАНИЕ.
ВВЕДЕНИЕ. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ. 3
