§2.2. Ранг матриц.

Наивысший порядок минора матрицы, неравного нулю, называется минорным рангом матрицы.

Будем смотреть на столбцы, впрочем, как и на строки, матрицы как на векторы пространства(соответственно,). Говорят, что подмножество векторовлинейного пространства является егоподпространством, если для всех и числавыполнены два условия:

(а);

(б).

Их можно объединить в одно: для любых и чиселвектор. В этом случае нетрудно проверить выполнение всех свойств 1-8 сложения и умножения числа на вектор из § 2.1. Поэтому подпространства в свою очередь являются пространствами, т.к. условия 1-8 фактически являются аксиомами «быть пространством» для множества элементов, в котором заданы операции сложения и умножения числа на элемент из.

Универсальным способом получения подпространств является следующий: надо взять произвольное множество векторов из пространства и тогда, как не трудно проверить, множествовсевозможных линейных комбинаций векторов изобразует подпространство исходного линейного пространства, о котором говорят, что оно порождено векторами. По теореме о базисах любая максимальная линейная независимая система векторов изсодержит одно и то же число векторов. Поэтому корректно следующее определение: число столбцов, образующих в матрице максимальную линейно независимую систему, называетсярангом матрицы по столбцам. Аналогично определяется и ранг матрицы по строкам.

ТЕОРЕМА (о ранге матриц). Ранг матрицы по столбцам равен ее минорному рангу.

ДОКАЗАТЕЛЬСТВО. Если в матрице любые столбцов линейно зависимы, то, по свойству 8 определителя, любой минорпорядка равен нулю. Поэтому минорный ранг не больше ранга по столбцам.

Обратно, пусть минорный ранг матрицы порядкаравен. Так как при расстановке строк и столбцов матрицы ее ранг не меняется, то можно считать, что минорпорядка, не равный, находится на пересечении первыхстолбцов и строк. Рассмотрим«окаймляющий» его минор.

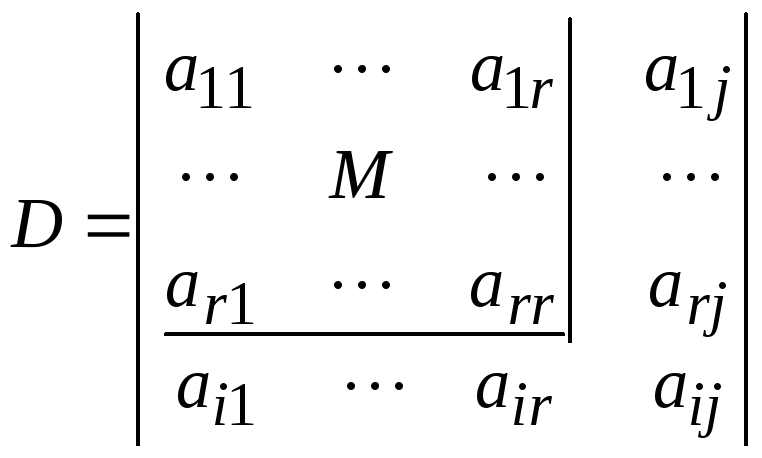
Здесь . Если, тосодержит две равные строки и, по свойству 4 определителей, равен. Если же, томинорпорядка и равенпо предположению. Вычислим методом разложения по последней строке:

(6)

Заметим, что ,не зависят от. Из равенства (6) получаем:

Это равенство справедливо при любом . Поэтомустолбец исходной матрицы равен линейной комбинации ее первыхстолбцов, взятых с коэффициентами:

Итак, первые столбцов образуют максимальную линейную независимую систему столбцов. Значит ранг по столбцам не выше минорного ранга, что заканчивает доказательство теоремы. □

Так как при транспонировании матрицы ее минорный ранг не меняется, то получаем:

СЛЕДСТВИЕ  5. Ранг матрицы по строкам равен ее рангу по столбцам. □

СЛЕДСТВИЕ  6. Квадратная матрица является невырожденной тогда и только тогда, когда ее строки (столбцы) образуют линейно независимую систему строк (столбцов). □

Доказательство теоремы о ранге дает и метод вычисления ранга матрицы. Именно, найдя минор порядка, не равный, надо перебрать все его окаймляющие (в теореме надо брать, ), и, если все они равны , то ранг матрицы равен.

Она дает также и способ нахождения максимальной линейно независимой системы строк (столбцов) матрицы. Именно, это будут те строки (столбцы), в которых лежит минор наивысшего порядка, не равный нулю.

Пример 1. Найти ранг матрицы

.

Решение. Минор второго порядка, стоящий в левом верхнем углу этой матрицы отличен от нуля.

Минор третьего порядка

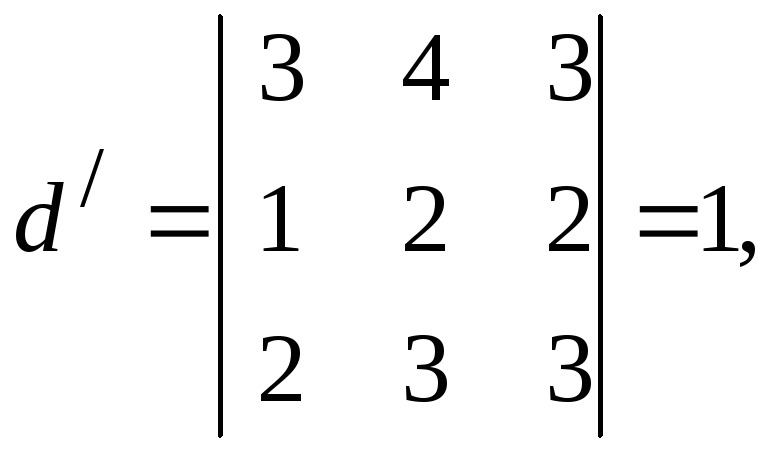
окаймляющий , отличен от нуля, однако оба минора четвёртого порядка, окаймляющие, равны нулю:

т. е. ранг матрицы равен трём.

Назовём элементарными следующие преобразования матриц:

• перестановка строк (столбцов);

• домножение строки (столбца) на число, отличное от нуля;

• добавление к одной строке (столбцу) другой строки (столбца), умноженной на некоторое число;

• вычёркивание нулевой строки (столбца).

УТВЕРЖДЕНИЕ 1. Элементарные преобразования не меняют ранга матрицы. □

УТВЕРЖДЕНИЕ 2. Система из векторов

линейно независима. □

В заключении укажем ещё один алгоритм нахождения ранга матриц, основанный на утв. 1, 2: с помощью элементарных преобразований приведём матрицу к ступенчатому виду; количество её строк и будет рангом матрицы.

Пример 2. Найти ранг матрицы

.

Решение. Домножим первую строку матрицы на (-2), (-3), (-1) и прибавим, соответственно, ко второй, третьей и четвёртой строкам, получим

Теперь домножим вторую строку матрицы на (-1) и прибавим к третьей и четвёртой строкам. Вычеркнув нулевую строку, получим матрицу

ступенчатого вида, у которой три строки. Т. е. ранг матрицы равен трём.