§4.2. Поле комплексных чисел.

На протяжении изучения предмета математики неоднократно происходит обогащение понятия числа. На первом этапе школьник, изучающий математику, сталкивается с натуральными числами . С введением отрицательных чисел, появляется возможность рассмотрения системы целых чисел, состоящей из натуральных чисел, противоположных натуральным и нуля. Следующая, более широкая система рациональных чисел, состоящая из всех целых чисел и всех дробных, как положительных, так и отрицательных. Дальнейшее расширение понятия числа происходит тогда, когда в рассмотрение вводятся иррациональные числа. Система, состоящая из всех рациональных и всех иррациональных чисел, называется системой действительных (или вещественных) чисел. Комплексные числа вводятся в связи со следующей задачей: нужно расширить систему действительных чисел до такой системы, в которой каждое квадратное уравнение (в частности уравнение) обладало бы корнем.

В качестве материала для построения новой системы чисел возьмём точки плоскости , каждая из которых однозначно определяется упорядоченной парой действительных чисел. Введём операции сложения и умножения для таких элементов следующим образом:

Покажем, что множество с введёнными операциями сложения и умножения образует поле. Очевидно, сложение и умножение являются коммутативными операциями, а сложение, кроме того, ассоциативно. Нейтральным элементом по сложению является пара, по умножению . Для парыпротивоположна пара. В качестве упражнения читателю предлагается доказать ассоциативность умножения и дистрибутивность умножения относительно сложения. Осталось показать, что для каждого ненулевого элемента существует обратный. Для этого решим уравнениеотносительнои. Оно сводится к решению системы двух линейных уравнений с двумя неизвестными:

Данная система совместна для и имеет единственное решение, т. е..

Итак, система 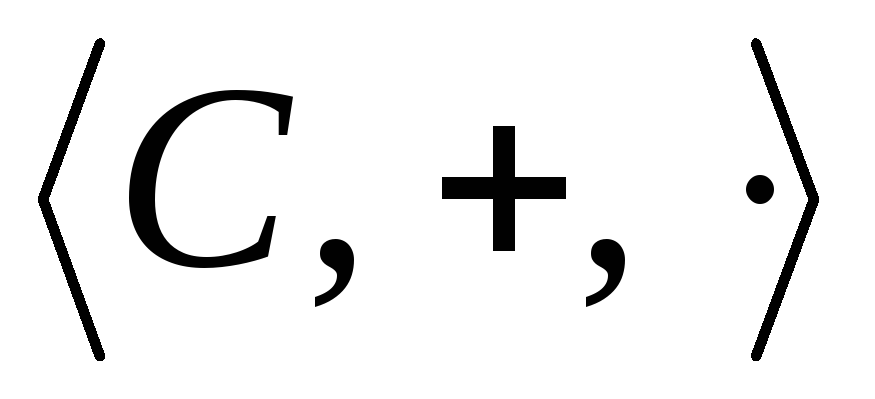является полем и называетсясистемой комплексных чисел.

Покажем теперь, что система комплексных чисел является расширением системы действительных чисел. Для этой цели рассмотрим точки, лежащие на оси абсцисс, т. е. точки вида . Для них справедливо

т. е. они складываются и перемножаются так же, как соответствующие действительные числа. Это позволяет нам в дальнейшем не различать точку и действительное число.

Вернёмся к уравнению . Во множестве комплексных чисел его решением будет, например, точка. Действительно,. Условимся обозначать эту точку буквой, так что. Будем называть комплексное числомнимой единицей. Имеем, . Таким образом,. Следовательно, любое комплексное число можно представить в виде, гденазываетсядействительной частью комплексного числа, а мнимой частью. Плоскость, точки которой отождествлены с комплексными числами, будем называть комплексной плоскостью. Ось абсцисс этой плоскости называется действительной осью, а ось ординат  мнимой осью.

Положение точки на плоскости однозначно задаётся парой действительных чисели. Однако, её положение также вполне определяется с помощью полярных координат, т. е. расстояниемот точки до начала координат и угломмежду положительным направлением оси абсцисс и направлением из начала координат на эту точку. Числоназываетсяабсолютной величиной или модулем комплексного числа, а число аргументом. Очевидно, что абсолютная величина неотрицательна, а аргумент определён с точностью до слагаемых, кратных .

Между декартовыми и полярными координатами существует следующая связь, справедливая при любом расположении точек на плоскости:

Для произвольного комплексного числа имеем:

Эта запись числа называется его тригонометрической формой. Абсолютная величинанаходится по формуле. Аргументможет быть найден из системы уравнений:

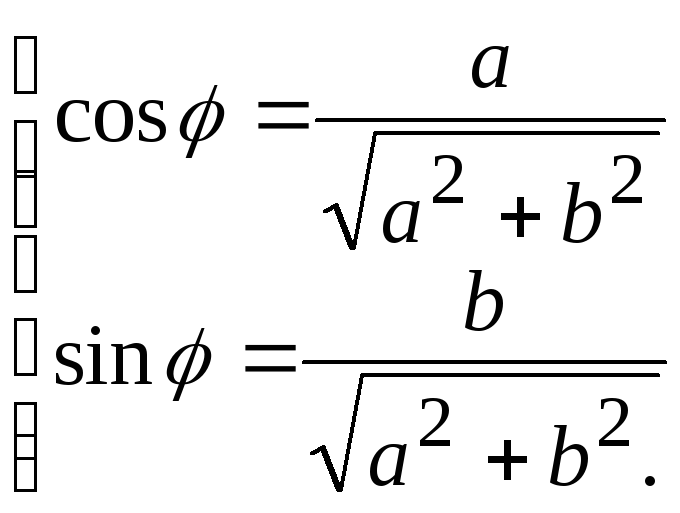
Пример 7. Найти тригонометрическую форму числа .

Р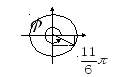ешение. Здесь ,. Тогда.

Решая систему, получаем .Таким образом

Пусть комплексные числа изаданы в тригонометрической форме:,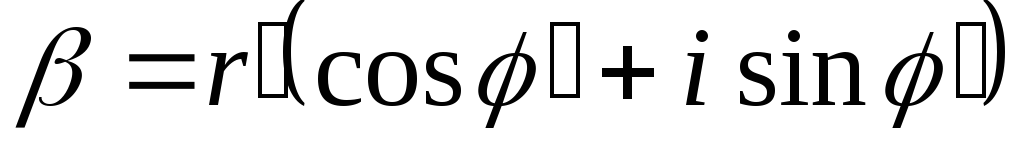. Перемножим эти числа:

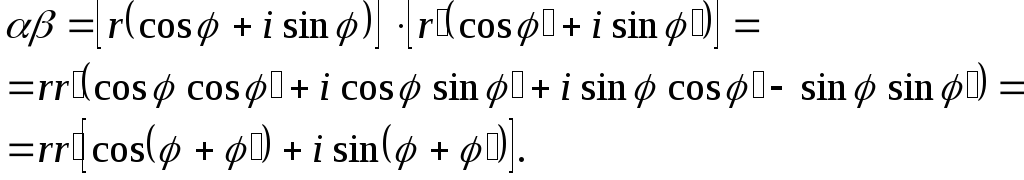
Таким образом, модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей. Аналогичное правило имеет место и для частного. Если , то:

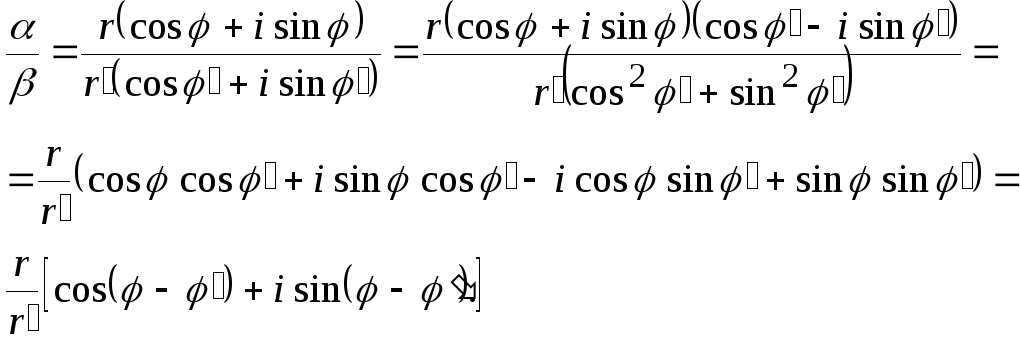
Следовательно, модуль частного двух комплексных чисел равен модулю делимого, делённому на модуль делителя, а аргумент частного получается вычитанием аргумента делителя из аргумента делимого.

Следствием из формулы умножения комплексных чисел является формула Муавра:

Пусть, теперь, нужно извлечь корень степени из числа. Предположим, что это сделать можно и что в результате получается число, т. е.

Тогда  однозначно определённое положительное значение корня ой степени из неотрицательного действительного числа. А аргументыимогут отличаться на слагаемое, кратное, т. е., гдецелое число. Откуда. Таким образом, окончательно имеем:

.

Давая различные значения, мы не всегда будем получать различные значения искомого корня. Действительно, при

получим значений корня, которые все будут различными, так как увеличениена единицу влечёт за собой увеличение аргумента на. Для произвольногоимеем, следовательно

,

т. е. значение аргумента при этом отличается от значения аргумента прина число, кратное. Следовательно, значение корня при произвольномтакое же, как при значении, равном, где.

Таким образом, извлечение корня ой степени из комплексного числавсегда возможно и даётразличных значений. Все значения корняой степени расположены на окружности радиусас центром в нуле и делят эту окружность наравных частей.

Пример 8. Вычислить .

Решение.

Пример 9. Вычислить .

Решение. Найдём тригонометрическую форму числа :

.

Тогда .

При имеем:.

При :.

Пример 10. Вычислить .

Решение. В тригонометрической форме .

.

: ;

: ;

: .