
Z
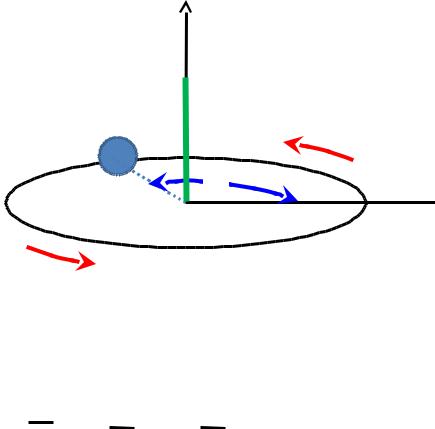
Плоский ротатор
(t) = t
L 
где — угловая скорость (частота вращения), выраженная в радианах/с.
φ
 X
X
Е = —— = ——— = |
|—–L| |
|||
mv |
|
m r |
|
2 |
|
2 |
2 |
2 |
|
2 |
|
2 |
|
2I |
I = mr2 — момент инерции (число) |
||||
L = r mv — момент импульса |
(псевдовектор) |
|
||
LZ = ± |L| — проекция вектора момента на ось Z (число)

Квантовомеханическое описание
Задача: найти все стационарные состояния ротатора; для каждого состояния установить вид волновой функции и допустимые значения наблюдаемых
Φ(φ, t) = ??? E = ??? L = ???
Φ( , t) = D1 1 + D2 2 + . . . + Dr r
Стационарные волновые функции
(собственные функции оператора Гамильтона)
E |
|
i — t |
= ( ) еi t |
( , t) = ( ) е |

2 |
d 2 (x) |
– —— ———– = Е (x) |
|
2m |
dx2 |
(х) = А е ikx + В e–ikx
2 |
d 2 (φ) |
– —— ———– = Е (φ) |
|
2I |
dφ2 |
(φ) = А е imφ + В e–imφ
Поступательное
движение
|P |
k = —–X
Вращательное
движение
|L |
m = —–Z
m — вращательное квантовое число

Граничные условия
(φ)
(φ) = (φ + 2 )
(волновая функция должна воспроизводиться после каждого полного оборота)
( ) = Ae im + Be –im |
Z |
|
( + 2 ) = Ae im( + 2 ) |
+ Be–im( + 2 ) = |
|
= Ae im e im2 + Be –im e –im2 |
Z* |
|
e im2 = e –im2 = 1 |
m = 0, 1, 2, … |
|

Наблюдаемые
| L | = m = 0, , 2 , 3 , . . .
Lz = ± m = 0, ± , ±2 , ±3 , . . .
E = | L |2 / 2I = b m2 = 0, b, 4b, 9b, . . .
(b = 2 / 2I — вращательная постоянная)
Вывод: для ротатора (как и для частицы в ящике) стационарными являются не любые состояния, а только некоторые, выделенные в отношении значений энергии и момента импульса.
Такие состояния образуют дискретное множество и их можно пронумеровать с помощью вращательного квантового числа : m = 0, 1, 2, …
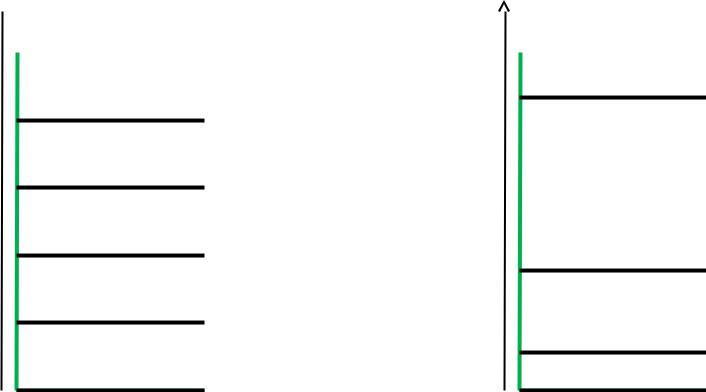
Импульсная
диаграмма
| L | 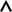
| L | = 4 |
m = 4 |
|
|
| L | = 3 |
m = 3 |
|
|
| L | = 2 |
m = 2 |
|
|
| L | = |
m = 1 |
|
|
| L | = 0 |
m = 0 |
Энергетическая
диаграмма
b = 2 |
/ 2I |
E |
|
m = 3
E = 9b
m = 2
E = 4b
E = b |
m = 1 |
|
m = 0 |
||
E = 0 |
||
|
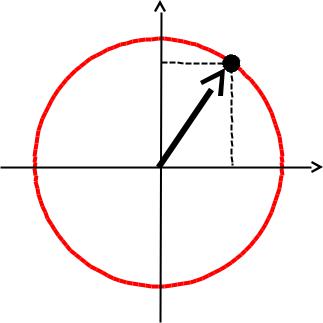
Волновые функции
(φ) = |
А е imφ + |
В e–imφ |
(m = 0,1, 2, … ) |
|
|
На коэффициенты А и В |
|
В |
|
ограничений нет, поэтому каждому |
|
|
разрешенному уровню энергии |
||
В1 |
соответствует двумерное |
||
|
пространство состояний |
||
|
А |
( окружность А2 + В2 = 1 ) |
|
|
Все эти состояния имеют |
||
|
А1 |
||
|
одинаковые значения энергии и |
||
|
|
модуля вектора момента |
|
|
|
E = const |
и | L | = const |
|
|
но различаются по величинам |
|
|
|
коэффциентов А и В |
|
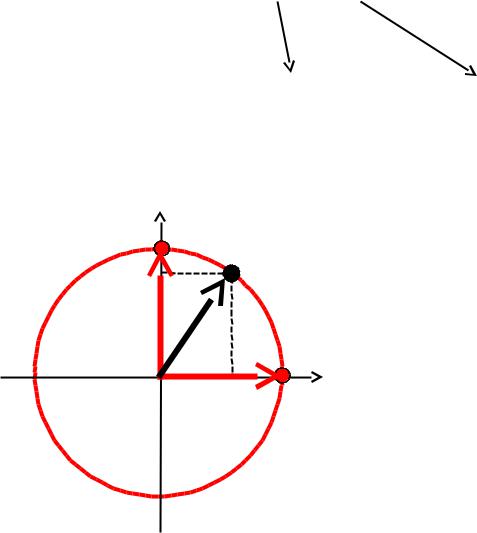
Это пространство удобно описывать, выделяя в нем двумерный базисный набор:
(φ) = С1 + + С2 –
В –
В1 |
+ |
= е imφ |
|
А |
|||
|
= е–imφ |
||
А1 + |
– |

(φ) = А е imφ + В e–imφ
Базисные состояния
Эти базисные состояния отличаются тем, что для них точно известно значение одной из наблюдаемых — проекции LZ
+ = е imφ ( LZ = + | L | )
(частица движется равномерно против часовой стрелки)
– = е –imφ ( LZ = – | L | )
(частица движется равномерно по часовой стрелке)
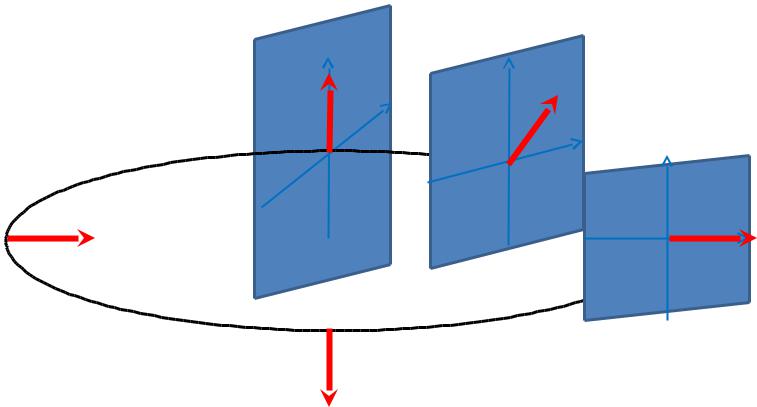
+ = е imφ |
i |
i |
|
|
1 |
1 |
i |
1
Конец стрелки описывает левую спираль вокруг траектории движения (число полных оборотов равно квантовому числу m)
| |
+ |
|2 |
1 |
|
= const = —– |
||
|
|
|
2 |
(движение равномерное и строго направленое)
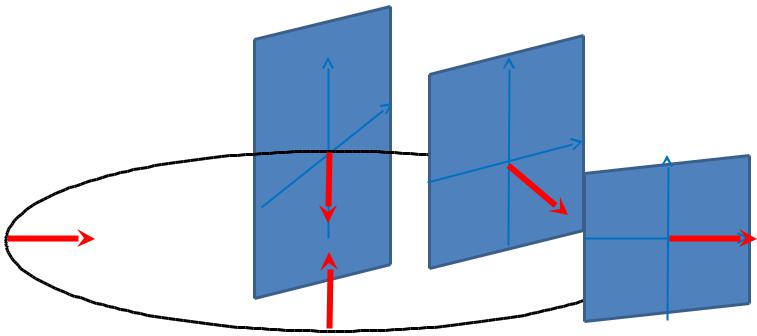
– = е–imφ |
i |
i |
|
|
1 |
1 |
i |
1
Конец стрелки описывает правую спираль вокруг траектории движения (число полных оборотов равно квантовому числу m)
| |
– |
|2 |
1 |
|
= const = —– |
||
|
|
|
2 |
(движение равномерное и строго направленное)
