Чтобы найти константу k, продифференцируем дважды любое частное решение и подставим вторую производную вместо левой части уравнения:

d²[(х)]/dx² = –k² [(х)] и –k² [(х)] = (–2mE/²) [(х)].

Отсюда получим, что k = ±(2mE)^0,5/= ± p/, где новая константа р называется квантово-механическим импульсом. Следовательно, пространственные части волновых функций стационарных состояний должны иметь вид:

(х) = А • ехр [ i (p/) x ] + В • ехр [ – i (p/) x ]

Таким образом, для каждого определенного значения наблюдаемых Е и р получаем целую совокупность стационарных состояний, описываемых суперпозиционными волновыми функциями (х). Характерная особенность полученных функций заключается в следующем: если мы будем измерять величину энергии, мы всегда получим один и тот же результат — число Е. При измерении импульса мы будем получать строго определенный результат — число | р | — только для модуля этого вектора, но знак, определяющий направление вектора импульса (и направление движения частицы) будет получаться различным, а именно: с вероятностью А² будем находить число +р и с вероятностью В² — число –р (заметим, что на возможные числовые значения энергии и модуля импульса никаких ограничений не накладывается).

Другими словами, суперпозиционные функции описывают суперпозиционные состояния, в которых направление движения частицы не определено. Среди них, однако, можно выделить два специальных состояния, для которых как модуль, так и знак вектора импульса будет строго определен:

⁺ = е ^{i kx} = е ^{i (+р/) x} ( А = 1, В = 0 )

^– = e ^{–i kx} = e ^{i (–р/) x} ( А = 0, В = 1)

Поскольку обе эти функции являются комплексными, то их конкретные значения (при заданном х) могут быть изображены вектором-стрелкой единичной длины в комплексной плоскости, которую удобно расположить перпендикулярно оси х (направлению движения частицы). При перемещении вдоль оси х эта стрелка будет поворачиваться в комплексной плоскости (вокруг оси х) с частотой, определяемой волновым вектором k = p/ . Ясно, что конец стрелки-амплитуды будет описывать спираль, закрученную по часовой стрелке или против нее, в зависимости от направления движения частицы (знака импульса).

Располагая выражениями для пространственной части волновой функции, можно проанализировать характер распределения частицы в пространстве. Для установления этого характера достаточно найти квадрат волновой функции, который показывает зависимость вероятности найти частицу в определенной точке от координаты этой точки: Р(х) = *(х) • (х) = |(х)| ²

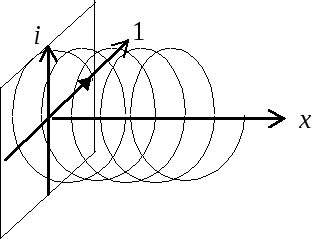
Рассмотрим такие зависимости для базисных функций ⁺ и ^–.

|⁺| ² = е ^ikx • e ^–ikx = 1 |^–| ² = е ^–ikx • e ^ikx = 1

Из полученных формул видно, что для этих двух состояний зависимость вероятности от координаты х отсутствует. Другими словами, все точки оси х полностью эквивалентны друг другу.

Необходимо отметить важную особенность полученного результата: в рассмотренных двух состояниях значения одной из наблюдаемых — импульса — строго определены, а значения другой наблюдаемой — пространственной координаты х — полностью неопределенны. Полезно построить графические изображения функций распределения для этих наблюдаемых:

из которых ясно видно, что одна из функций (Р_х) бесконечно широкая, а другая (Р_Рх) — бесконечно узкая. Такая связь между двумя наблюдаемыми является проявлением важного КМ-принципа — принципа неопределенности (Гейзенберг). Сами наблюдаемые, связанные в отношении их определенности, называются совместно неизмеримыми (несоизмеримыми, сопряженными).

Как во всяком ЛВП, в двумерном пространстве стационарных функций с определенным значением энергии можно выбрать не один базис, а бесконечно много таких базисов:

(х) = A •  ⁺ + B •  ^– = С •  ' + D •  '' = .....

Рассмотрим еще один базис, состоящий из двух следующих функций:

 ' = А (е ^ikx + e ^–ikx ) ( А = В )

 '' = А (е ^ikx – e ^–ikx ) ( А = –В )

Ввиду равенства модулей коэффициентов (А² = В²), формулы для этих двух функций могут быть преобразованы с использованием тригонометрического представления комплексных экспонент: exp ( i •  ) = cos   i • sin. Тогда получим одну чисто действительную функцию и одну чисто мнимую функцию:

 ' = 2А • cos (kx)  ' = 2 i А • sin (kx)

Графики этих функций имеют вид не спиралей, как в общем случае, а вид плоских кривых — косинусоиды, лежащей в плоскости, образованной осью х и осью действительных чисел, и синусоиды, лежащей в плоскости, образованной осью х и осью мнимых чисел:

Для функций  ⁺ и  ^– модуль всюду сохранял свое значение, равное 1, а от координаты х зависела только фаза ( = kx). В данном случае ситуация противоположная: фазы функций ' и '' сохраняются неизменными (0 и /2, соответственно), тогда как модули изменяются с координатой х по гармоническому закону. Такой характер изменения приводит к тому, что в некоторых точках оси х значение волновой функции максимально, зато в других равно 0. Точки, в которых  = 0, называются узлами (узловыми точками).

Возведение этих двух функций в квадрат приведет к получению двух функций распределения вероятностей: P'(х) = | ' | ² и P''(х) = | '' | ², которые также будут иметь вид гармонических волн, сдвинутых относительно друг друга на четверть периода:

Характерная особенность данных функций распределения — их пространственная неоднородность, доходящая до обращения вероятности в некоторых точках (в узлах) в 0. Вся ось х разбивается этими узлами на конечные ячейки длины х = /k, внутри которых частица в определенной степени локализована — вероятность для центра ячейки много больше, чем для ее краев. Можно сказать, что степень пространственной локализации в состояниях ' и '' является максимально возможной.

Другая особенность данных двух состояний обусловлена равенством А² = В², что приводит к заключению о невозможности определения направления вектора импульса частицы. При попытках измерения этой наблюдаемой будут получаться оба значения с равной вероятностью Р⁺ = А² = 1/2 и Р^– = В² = 1/2. Такой результат снова является следствием принципа неопределенности: увеличив пространственную локализацию частицы, мы уменьшили определенность сопряженной величины — проекции импульса на направление движения.

ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ

Потенциальная яма — модель системы, в которой движения частицы ограничены некоторым предельным расстоянием, на которое частица может удаляться от выделенной точки (центра). Физическая природа ограничений может быть различной. Так, например, система может быть окружена реальными жесткими стенками, от которых частица будет отражаться при столкновении. Частица может быть связана с центром жесткой или упругой связью. В любом случае, на некотором расстоянии от центра на частицу начинает действовать возвращающая сила, заставляющая частицу совершать движения циклического типа в ограниченном объеме пространства.

Ясно, что структуры, наиболее интересные для химиков — атомы и молекулы — относятся к структурам именно такого типа, так как составляющие их частицы (ядра и электроны) движутся циклическим способом в ограниченном объеме пространства. В этом случае возвращающая сила имеет электрическую природу. Поэтому с помощью простой модели потенциальной ямы можно выяснить многие важные особенности атомных и молекулярных структур.

Модель потенциальной ямы отличается от предыдущей тем, что потенциальная энергия частицы отлична от нуля, по крайней мере, в некоторых областях пространства. С физической точки зрения, это означает, что в этих областях пространства на частицу действуют внешние силы, величина которых определяется зависимостью потенциальной энергии от пространственных координат: F = – grad U(x, y, z). Поскольку характер зависимости U от x, y, z может быть весьма разнообразным, существует множество различных случаев. Среди них можно выделить некоторые стандартные ситуации:

• прямоугольная яма ("потенциальный ящик"),

• цилиндрическая яма ("жесткий плоский ротатор"),

• параболическая яма ("гармонический осциллятор"),

и некоторые другие.

ЧАСТИЦА В ПОТЕНЦИАЛЬНОМ ЯЩИКЕ

В этом случае зависимость потенциальной энергии от пространственных координат имеет следующий вид (для простоты ограничимся одномерным случаем движения вдоль оси х):

В промежутке от х = 0 до х = L потенциальная энергия нулевая, и когда частица находится здесь, на нее не действуют никакие силы. В остальных местах потенциальная энергия бесконечно велика, и поэтому частица не может выйти за пределы ящика: в момент касания стенки на частицу действует бесконечно большая сила, мгновенно обращающая направление ее движения.

Классическое описание

В классической механике такой тип движения называется возвратно-поступательным: частица все время движется равномерно и прямолинейно, но направление движения периодически изменяется на противоположное. Следовательно, классическое описание такой частицы практически ничем не отличается от описания свободной частицы, за исключением некоторой потери определенности направления движения. Все допустимые состояния частицы стационарны и каждое из них можно охарактеризовать двумя взаимосвязанными наблюдаемыми:

• энергия (Е = Т), имеющая определенное и постоянное значение, и всегда представляющей собой кинетическую энергию (за исключением точек возврата),

• импульс р и его проекция на ось х, который может иметь всего два возможных значения р_х = ± р, при этом выполняется соотношение Т = р²/2m.

В отличие от свободной частицы, для возвратно-поступательного движения можно определить еще одну наблюдаемую: частоту  = р/2mL, имеющую смысл только для достаточно длинных промежутков времени.