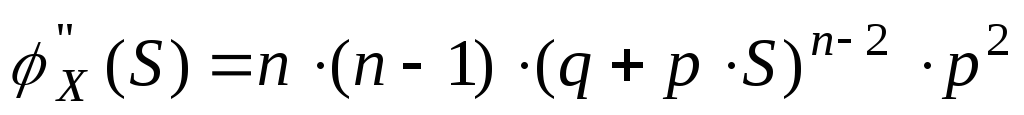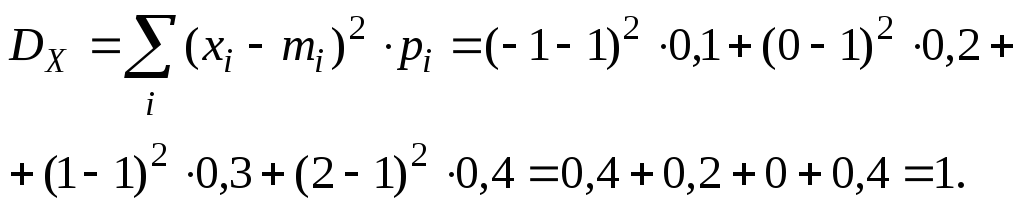Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / Шпора3
.doc|
16.Моменты n-го порядка. Дисперсия. Среднее квадратическое отклонение. МО в теории вероятностей относится к типу характеристик положения (см. далее мода, медиана), кроме них используется еще ряд числовых характеристик различного назначения, среди них особое значение имеют моменты (начальные, центральные). Положим
Опр.
Начальным
моментом S-го
порядка СВ Х
называется
Замечание. Иногда
используются абсолютные начальные
моменты S-го
порядка
Для
СВДТ:
Для
СВНТ:
Замечание.
Обозначим
Определение.
Центральным моментом S-го
порядка называется
Замечание. Иногда используются абсолютные центральные моменты S-го порядка.
Для СВДТ:
Для СВНТ:
Определение.
Центральный момент II-го
порядка ( Для СВДТ:
Для СВНТ:
Опр. Свойства дисперсии: 1.
Доказательство:
2.
Доказательство:
По свойству 4 МО и с учетом неравенства (*) получаем доказательство свойства 2 для дисперсии.
3.
Доказательство:
20.Распределение Пуассона. Опр.
СВДТ Х
имеет распределение Пуассона, если
ее возможные значения 0, 1, 2, …, m,
… (счетное множество значений), а
соответствующие вероятности выражаются
формулой
Замечание. Закон Пуассона зависит только от a, смысл этого параметра состоит в следующем, он одновременно является МО и дисперсией СВ Х.
Рассмотрим условия, при которых возникает Пуассоновское распределение. Покажем, что оно является предельным, для биноминального распределения при n и одновременно р0, но nра (а~0,1–10). Теорема (Пуассона). Если n, р0, но npа, то фиксированного значения m, где m=0,1,…
Доказательство.
фиксированного значения m.
Комментарии: Так как n-велико, а вероятность p - очень мала, то в каждом отдельном опыте “успех” приходит редко. Поэтому закон Пуассона в литературе называется законом редких явлений. Пример. Завод отправил на базу n=5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится p=0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. n=5000. p=0,0002.
Имеются
специальные таблицы, с помощью которых
можно найти
|
17.Мода, медиана и квантили МО не единственная характеристика положения, применяемая в теории вероятностей. Опр.
Модой
СВДТ Х
называется такое возможное значение
Модой
СВНТ Х
называется действительное число
Пример.
Замечание. Мода может не существовать, иметь единственное значение, такие распределения называются унимодальное, или иметь множества значений – полимодальное распределение. Наличие более чем одной моды, часто указывает на разнородность статистического материала, который положен в основу исследований.
Опр.
Медианой
СВ Х
называется действительное число
Эта
характеристика применяется, как
правило, только для СВНТ и геометрически
медиана, это абсцисса той точки на
оси ОХ, для которой площади под графиком
Замечание. В случае симметричного распределения (имеющего моду) три характеристики: 1) МО ; 2) мода; 3) медиана совпадают. Замечание.
Уравнение
Опр.
Квантильлью
порядка р распределения
СВНТ Х
называется действительное число
Замечание.
Медиана
18.Целочисленные СВ и их производящие функции В ряде случаев при определении важнейших числовых характеристик дискретных СВ может помочь аппарат производящих функций. Опр. Дискретную СВ Х, принимающую только целые, неотрицательные значения называют целочисленной СВ.
Закон
распределения целочисленной СВ
определяется
Закон распределения целочисленной СВ удобно изучать с помощью производящей функции, которая определяется, как
В
соответствии с определением МО:
Этот
ряд сходится абсолютно при
Поскольку
Замечание
В математике рассматриваются произвольные производящие функции.
Замечание
Возьмем первую производную по S от производящей функции.
Возьмем вторую производную по S от производящей функции
То есть можно выразить начальные моменты более высокого порядка, через начальные моменты более низкого порядка.
|
19.Биномиальное распределение Опр.СВДТ Х имеет биномиальное распределение, если ее возможные значения 0, 1, 2, …, m, …, n, а соответствующие вероятности
Это распределение зависит от двух параметров: n, p.
В
литературе
Рассмотрим условия, при которых возникает биномиальное распределение. Пусть производится n независимых опытов (испытаний), в каждом из которых событие А (“успех”) появляется с вероятностью p, СВ Х – это число успехов при n-опытах. Коментарии: Опыты называются независимыми, если вероятность какого-либо исхода каждого из них не зависит от того, какие исходы имели другие опыты. Покажем, что СВ Х имеет биномиальное распределение.
Если успех ставим в соответствие 1. Если неуспех ставим в соответствие 0.
m штук – “1” n–m штук – “0”.
Так
как опыты независимы, то каждый такой
вариант имеет вероятность
Найдем
важнейшие числовые характеристики
Воспользуемся производящей функцией
Возьмем производную по S.
Пример. Передается 5 сообщений по каналу связи (n = 5). Каждое сообщение с вероятностью p = 0,3, независимо от других искажается. СВ Х – количество искаженных сообщений. Построить ряд распределения, МО, DX, X, моду, а также вероятность того, что будет искажено не менее двух сообщений.
продолжение таблицы:
прожолжение16: Пример.
1) Способ.
2) Способ.
Дисперсия СВ Х является характеристикой рассеивания, то есть она характеризует разбросанность СВ Х около ее МО. Дисперсия имеет размерность квадрата СВ, что не всегда удобно, поэтому очень часто используется среднее квадратическое отклонение, которое имеет размерность самой СВ. Механическая интерпретация МО и дисперсии.
Пусть на прямой
в точках
– момент инерции
масс
Таким образом,
МО характеризует место, вокруг которого
группируются массы
Пример.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||

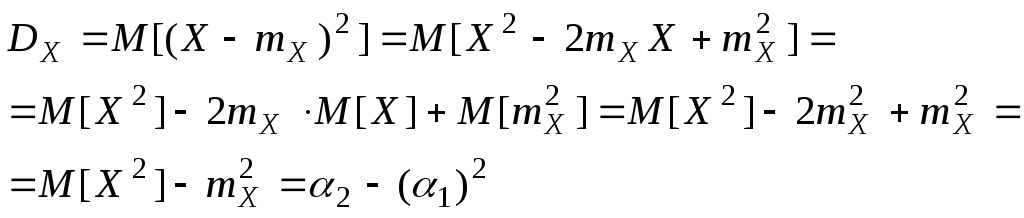 .
.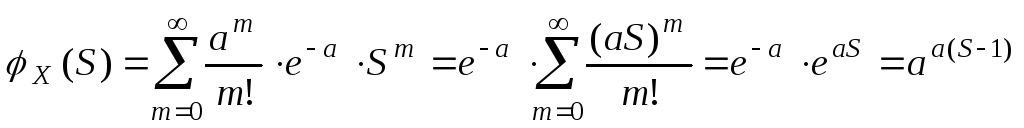




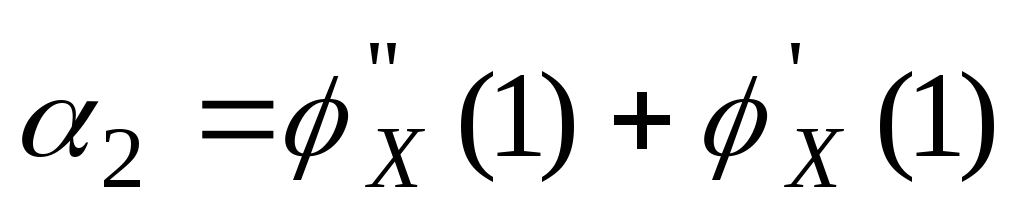 .
.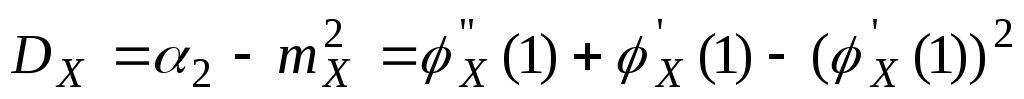 .
. .
.