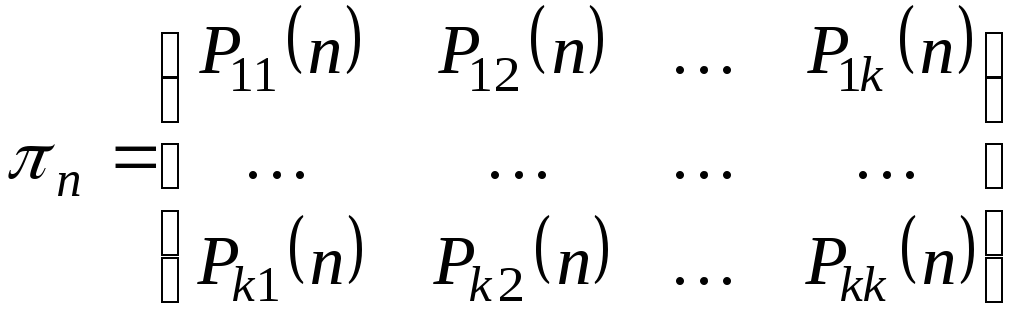Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / Шпора14
.doc|
57.
Критерий
Критерий
Процедура
применения критерия
Этапы:
Если
Х–СВНТ – разбить множество значений
на r
– непересекающихся интервалов
Х–СВНТ
вычислить
e – количество оцениваемых параметров. Малочисленные частоты надо будет объединять. Проверка гипотезы о равномерном распределении генеральной совокупности. n = 200 А;
1.
2.
k = 10 – 2 – 1 = 7
|
59. Переходные вероятности.
Матрица
перехода.
Далее будем рассматривать только
однородные цепи Маркова, в которых
условная вероятность появления
события
Назовем
эту вероятность – вероятностью
перехода и обозначим
Полную вероятностную картину возможных изменений, осуществляющихся при переходе от одного испытания к следующему можно задать с помощью матрицы
Замечание.
Опр. Любая квадратная матрица, элементы которой удовлетворяют следующим требованиям:
Одной из главных
задач в теории цепей Маркова является
задача определения вероятности
перехода
Рассмотрим
какое-нибудь промежуточное испытание
с номером (S+m).
В этом испытании осуществится
какое-либо одно из возможных событий
По формуле полной вероятности получим
Обозначим через
Согласно формуле
(*) получаем, что
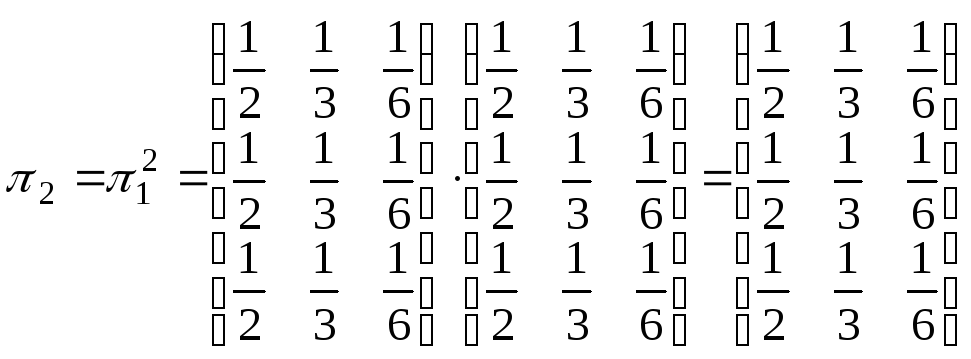
В частности, когда n = 2, получаем
n = 3
Отметим частный случай формулы (*), когда m = 1
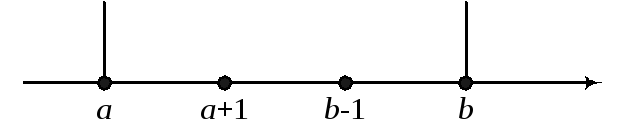
Пример 2 Процесс блуждания с отражением. Процесс блуждания с отражением.
Пусть частица,
находящаяся на прямой, движется по
этой прямой под влиянием случайных
толчков, происходящих в моменты
времени
Получается цепь Маркова с конечным числом состояний.
Аналогично можно рассматривать ситуации, когда частица прилипает к одной из стенок, этот процесс блуждания с поглощением. Лекция № 23 Пример 3. Вероятности перехода даются матрицей
Чему равно число состояний в системе? Ответ: 3. Найти вероятности перехода из состояния в состояние за два шага:
|
58. Марковская зависимость испытаний. Определение цепи Маркова.Непосредственным обобщением схемы независимых испытаний является схема цепей Маркова. Пусть производится последовательность испытаний, в каждом из которых может осуществляться одно и только одно из k несовместных событий.
верхние индексы обозначают номер испытания.
Опр.
Последовательность
испытаний образует простую цепь
Маркова, если условная вероятность
в
Замечание.
Часто при изложении теории цепей
Маркова придерживаются иной терминологии
и говорят о некоторой физической
системе S,
которая в каждый момент времени может
находиться в одном из состояний
Для
цепей Маркова вероятность перейти в
какое-либо состояние
Пример
1. В модели
Бора атома водорода, электрон может
находиться на одной из допустимых
орбит. Обозначим, через
Разность (i–j) зависит от количества энергии, на которую изменился заряд атома в момент времени tS. Это пример цепи Маркова с бесконечным числом состояний.
|

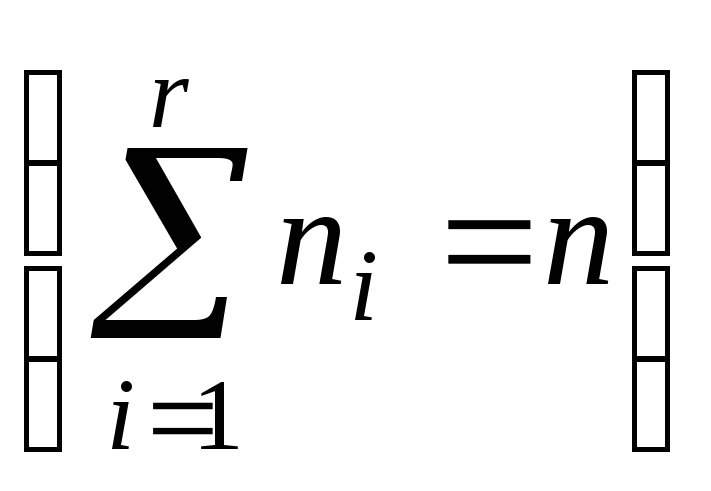 .
.

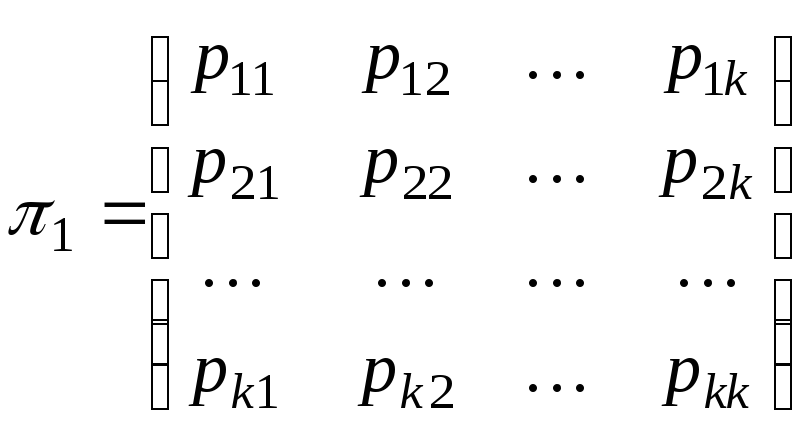 – матрица
перехода
– матрица
перехода