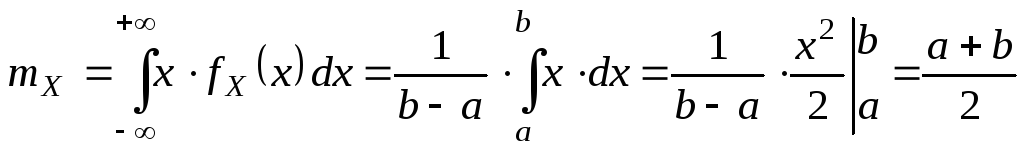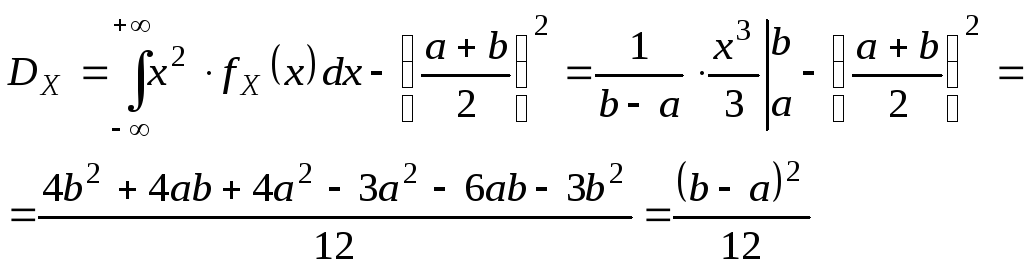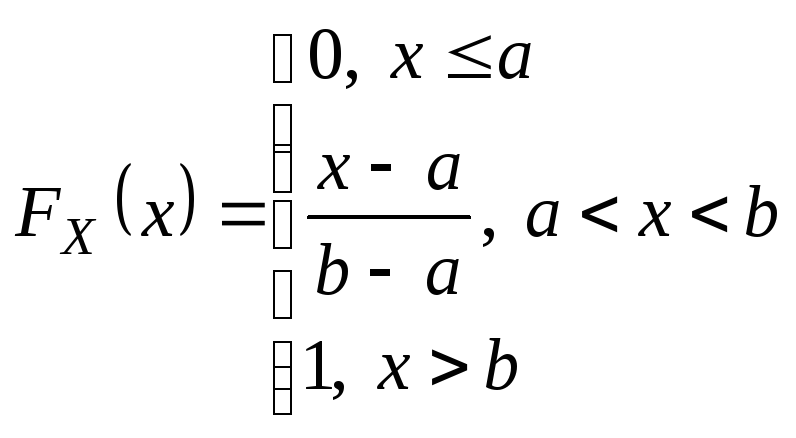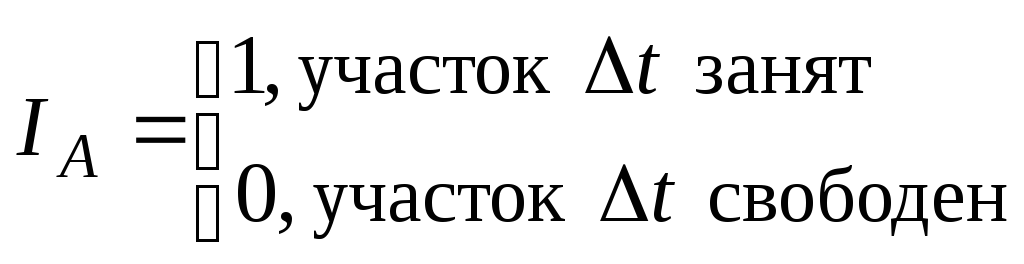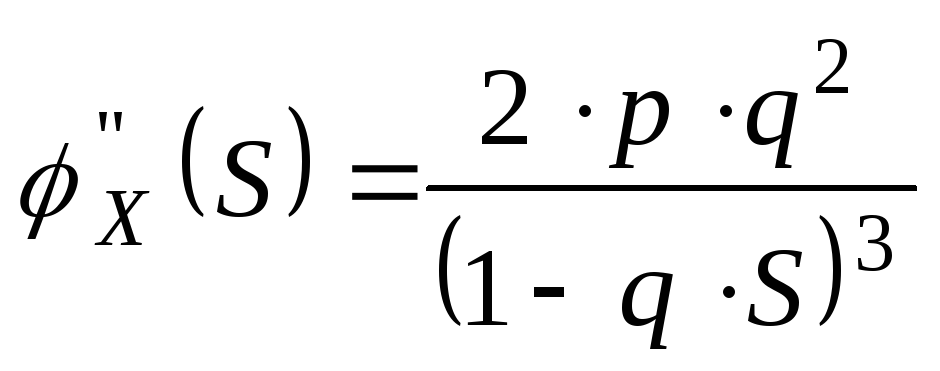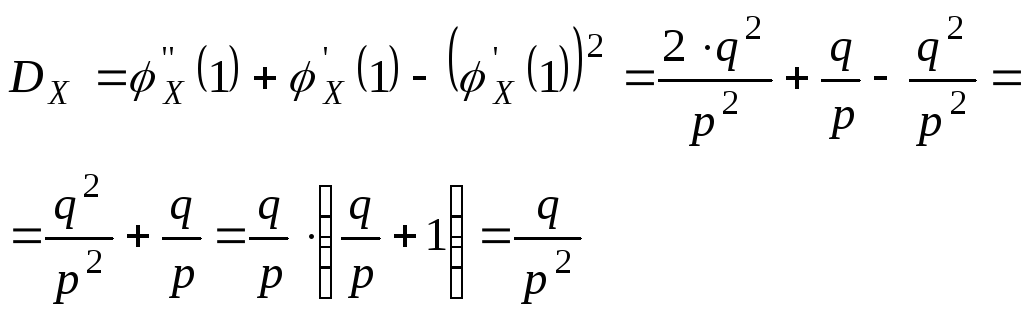Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / Шпора4

22.Локальная предельная теорема Муавра-Лапласа.

Биномиальное распределение имеет МО равное np .

Пусть p – не близко к 0 и 1.

Теорема.

Если в схеме независимых испытаний , то для любого равномерно по всем вида , где m – неотрицательные целые числа

Замечание.

Эти таблицы даются, только для .

Пример.

Вероятность изделию некоторого производства оказаться бракованным равна 0,005 (p = 0,005). Чему равна вероятность того, что из n = 10000 наудачу взятых изделий, бракованных изделий окажется равно .

Решение

1) .

2)

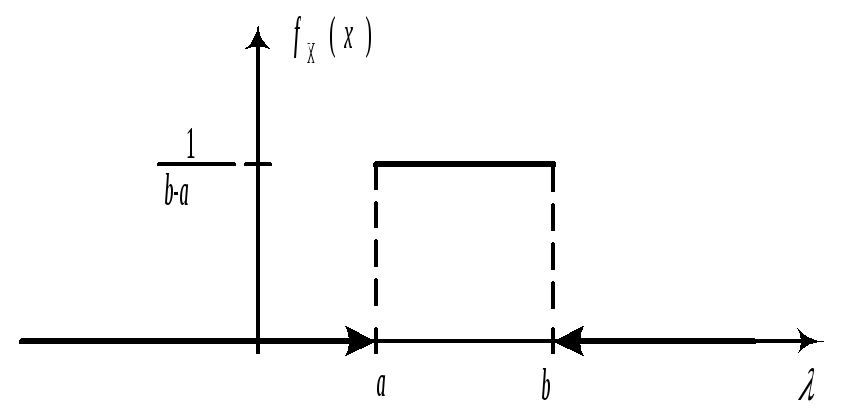
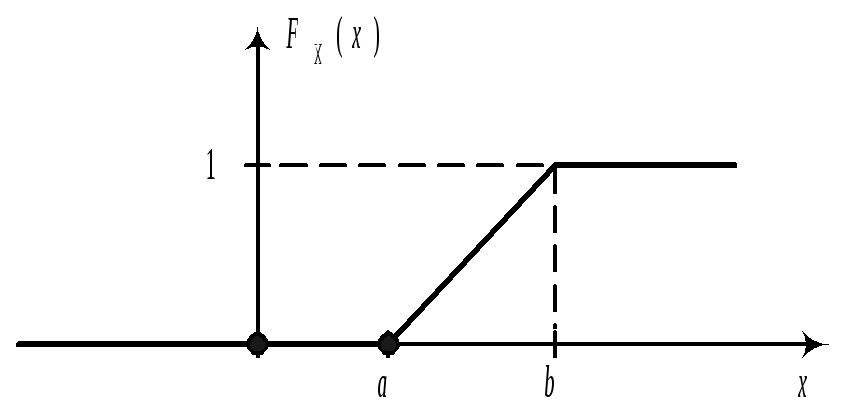
25. Равномерное распределение

Опр.СВНТ Х называется распределенной равномерно на , если , .

Найдем константу С.

;

;

.

Пример.

Шкала измерительного прибора проградуированных в некоторых единицах. СВ Х – ошибка при округлении отсчета до ближайшего целого деления, то она будет иметь равномерное распределение на . Найдем – ?

Решение.

Замечание.

Моды равномерное распределение не имеет, а медиана совпадает с МО.

.

Найдем функцию распределения и построим ее график.

I Случай

.

II Случай

.

III Случай

.

21. Простейший Пуассоновский поток

На практике часто встречаются ситуации, где имеет место распределение Пуассона.

Задача.

Пусть на оси времени 0t случайным образом возникают точки моменты появления каких-то однородных событий. (Например, вызовы на телефонной станции, приход посетителей в магазин и т.д.)). Последовательность таких моментов назовем потоком событий.

Предположим, что поток обладает следующими свойствами.

Свойства.

1. Стационарность.

Это свойство означает, что вероятность попадания, того или иного числа событий, на участок времени длиной  не зависит от того, где на оси 0t расположен этот участок, а зависит только от его длины .

Из этого следует, что среднее число событий, появляющееся в единицу () времени , постоянно.

 – интенсивность потока.

2. Ординарность.

Это свойство заключается в том, что вероятность попадания на малый участок t двух или более событий пренебрежимо мала с вероятностью попадания на него одного события.

Т.е. при t0 вероятность двух или более событий является бесконечно малой более высокого порядка малости, чем вероятность попадания на него одного события.

3. Отсутствие последствия.

Это свойство означает, что вероятность попадания некоторого числа событий на заданный участок оси 0t не зависит от того сколько событий попало на любой другой не пересекающийся с ним участок (в частности “будущее” потока не зависит от его “прошлого”).

Опр. Поток событий, обладающий этими 3-мя свойствами называется простейшим (или стационарным) Пуассоновским потоком.

Покажем, как простейший Пуассоновский поток связан с распределением Пуассона.

СВ Х – количество событий, попадающих на участок 0t, длиной .

Покажем, что Х имеет распределение Пуассона.

Доказательство:

Разделим участок длины  на n равных частей .

МО числа событий, попадающих на элементарный участок t, равно . Согласно свойству 2 (ординарности) можно пренебречь вероятностью попадания на элементарный участок t, двух или более событий.

Назовем элементарный участок t – занятым, если на нем появилось событие из потока.

Назовем элементарный участок t – свободным, если на нем не появилось событие из потока.

A = {участок t занят}

– вероятность того, что участок t занят.

Среднее число, то есть МО числа событий, попадающих на участок длины t, будет равно .

.

Рассмотрим теперь n-участков на временной оси, как n-независимых испытаний (опытов), в каждом из которых (независимость этих испытаний  из свойства 3) может появиться событие А и вероятность этого события . Число занятых элементарных участков – это и есть Х.

СВ Х имеет биномиальное распределение

.

Будем теперь неограниченно увеличивать число элементарных участков и найдем при .

Согласно теореме Пуассона, при ,

Пример.

На АТС поступает простейший поток вызовов с интенсивностью =0,8 (вызовов/мин). Найти вероятность того, что за 2 минуты:

а) не придет ни одного вызова;

б) 1 вызов;

в) хотя бы 1 вызов.

Решение.

Х – количество вызовов за 2 минуты.

а) .

б) .

в) .

24.Геометрическое распределение

Опр.СВДТ Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, …, m, …, а вероятности этих значений

Комментарий

Вероятности для последовательных значений m образуют геометрическую прогрессию с первым членом p и знаменателем q.

На практике геометрическое распределение появляется в следующих условиях. Пусть производится ряд независимых испытаний (опытов) с целью получения какого-то результата (“успеха”) А. При каждом опыте “успех” достигается с вероятностью p.

СВ Х – это число безуспешных опытов до первой попытки, в которой появляется результат А.

Ряд распределения имеет следующий вид.

Найдем числовые характеристики СВ Х распределенной по геометрическому закону.

На практике чаще приходится рассматривать не СВ Х, имеющую геометрическое распределение, а .

– это число попыток до первого успеха, включая удавшуюся.

Ряд распределения

– геометрическое распределение, сдвинутое на 1 (геометрическое плюс 1).

Пример.

Стрелку выдаются патроны до тех пор, пока он не промахивается.

Вероятность попадания при каждом выстреле

. Какова вероятность того, что он получит не менее трех патронов.

Решение.

Пусть Х – это количество патронов, которое получит стрелок.

23 Интегральная предельная теорема Муавра-Лапласа

Теорема.

При равномерно по

Замечание.

– затабулирована.

Ее значения приводятся только для .

Пример.

Вероятность изделию некоторого производства оказаться бракованным равна 0,005 (p = 0,005).Чему равна вероятность, что из n = 10000 наудачу взятых изделий, бракованных окажется не более 70 (m = 70).

– ?
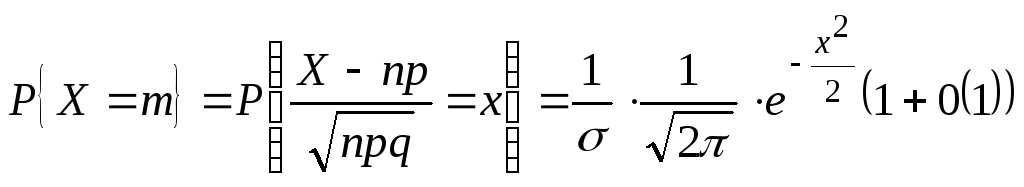
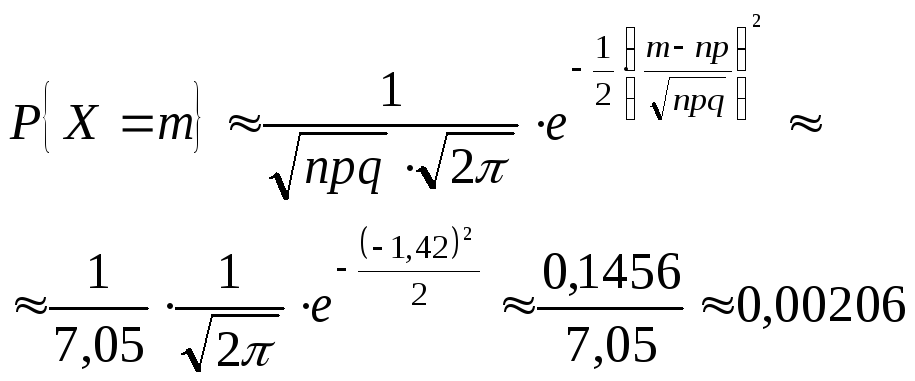
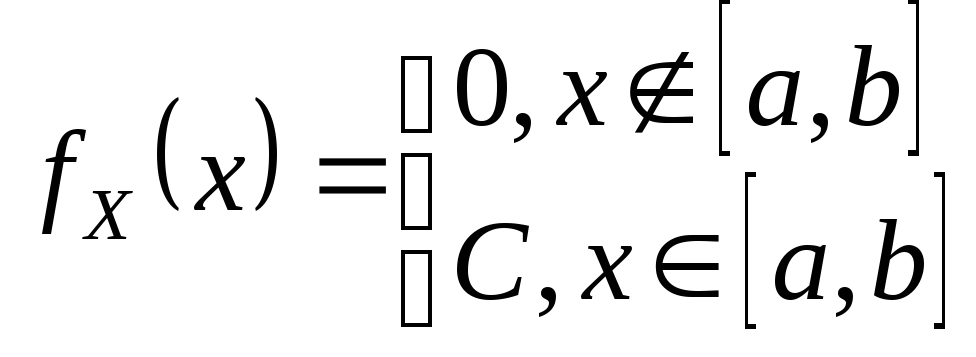