Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / Шпора2

12. Случайные величины и законы их распределения

Пусть (Ω, A, P) – произвольное вероятностное пространство. Определение. Числовая функция от элементарного события называется случайной величиной (СВ), если

 A (*)

Комментарий. Смысл определения состоит в следующем: поскольку не любое подмножество пространства Ω является событием, и все события составляют -алгебру подмножества A, то, естественно, рассматриваются только такие функции , для которых имеет смысл говорить о вероятности попадания в достаточно большие числовые множества. Свойство (*) гарантирует, что для любого X неравенство есть событие, а, значит, имеет смысл говорить о его вероятности.

Замечание. Если вероятностное пространство (Ω,A,P) является конечным, то случайной величиной называется любая числовая функция от элементарного события.

Определение. Множество возможных значений случайных величин X называется область значений числовой функции . Если это множество является конечным или счетным, то случайная величина называется случайной величиной дискретного типа (СВДТ). Если это множество является несчетным, то случайная величина называется случайной величиной непрерывного типа (СВНТ).

Пример 1. СВДТ. Опыт – бросание игральной кости. СВ X – число выпавших очков. Множество значений – {1, 2, 3, 4, 5, 6}.

Пример 2. СВНТ. Опыт – дважды измеряется емкость конденсатора, с помощью точных приборов. СВ X – разность между результатами первого и второго измерений.

Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.

Если случайная величина X имеет данный закон распределения, то мы будем говорить, что она распределена по этому закону (подчинена этому закону распределения).

Наиболее простую форму можно придать закону распределения СВДТ, обычно этот закон задается рядом распределений.

Рядом распределений СВДТ Х называется таблица

,

Так как

– попарно несовместны, и сумма этих событий образует .

.

С помощью этой таблицы можно найти вероятности любых событий.

Пример

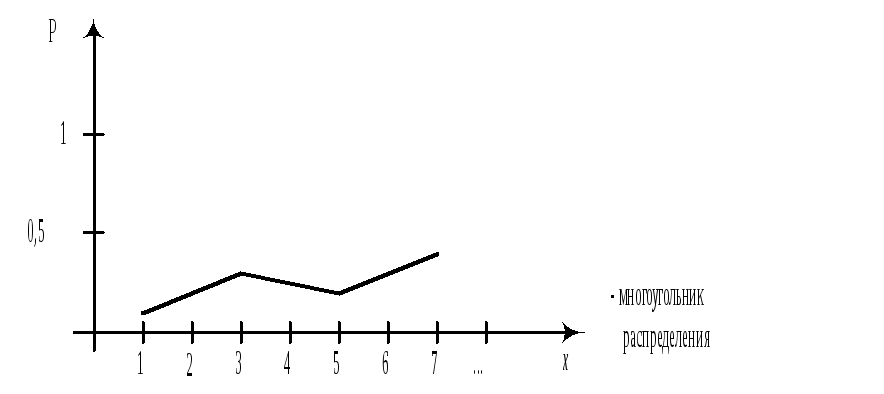
Часто бывает удобно иметь графическое изображение ряда распределения, так называемый многоугольник ряда распределения.

Часто удобной бывает механическая интерпретация СВДТ.

Аналитическое задание СВДТ

Примеры1. Гипергеометрическое распределение.Это распределение числа белых шаров (X) в выборке без возвращения, объем выборки n, из урны, содержащей М – белых шаров и (N–M) – черных шаров.

2. Равномерное распределение на множестве

3.

3)

13.Функция распределения случайной величины. Её свойства. Функция распределения СВДТ.

Ряд распределения может быть построен только для СВДТ, для недискретных случайных величин из-за несчетности множества возможных значений такое представление невозможно. Наиболее общей формой закона распределения пригодной для всех типов случайных величин является функция распределения.

Функция называется функцией распределения СВ Х .

С помощью функции распределения можно выразить вероятности попадания CB Х в различные интервалы вида

Пусть , тогда разложим в сумму двух несовместных событий

тогда

(**)

Событие можно представить, как счетную сумму несовместных событий

Согласно (**).

Теорема.

Функция обладает следующими свойствами:

1. – не убывает;

2. – непрерывна слева;

3. ;

4. .

Доказательство:

1.Следует из (**), т.к. .

2.Следует из аксиомы непрерывности 4, т.к. события

.

Свойства 3, 4 вытекают из аксиомы счетной аддитивности (3*), т.к. , где , тогда

Пусть

(по теореме Вейeрштрасса).

.

Лекция 6.

Из равенства следует, что в точках разрыва функции имеет место положительная вероятность.

Так как при каждом натуральном n может быть не более n-точек x с вероятностями , то у функции имеется не более счетного числа точек разрыва.

Обозначим через все точки разрыва функции , если вероятности таковы, что , то это равносильно тому, что СВ X имеет дискретное распределение, то есть является СВДТ.

Замечание.

Для СВДТ имеет ступенчатый вид.

Пример.

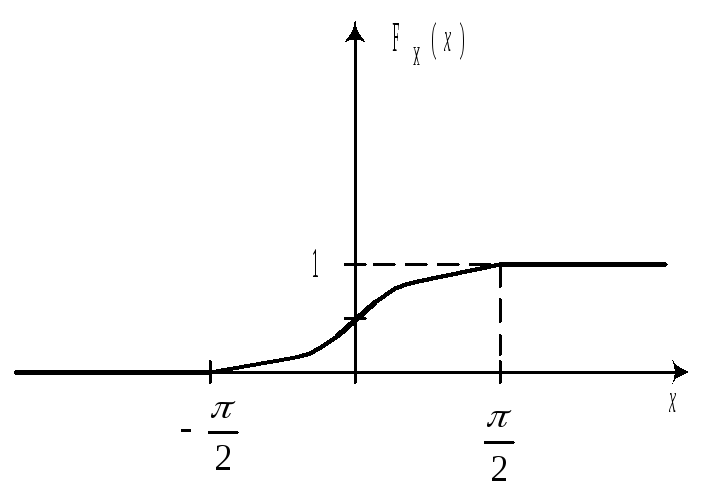
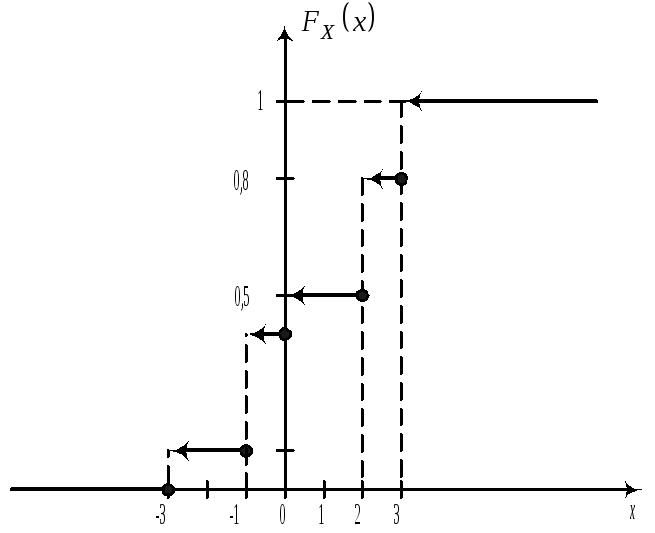
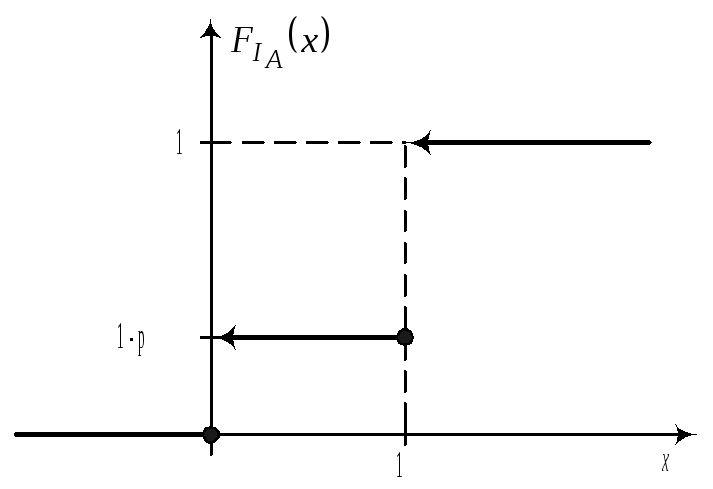
Получить функцию распределения и построить ее график.

Решение.

Введем новое важное понятие индикатора события.

Опр. Индикатором события A  A называется СВ : .

Ряд распределения случайной величины имеет следующий вид

где р-вероятность события А.

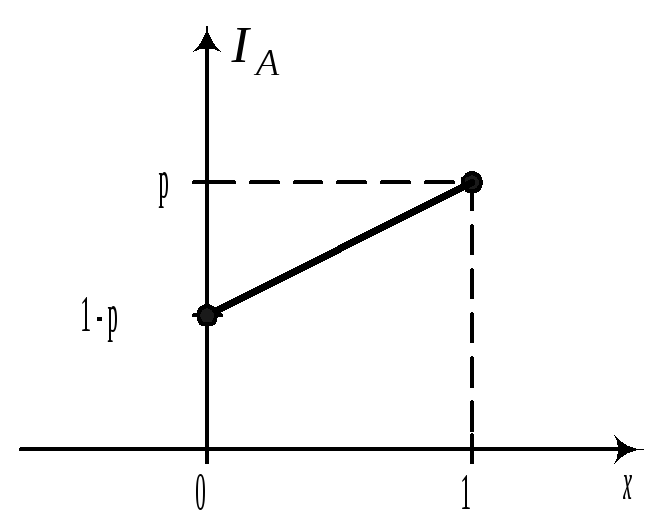
Многоугольник распределения

Функция распределения

14. Непрерывная СВ. Плотность распределения.

Опр. Функция есть плотность распределения СВ X, если

(***)

Из определения (***) следуют свойства плотности распределения.

Свойства

1.

Замечание.

Для СВ X имеющей функции. Плотности из свойства 1 и теоремы из курса математического анализа (о непрерывности интеграла с переменным верхним пределом)  что непрерывна.

2. в точках непрерывности .

3. .

4. , т.к. неубывающая функция, то .

5. Условия нормировки: .

Опр. СВ X называется СВНТ, если ее распределение имеет функцию плотности .

Через плотность можно выразить любую вероятность

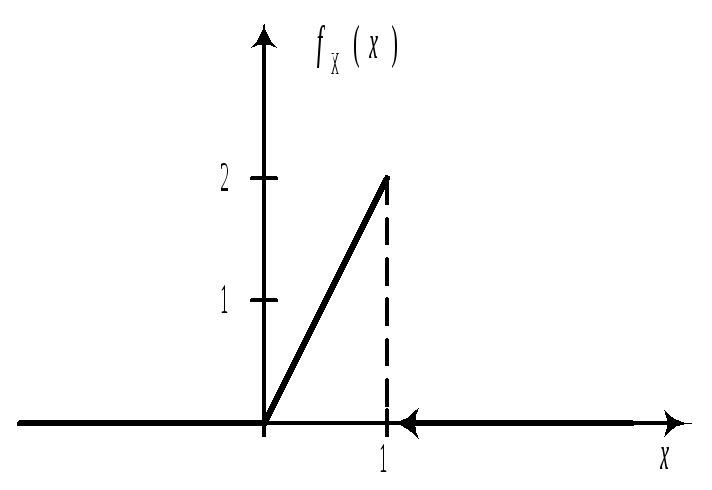
Примеры.

I.

1. a – ?

2. и построить ее график – ?

3. 

Решение.

1)Так как непрерывная в точке 1 и , то .

2)

3)

II.

1. a – ?

2. и построить ее график – ?

3. 

1).

2)

1.

2.

15. Математическое ожидание

Пусть вероятность P на конечном вероятностном пространстве (, A , P) определяется с помощью элементарных вероятностей .

Опр. МО случайной величины называется сумма

Замечание. В литературе математическое ожидание часто называют средним значением X.

Из определения МО –­ вытекают следующие свойства

Свойства:

1. .

Доказательство:

2. Аддитивность: .

Доказательство:

Замечание.

Из свойства 2 по индукции выводится свойство конечной аддитивности.

3. .

Доказательство:

4. Если , то .

Доказательство:

По свойствам 2 и 3

.

5. МО СВ X выражается через ряд распределения СВ X с помощью формулы

Доказательство:

Так как СВ , тогда .

Пусть – некоторая числовая функция, подставляя вместо аргумента x СВ Х, получим новую СВ

– ?

1 способ. С помощью закона распределения Y;

2 способ. С помощью формулы

.

Докажем формулу для .

.

Все дальнейшие выкладки повторяют свойство 5.

Пример.

а) – ?

б) Найти двумя способами, где Y= X².

Решение

.

Y	0	1	4
P	0,2	0,4	0,4

1способ:.

2 способ: .
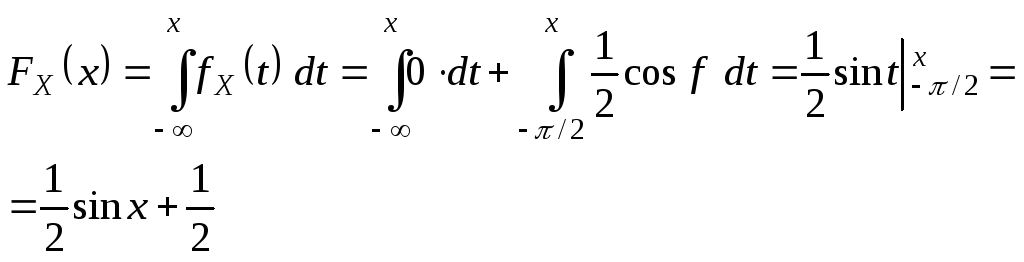
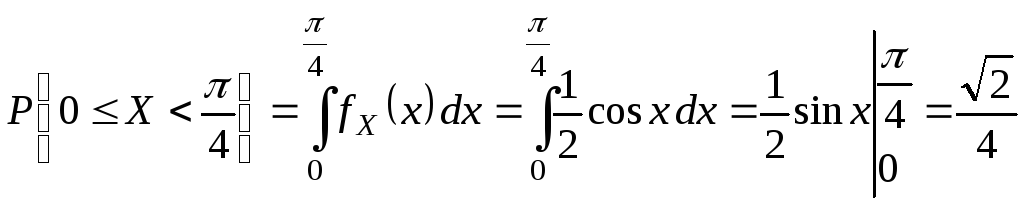
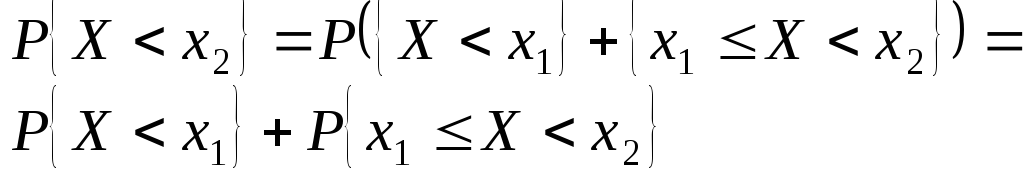
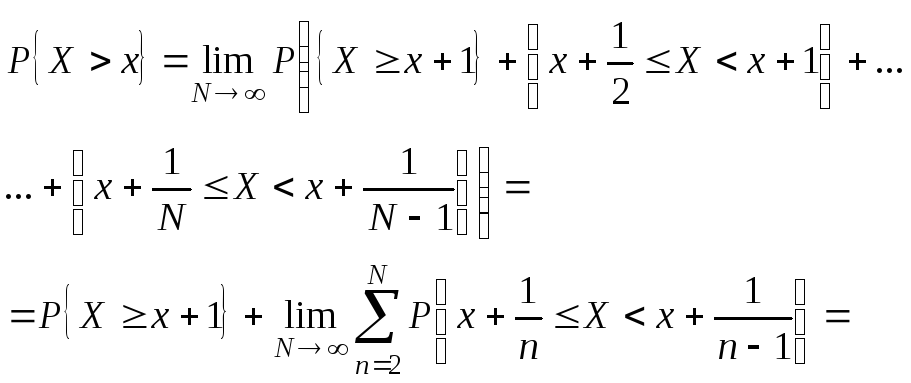
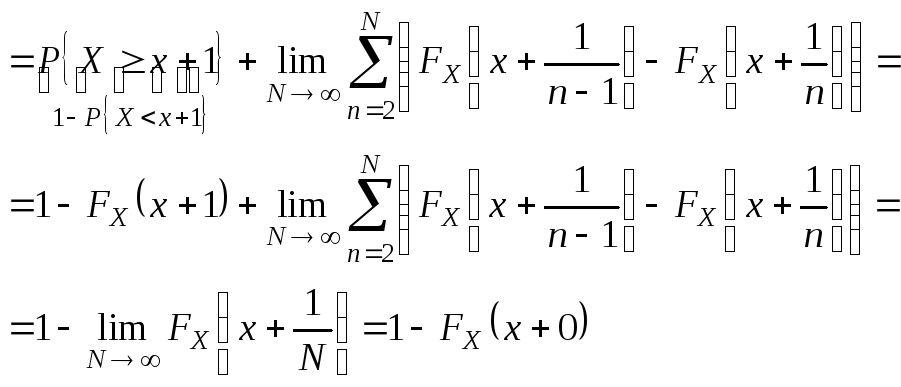
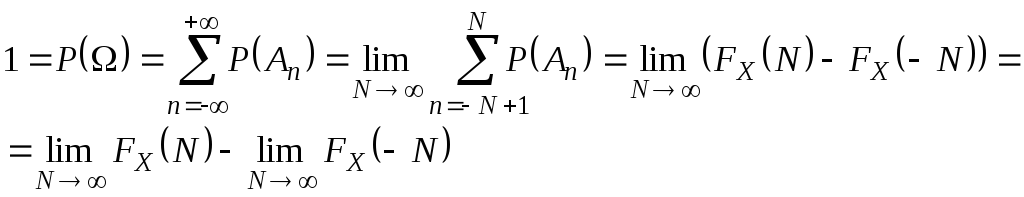
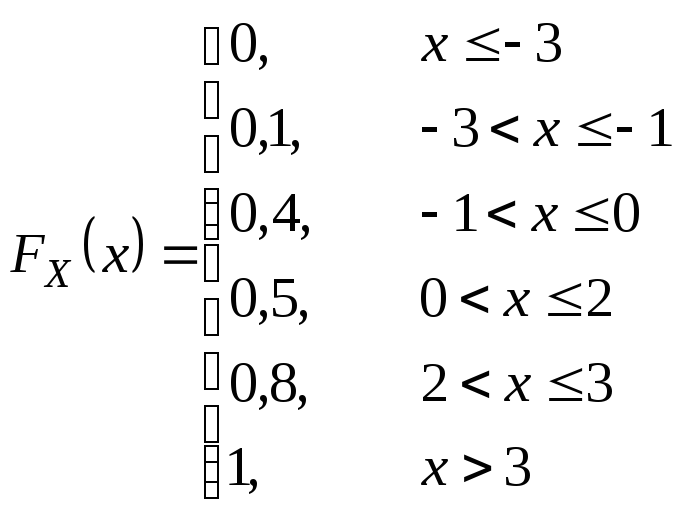
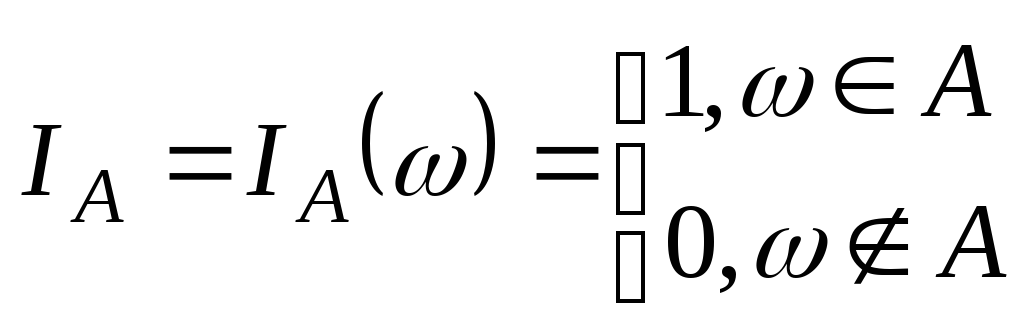
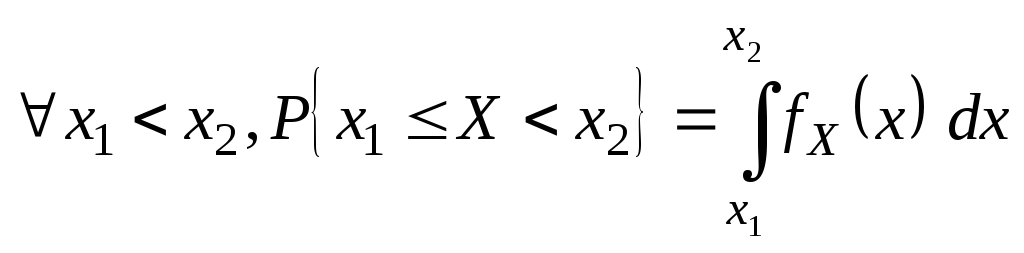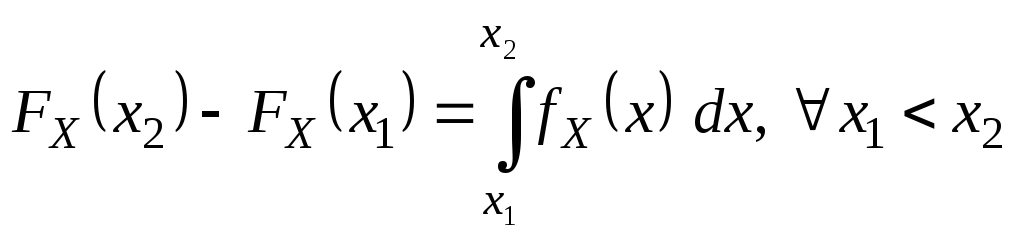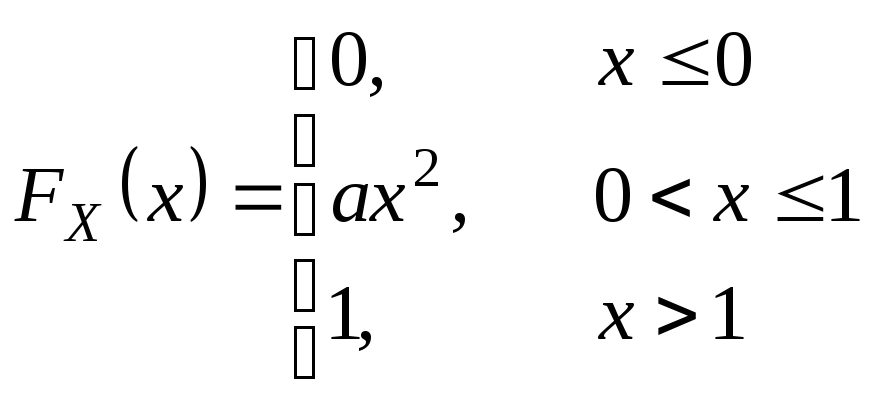
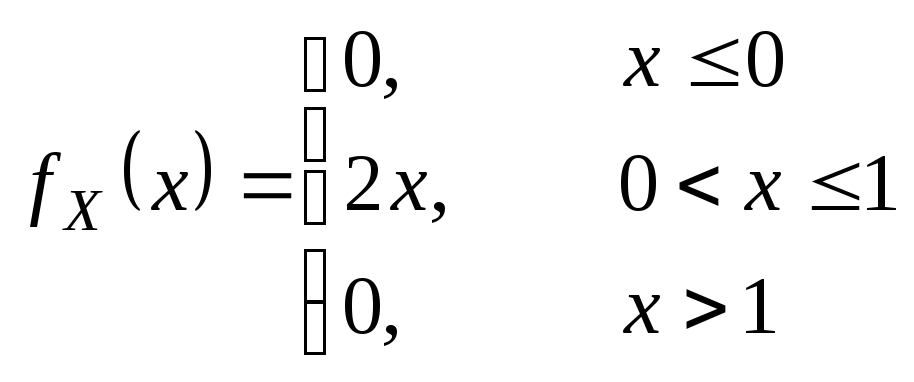
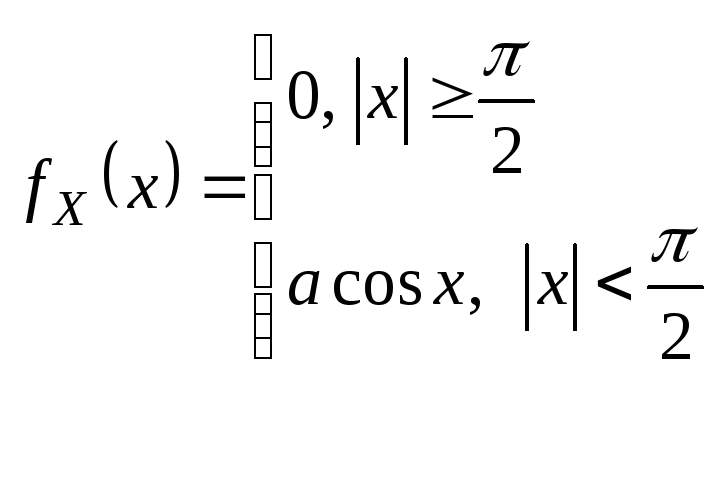
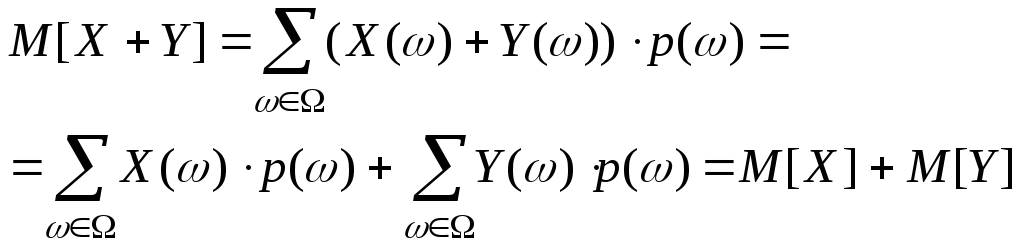
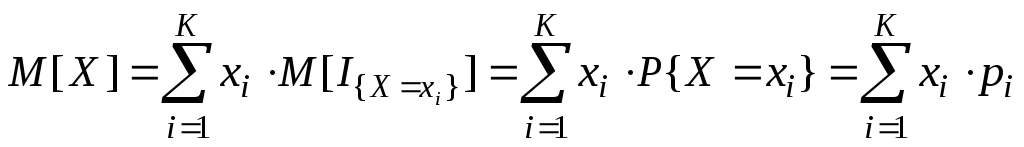