КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 3

§ 6. Геометрические вероятности

Геометрические вероятности – класс моделей вероятностных пространств, дающий геометрические вероятности.

Пусть Ω={ω} – ограниченное множество n-мерного евклидова пространства с конечным n-мерным объёмом.

Событиями назовём подмножества Ω, для которых можно определить n-мерный объём.

Для любого A  A положим

, где |V|-n-мерный объем множества V  A.

Это вероятностное пространство служит моделью задач, в которых частица случайно бросается в область Ω. Предполагается, что положение частицы равномерно распределено на множестве Ω, т. е. вероятность попадания частицы в подмножество A пропорциональна n-мерному объёму этой области.

Замечание.

В классе конечных вероятностных пространств в систему A входили все подмножества Ω. При геометрическом определении вероятности в качестве A уже нельзя взять все подмножества Ω, так как некоторые из них не имеют n-мерного объёма.

Примеры

1. Стержень разламывается на две части в случайной точке, равномерно распределённой по длине стержня. Найти вероятность того, что длина меньшего обломка окажется не больше трети длины всего стержня.

Обозначим за x расстояние от фиксированного конца стержня до точки излома.

, .

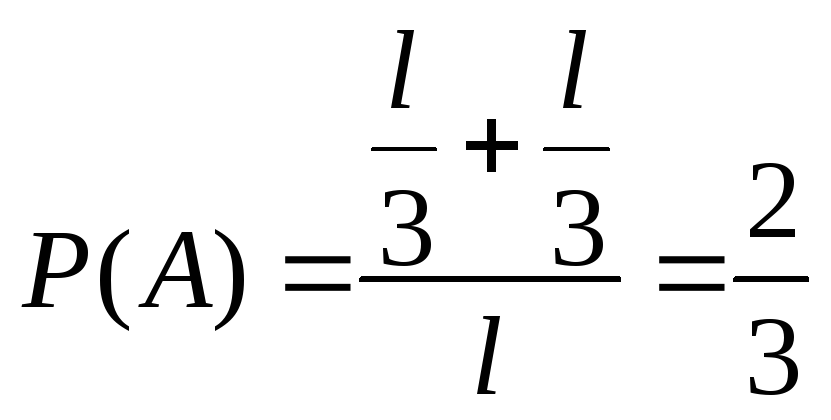2. Задача Бюффона.

Плоскость расчерчена па-раллельными прямыми, расстоя-ние между которыми равно a. На плоскость наудачу брошена игла длины l (l<a). Найти вероятность того, что игла пересечет какую-либо прямую.

Решение.

Пусть y – расстояние от центра иглы до ближайшей прямой , а x – ост-рый угол, составленный иглой с этой прямой . Пара чисел (x, y) задаёт положение иглы с точностью до выбора конкретной прямой.

– игла пересекает прямую.

.

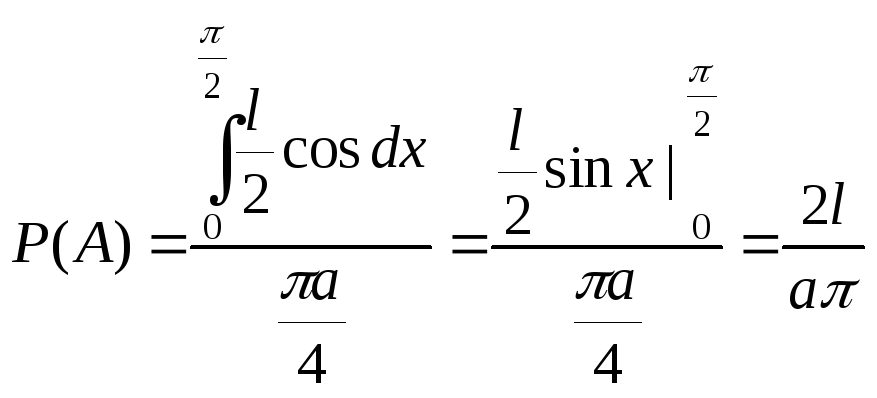Глава 2. Условные вероятности; независимость

§ 1. Условные вероятности; теорема умножения

N – число испытаний;

A, B, AB – события;

N(A), N(B), N(AB) – частоты событий;

– условная относительная частота события A при условии, что произошло событие B;

; ;

.

Если все относительные частоты событий устойчивы, тогда условная относительная частота тоже устойчива.

Пусть P(B)>0.

Условной вероятностью P(A|B) события A при условии, что событие B произошло, называется отношение .

P(A|B) = P_B(A) (встречается в литературе).

Теорема умножения

Если P(A)>0, P(B)>0, а P(A|B), то вероятность произведения .

Доказательство:

Доказательство следует из определения.

Пример

1 способ. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность того, что оба шара будут белыми.

A = {1 вынутый шар белый}

B = {2 вынутый шар белый}

AB = {оба шара белых}

,

.

2 способ. .

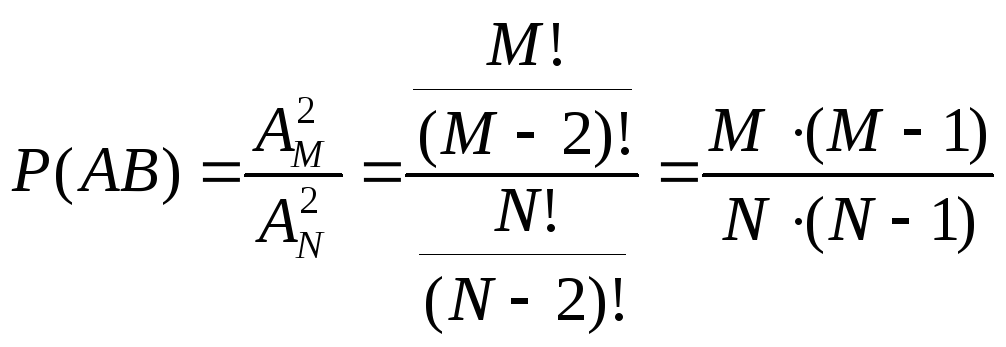Следствие.

Пусть события таковы, что тогда

.

Доказательство:

Доказательство проводится методом математической индукции.

§ 2. Формула полной вероятности

Система событий называется конечным разбиением (разбиением) пространства , если они:

1. попарно несовместны, т.е. , если i  j.

2. .

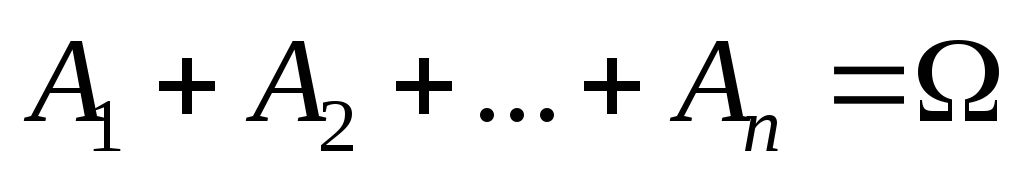Теорема (Формула полной вероятности)

Если – разбиение и все , то для всех событий B .

Доказательство:

Пример.

В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность события B={второй вынутый шар белый}.

A = {первый шар белый}

= {первый шар черный}

Решение

A = 

A + = 

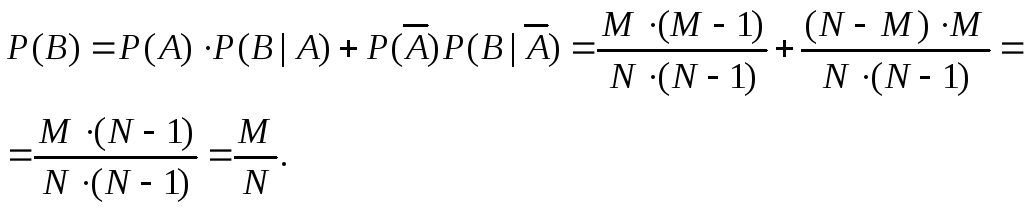
Пример показывает, что при правильно организованной жеребьевке шансы будут равны.