Лекция 15.

Глава 5. Законы больших чисел и предельные теоремы теории вероятности.

§5.1. Законы больших чисел.

Все законы делятся на две группы:

1. о вероятностях больших выбросов (больших отклонениях от математического ожидания);

2. о сходимости случайных последовательностей.

Неравенства Чебышева.

Первое неравенство Чебышева.

Пусть Х – случайная величина с конечным m_x 

(1)

Разобьем маршрут интегрирования на два непересекающиеся интеграла и воспользуемся свойством аддитивности интеграла.

так как подынтегральная функция неотрицательная, то получаем

. 

Следствие. Пусть Х ≥ 0  по одному из свойств математического ожидания  m_x ≥ 0  уравнение (1) перепишется в виде:

(2)

Второе неравенство Чебышева.

(в центрированной форме).

Пусть случайная величина Х имеет конечные m_x и 

. (3)

Заменим в (1) на , и заметим, что

Эти оценки являются грубыми, на практике применяются довольно редко, причем - достаточно большое.

2) Сходимость по вероятности. Определение. Последовательность случайных величин сходится к случайной величине Х по вероятности при n0 если (4)

Эквивалентная запись:

Более краткая запись:

Замечание 1. В частных случаях в качестве предельной величины может выступать и не случайная величина (например M[X]).

Замечание 2. Принято еще более краткое обозначение

.

Замечание 3. Сходимость по вероятности принципиально отличается от обычного понятия сходимости неслучайных последовательностей.

Пример 1. Рассмотрим следующую последовательность случайных величин , где закон распределения Х описывается таблицей.

Xn	0	1
P

1. Показать что

Так как

2) Можно ли утверждать что последовательность реализаций данной случайной последовательности сходящейся к 0 в обычном смысле.

Пусть {X_n} – последовательность случайных величин с конечными математическими ожиданиями и дисперсиями.

Для любого nN построим последовательность среднеарифметических

, 

получим последовательность Y₁,Y₂…Y_n.

Определение. Говорят, что к последовательности {X_n} применим закон больших чисел, если

(5)

Теорема Чебышева (закон больших чисел).

Пусть для последовательности {X_n} выполняется следующие условия:

1. попарно независима;

2. 

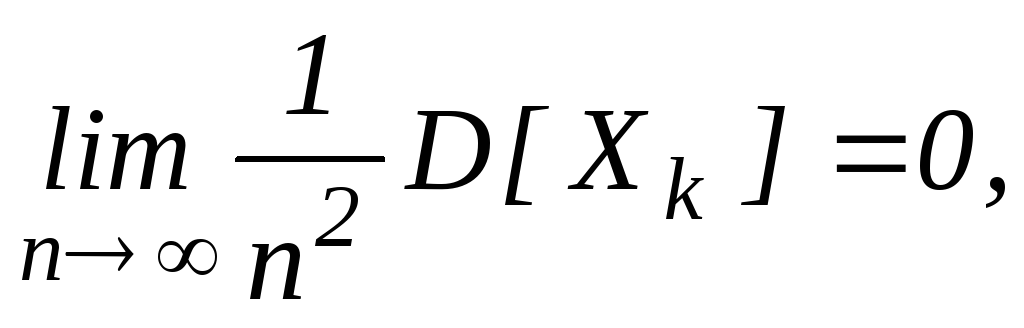
тогда для {X_n} выполняется закон больших чисел.

Для доказательства запишем уравнение (5). Согласно второму неравенству Чебышева в центральной форме:

Вычислим

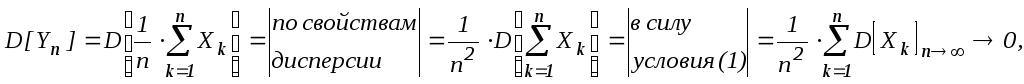что следует из условия (2) теоремы.

Используем достаточный признак сходимости по вероятности:

Замечание 1. Теорема Чебышева остается верной, если заменить по парную независимость на по парную некоррелированность.

Замечание 2. Условие некоррелированность так же можно снять, но тогда придется вводить условия более сложные для дисперсии (смотрите теорему Маркова).

Замечание 3. Имеют место следующие частные случаи проявления закона больших чисел:

1)

то есть дисперсии членов последовательности, равномерно ограничены  условие (2) выполняется;

2) все X_k попарно независимы, одинаково распределены и имеют конечную дисперсию  закон больших чисел формируется так:

Действительно,

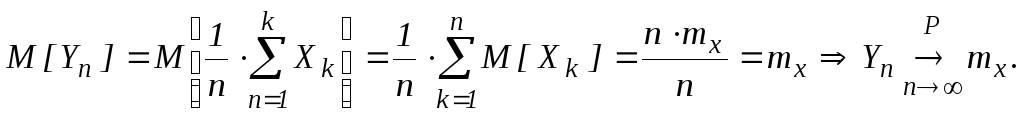
Теорема Бернулли.

Вводная часть.

Определение. Относительная частота успехов

Теорема Бернулли.

При увеличении числа опытов по схеме Бернулли относительная частота успехов

Р – вероятность успеха в одном опыте.

Обозначим I_k – индикаторы успеха в k-ом опыте. Очевидно, что I_k~B(1,P), kN. При любом n I₁,I₂…I_n – независимы в совокупности, а потому и попарно независимы. Условие (1) теоремы Чебышева выполняется.

, выполняется частный случай теорем Чебышева 

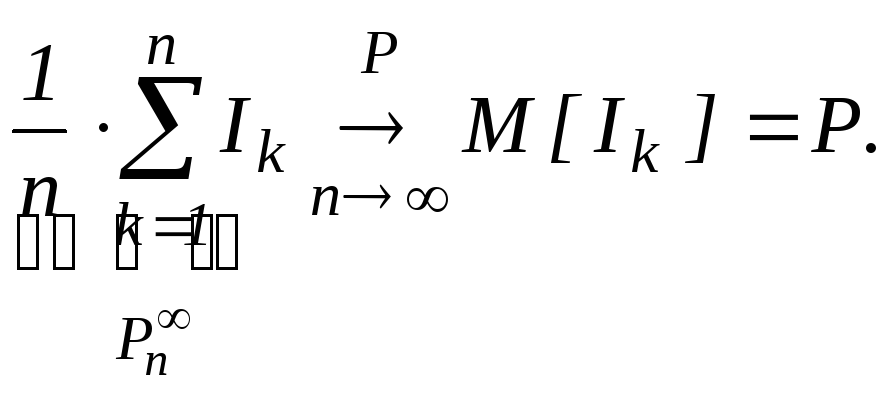
Пример 1. Пусть Х – число бракованных изделий из 100. За большой период рассчитано, что

а) в среднем брак составляет 1%;

б) известно, что ;

в) предположим, что модель брака удовлетворяет условию:

X~P_n(=1).

Во всех трех случаях оцениваем P{X ≥ 5}, где Х –число браков изделий из 100.

а) т.к. Х ≥ 0 и m­_x=1 по неравенству (1)

б) - известно 

в) (по таблице)