Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци21
.docЛекция 21
6.5. Проверка статических гипотез.
6.5.1. Общие понятия. Методика проверки.
Существуют два класса:
-
параметрические;
-
непараметрические.
Для проверки параметрических гипотез необходимо некоторые предположения о законе распределения генерального совокупности (как правило, используется нормальность генерального).
Для проверки непараметрических гипотез такие предположения не используются.
П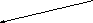
 роверка
гипотез.
роверка
гипотез.
о характеристиках или параметров генерального о законе распределения


сравнение с эталоном сравнение характеристик в
двух независимых генеральных
Алгоритм проверки.
-
Сформулировать основную гипотезу и альтернативную гипотезу.
Основная гипотеза
Н0
:а=![]() ,
,
![]() -
эталон,
-
эталон,
![]()
Альтернативная
гипотеза Н0 : а
>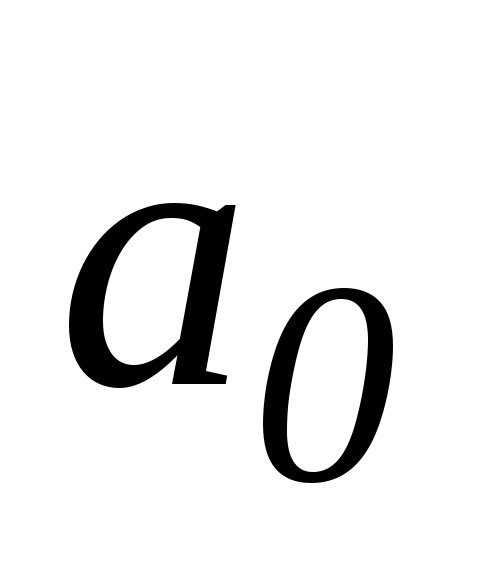 - правосторонняя,
- правосторонняя,
а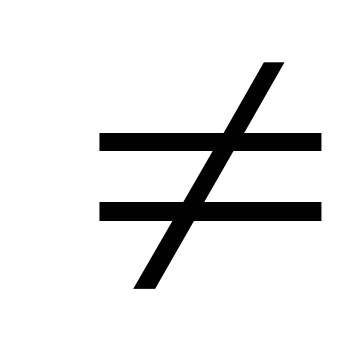
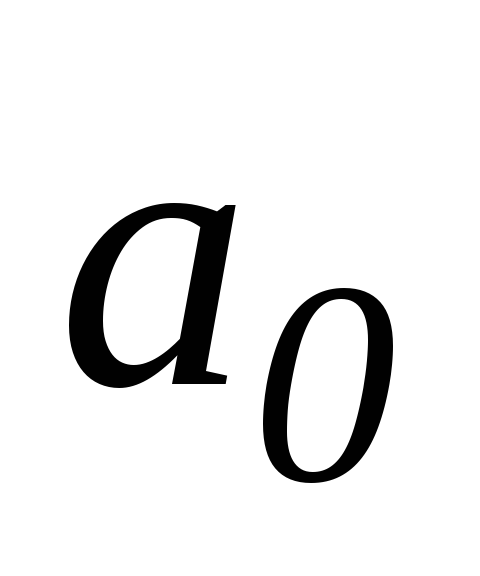 - двусторонняя,
- двусторонняя,
а <![]() - левосторонняя
альтернатива.
- левосторонняя
альтернатива.
-
Задать уровень значимости
 .
.
![]() ,
,
имеет смысл малой вероятности редко осуществимого события.
-
Выбрать подходящую статику:
-
должна быть удобной мерой расхождения между гипнотическим значением
-
далее не понял
-
закон распределения этой статики должен быть известен и по возможности не зависеть от неизвестного параметра. Различают простые и сложные гипотезы (основные гипотезы).
Определение. Простой называется гипотеза, полностью определяющая закон распределения статики.
Определение. Сложной называется гипотеза, не полностью определяющая закон распределения статики.
-
Пусть Z – подходящая статика, G – область значения статики Z. Разобьем множество G на две непересекающихся подобласти:
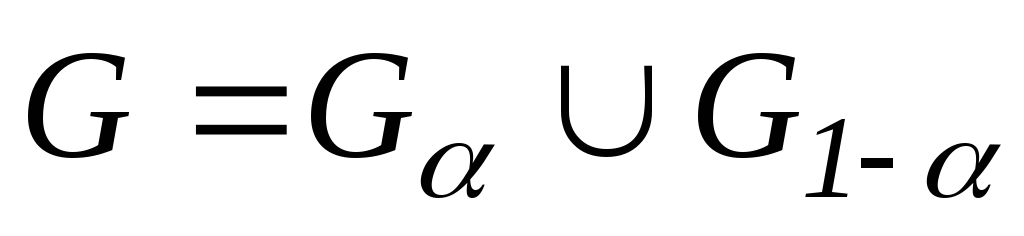 ,
,
![]() -
критическая область;
-
критическая область;
![]() - доступная область;
- доступная область;
![]() должна удовлетворять
уравнению:
должна удовлетворять
уравнению:
![]()
![]() (1)
(1)
-
Решающее правило:
Если Zвыб![]()
H0
– опровергается
как несоответствующее опытным данным.
H0
– опровергается
как несоответствующее опытным данным.
Если Zвыб![]()
следует принять H0
на данном
уровне значимости.
следует принять H0
на данном
уровне значимости.
(Опровергнуть всегда легче, чем принять.)
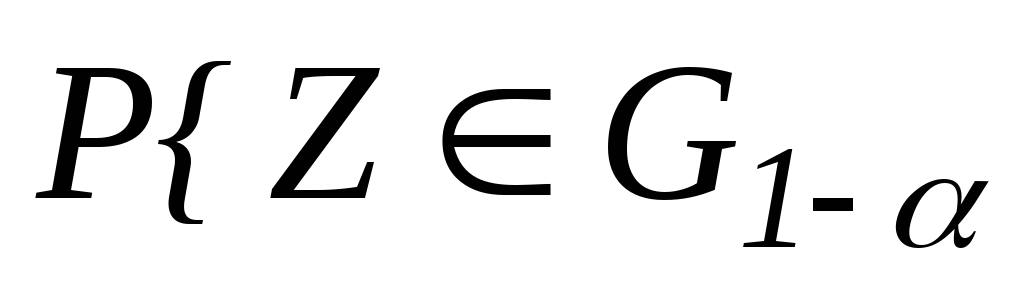
![]() (2)
(2)
Ошибка первого рода: «отвергнуть правильную гипотезу».
Вероятность этой ошибки равна .
Ошибка второго рода: «принять ложную гипотезу».
Вероятность этой ошибки равна .
Эти ошибки неравноправны, они ведут к разным последствиям.
Пример 1. H0 : цель своя, H1 : цель чужая
-
ошибка первого рода: ложная тревога сбивается своя цель;
-
ошибка второго рода: пропуск цели.
Возникает задача
оптимизации
при выборе критической области:
![]() -
фиксируется,
-
фиксируется,
![]() -
инициализируется.
-
инициализируется.
6.5.2. Выбор критической области в задаче сравнения с эталоном.
I вид распределения статистики: нормальный, Стьюдента и т.п. – асимметричный относительно начала координат.
Здесь график
II вид
распределения статистики:
типа
![]() -
распределения.
-
распределения.
Здесь график
Для математического ожидания.
Проверим: H0 : mX=m0

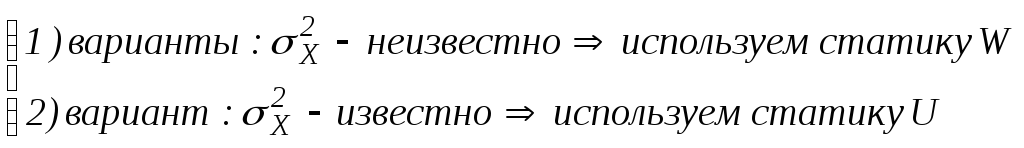
![]() ~N(0,1).
~N(0,1).
H0
:
![]()
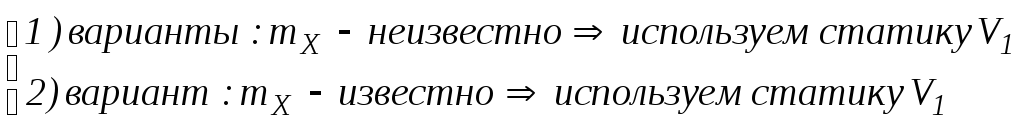
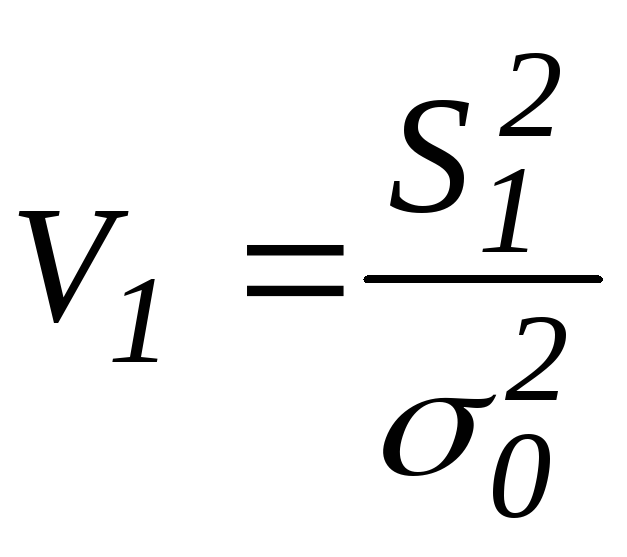 ~
~![]() .
.
Для Р:
![]() (3)
(3)
Пример 1.
Время реакции на световой сигнал среди
водителей-профессионалов должно быть
3сек.
для безопасной езды в темное время суток
(m0=3сек.).
Эксперименты над 16 водителями дали
следующие результаты:
![]()
-
Следует ли из этих данных, что время реакции испытуемых значимо больше номинального на уровне значимости
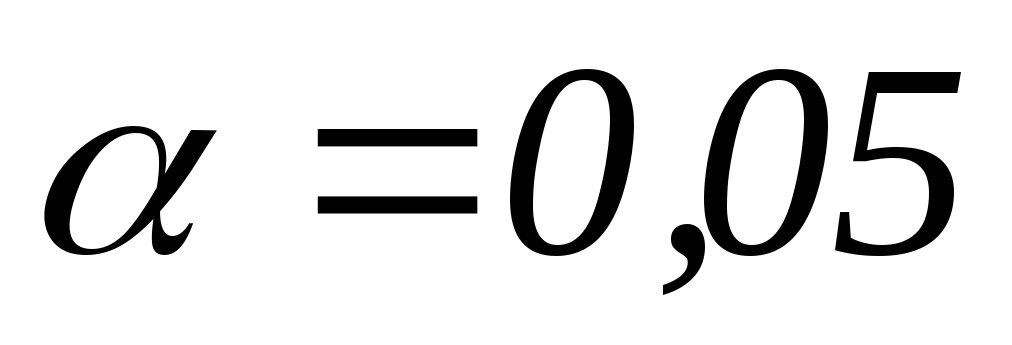 ?
? -
Что изменится если
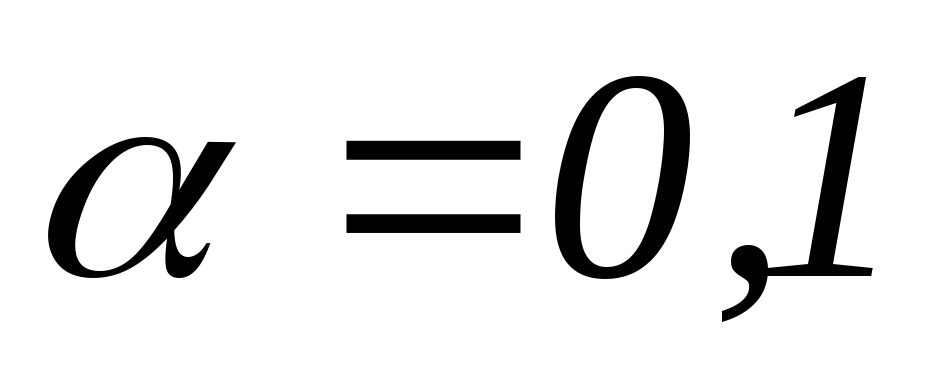 ?
? -
Что измениться если известно, что
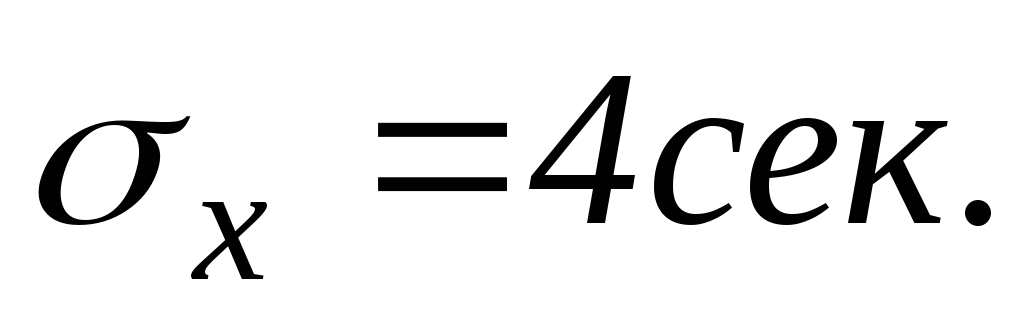 ?
? -
Можно ли считать, что время реакции водителя значимо отличается от номинального?
![]()
![]()
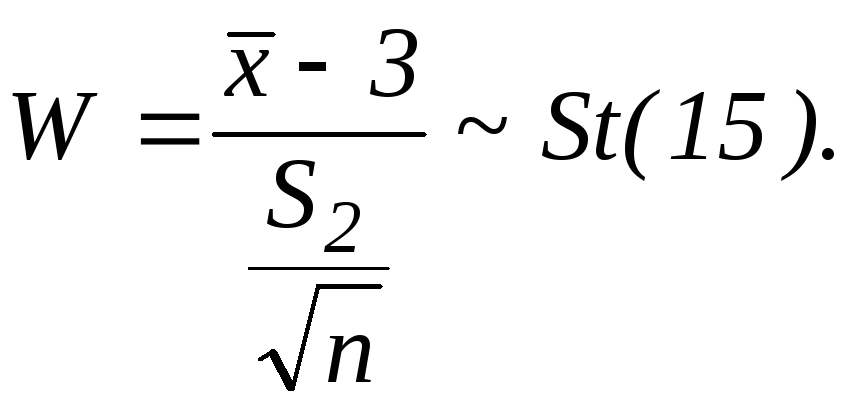
хреновый не разборчивый график
По таблице распределения Стьюдента находим квантиль:
![]()
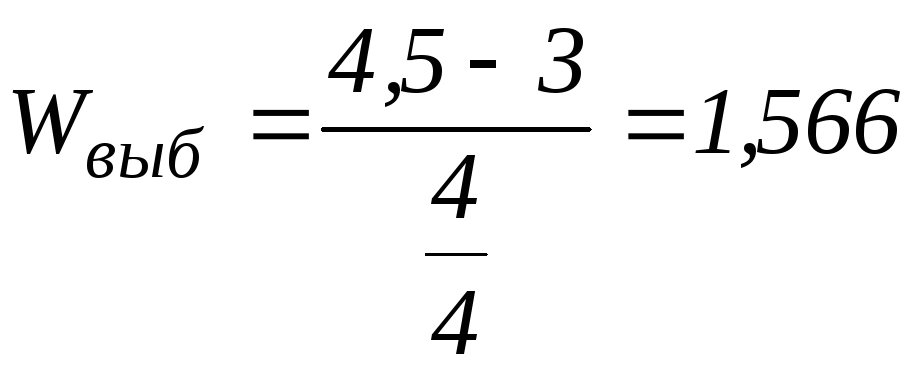
H0 принимается на этом уровне значимости
-
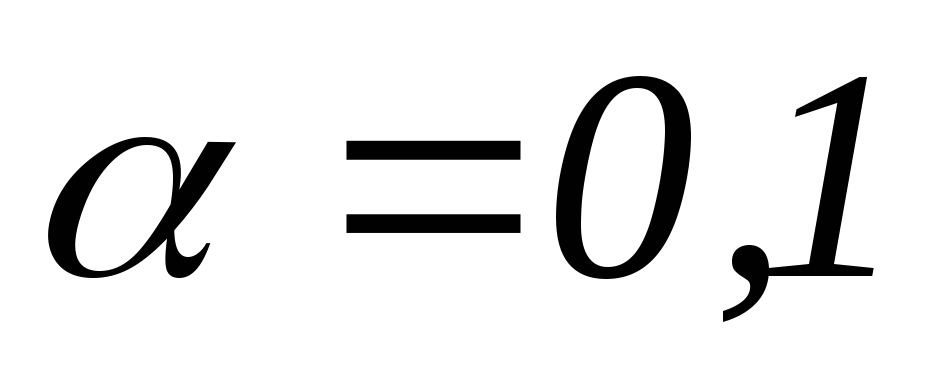 проверить что
H0
–
отвергается.
проверить что
H0
–
отвергается. -
Изменяется статистика и квантиль
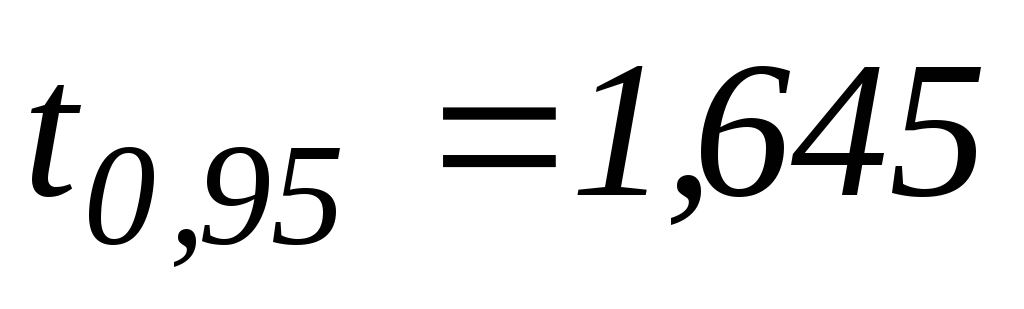 (из таблицы нормального распределения).
Приближается к 1,5.
(из таблицы нормального распределения).
Приближается к 1,5. -
Подстановка:
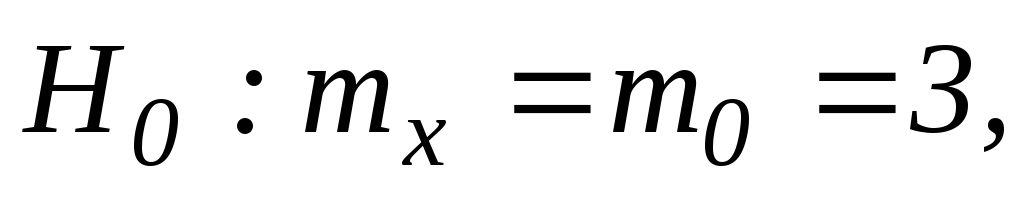
![]()
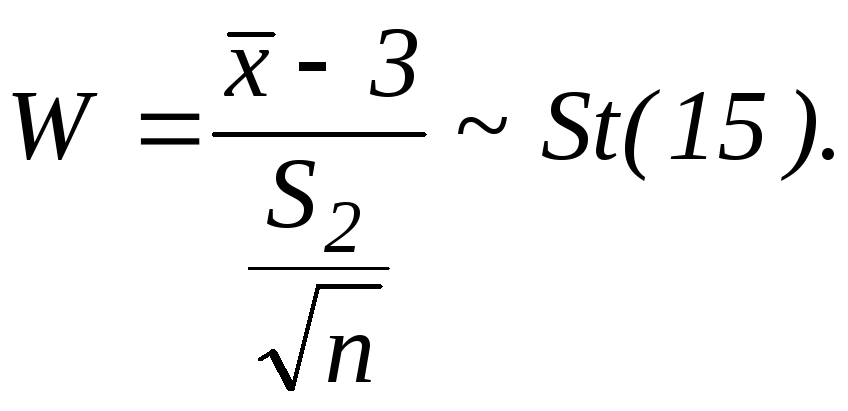
![]() подставится в H0
с большей степенью надежности.
подставится в H0
с большей степенью надежности.
![]()
Пример 2.
Р-
известная вероятность брака. Поставщик
утверждает:
![]() ,
заказчику необходимо
,
заказчику необходимо
![]() Полагаем
Полагаем
![]() для
обоих.
для
обоих.
-
Обследовано 400 деталей и обнаружено 16 бракованных
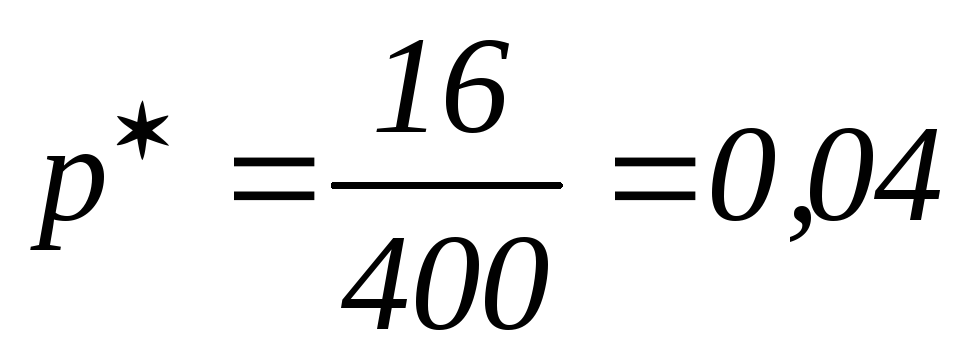
превышает 0,03
значимо или нет?
превышает 0,03
значимо или нет?
-
Какова вероятность принять партию, в которой 6% брака?
![]() В основе гипотезы
утверждается отсутствие эффекта, в
альтернативе присутствие эффекта.
(рисунок геморный)
В основе гипотезы
утверждается отсутствие эффекта, в
альтернативе присутствие эффекта.
(рисунок геморный)
-
если
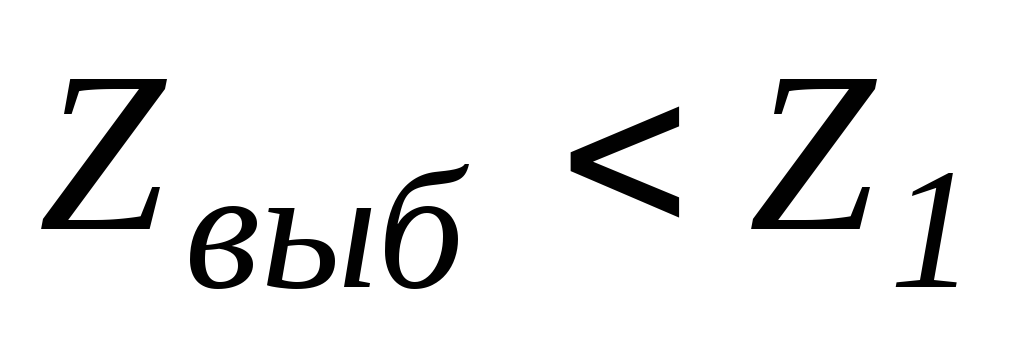 ,
то Н0
принимается;
,
то Н0
принимается; -
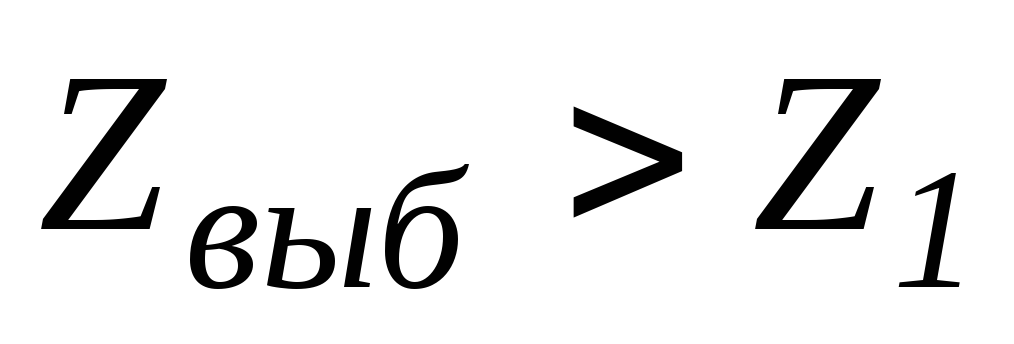 ,
Н0
отвергается;
,
Н0
отвергается; -
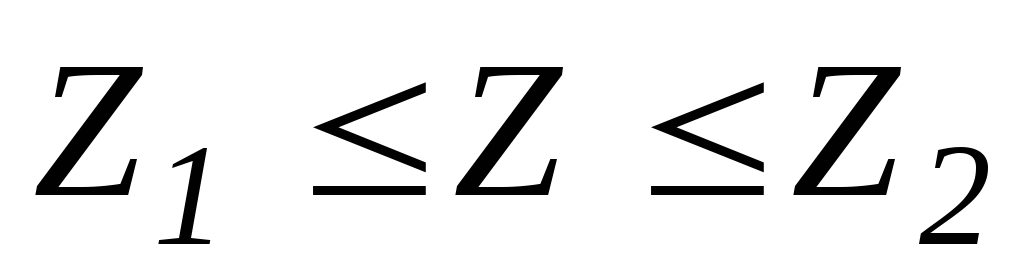 Н0
уже
отвергается, Н1
еще не
принимается.
Н0
уже
отвергается, Н1
еще не
принимается.